恶劣气象海况下船舶航线的多变量多目标优化建模

李明峰， 王胜正， 谢宗轩

(上海海事大学 商船学院， 上海 201306)

随着计算机和智能技术的不断发展，气象导航技术得到越来越多的关注。气象导航是指根据准确有效的天气和海洋预报及大洋气候资料，并结合船舶相关信息和航次信息等，为船舶航行设计出最佳的气象航线。[1]近年来，随着对能效的要求不断提高，航运业对气象导航的要求越来越高。在气象航线优化过程中，不仅要同时对航路和航速进行优化，而且要综合考虑油耗、航行时间和航行安全等多个目标。因此，气象航线优化是一种复杂的多变量、多动态约束、多目标问题。

在气象导航和航线优化方面，国内外学者开展了许多研究。传统的规划算法有：一方面主要基于Dijkstra和A*算法进行航线优化，例如：PARK等[2]以最低油耗为优化目标，先设定船舶航速恒定并使用A*算法调节航线转向点的位置，再结合几何规划法分配每个航段的航速，从而得到最优航线；JOO等[3]先采用A*算法调节航线转向点位置，并以气象数据为基础，采用Dijkstra算法优化每个航段的航速，而实际情况中航路与航速是相互依赖的，分段优化不是非常合理的方式。另一方面主要基于等时线、动态规划及其改进算法进行航线优化，例如：RAPHAEL等[4]以航行油耗最低为目标，基于气象预报图提出一种三维动态规划算法，该算法将船舶航行等效为多阶段决策过程，将航线等效为一组有限的航路点，在船速恒定的情况下，通过分配航路点和到达航路点的时间寻找最优航线；张进峰等[5]充分考虑船舶在大风浪中的风增阻、波浪增阻和失速特征，建立基于动态规划算法的近海船舶避台航线优化模型，在避让台风的前提下，得到航行距离的最短航线；LIN等[6]提出一种基于三维修正等时线法(Three-Dimensional Modified Isochrone,3DMI)的多动态影响因素的船舶航线优化法，采用浮动网格系统定义船舶航线优化的时空布局，建立优化模型，根据策略的不同，调整约束条件权重，寻找最优航线。然而，这些算法多假设船舶恒速或等功率航行，并没有涉及对每个航段航速的优化。

近些年，很多智能算法被应用到了航线优化中。例如： WANG等[7]提出一种实数编码遗传算法(Genetic Algorithm, GA)，用于寻找航行时间最短的航线，该算法根据个体在排序群体中的位置进行适应度分配，极大地简化了适应度值的计算，同时引入一种混合变异算子来增强对最优解的搜索并保持种群多样性；余文曌等[8]针对GA在路径规划中出现过多搜索冗余和收敛效率低等问题，提出一种基于弹性网格改进的GA，并将其应用到无人艇路径规划中；TSOU等[9]建立模拟生物体最佳行为的路径搜索模型，通过一个离散的网格系统和蚁群算法，以尽量减少燃料消耗和CO2排放量为目标，获得最优的航线；陈立家等[10]针对蚁群算法计算量大和寻优效率低下的问题，建立航线设计网络模型，并对蚁群算法进行改进，对信息素浓度进行人为控制，提出一种多约束条件下以航行综合成本最低为目的的最优航线生成算法；陈晓等[11]采用Maklink图和Dijkstra算法产生初始路径，减少蚁群算法的计算量，提高算法的寻优效率；赵化川等[12]结合船舶失速计算公式和船舶临界速度计算公式，分别建立航时最短、燃油最少的数学模型，并使用模拟退火算法分别求解。以上智能算法大多基于单目标进行航线优化，不能满足当前的需求。针对该问题,LI等[13]以航行时间和航行风险为对象建立模型，并采用非支配排序遗传算法-II[14](Non-Dominated Sorting Genetic Algorithm II，NSGA-II)求解，但该方法仅对转向点的位置进行优化设计，并没有对每一航段的航速进行分配。

本文基于现有气象航线优化方法存在的问题，提出一种多变量、多目标气象航线优化方法。该方法以船舶转向点位置和每个航段的航速为优化对象，以船舶特性和动态规避恶劣海况为约束条件，以航行时间和航行油耗为优化目标，建立多目标航线优化模型，并采用多目标遗传进化算法求解得到最优航线。

1 多变量多目标航行优化建模

1.1 模型变量定义

转向点位置(包括出发港与目的港)和每个航段的航速组成船舶的一条完整的航线，其中部分转向点要求航线必须经过(如港口以及大洋航路点)，这些转向点的地理位置信息是在航线规划初期就确定的，在算法迭代中不予调整，优化前的航线示意见图1。初始航线中包含有m个固定转向点，P=[P1,P2,…,Pm]，优化方法示意见图2。将固定转向点以大圆航线相连，每段大圆航段按等距离Δs进一步细分，在大圆航线上可得到n个位置已知的等分点，作为产生n个位置待优化转向点的基准点B=[B1,B2,…，Bn]，规定n个待优化的转向点X=[X1,X2,…,Xn]的位置调整只能限制在以基准点为垂足，垂直于当前大圆航段的一定距离h内，从而使每个待优化转向点的位置可由基准点位置计算得出，其中，Pi、Bi和Xi分别为第i个固定转向点、第i个基准点和第i个待优化转向点的位置向量。因此，船舶航线优化问题的变量为n个待优化转向点的位置X=[X1,X2,…,Xn]和m+n-1段航段的对水航速(vW=[vW1,vW2,…,vWm+n-1])共2n+m-1个决策变量，在得到这些变量值之后，连接待优化转向点和固定转向点即可得到一条优化航线。

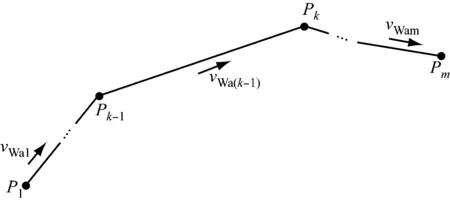
图1 优化前航线示意

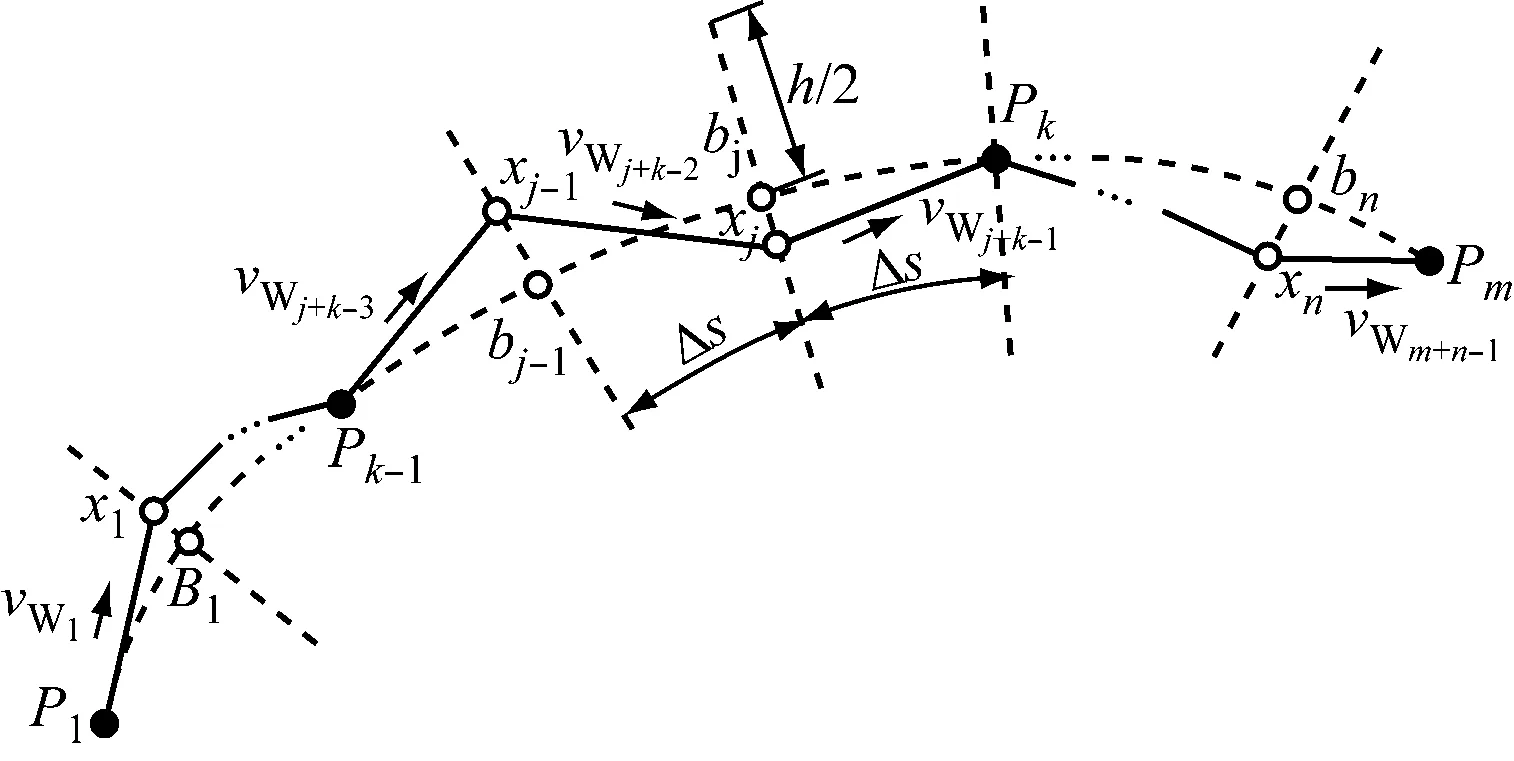
图2 船舶航线优化法示意

1.2 目标函数

本文建立以船舶航行的总油耗和航行总时间为优化目标的多目标函数：

(1)

(2)

式(1)和式(2)中:T为航行的总时间;G为航行总油耗;di为航线第i段的距离，为相邻两转向点位置的函数;vGi为第i段的对地航速;vWi为第i段的对水航速;g(vWi)为主机每日油耗，t/d;f(Hi，Wave)为浪高惩罚函数；N=m+n-1为航线的航段总数。

每个航段的对地航速vGi为对水航速vWi的函数式为

vGi=vWi-Δvi

(3)

式(3)中:vWi为第i段的对水航速;Δvi为第i段的航速损失。

船舶在海上航行时，其航速会较静水条件时减小，这种航速下降的现象称为船舶失速。船舶失速分为两种类型:

1) 由于风和波浪的扰动，在主机功率不变的情况下航速较静水条件时减小称为自然失速。

2) 船舶在大风浪中航行时，为减轻波冲击和剧烈摇荡引起的拍底、甲板上浪等危险现象而采取的有计划的降低航速称为有意减速[1]。计算船舶的速度损失[15]为

(4)

式(4)中:Δvi为第i段的速度损失;vWi为第i段的对水航速;Cβ为方向衰减系数，与船舶的遭遇角相关；CU为速度衰减系数，取决于船舶的方型系数和装载情况及弗劳德数Fr；CForm为船型系数。Cβ、CU和CForm的计算见文献[16]。

主机每日油耗的计算很多都采用经验公式计算，即

(5)

式(5)中:g为主机每日油耗;vWi为第i段的对水航速，kn;a、b、c和d为拟合系数。

1.3 惩罚函数

本文在建立的油耗和航行时间模型引入一个惩罚函数f(Hi，Wave)，其表达式为

(6)

式(6)中:Hi，Wave为航线第i段的平均浪高;Ht为航行中允许的最大浪高;K为值较大的惩罚系数。模型引入惩罚函数之后，在算法迭代的过程中，如果在随机产生的一条航线中的任一航段中，船舶在高于最大允许浪高的环境下航行，会得到一个较大的惩罚值，使该条航线的航行时间T和油耗G急剧增加，以致在算法的后续迭代中，该条航线最终被淘汰。相反，当航线中每一个航段的浪高都在允许的浪高下，航线的T和G的计算不会受到影响。因此，惩罚函数使得在最终规划出的航线的每个航段中，船舶始终在小于最大允许的浪高条件下航行。

1.4 模型约束条件

在实际的航行过程中，需要为模型添加以下几个约束条件：

1) 船舶的航速不能超过船舶设计的航速范围，即

vmin≤vWi≤vmax

(7)

2) 待优化转向点的位置必须限制于垂直于当前大圆航段的一定距离h内，即

(8)

式(8)中:Δdi为第i个优化点与基准点的距离。

2 多变量多目标优化问题求解

本文基于强度帕累托算法2(Strength Pareto Evolutionary Algorithm 2，SPEA2)求解模型，该算法是在多目标算法SPEA的基础上改进而来的,有关SPEA2算法的具体介绍见文献[17]。

2.1 初始种群的产生

本文采用实数编码，种群中每个个体代表出发港到目的港的1条航线，初始种群的产生包括产生每条航线的待优化转向点经纬度位置(X=[X1,X2,…,Xn]和航线上每个航段的对水航速vW=[vW1,vW2,…,vWN]。

航线待优化转向点的产生和计算见图3、式(9)和式(10)。

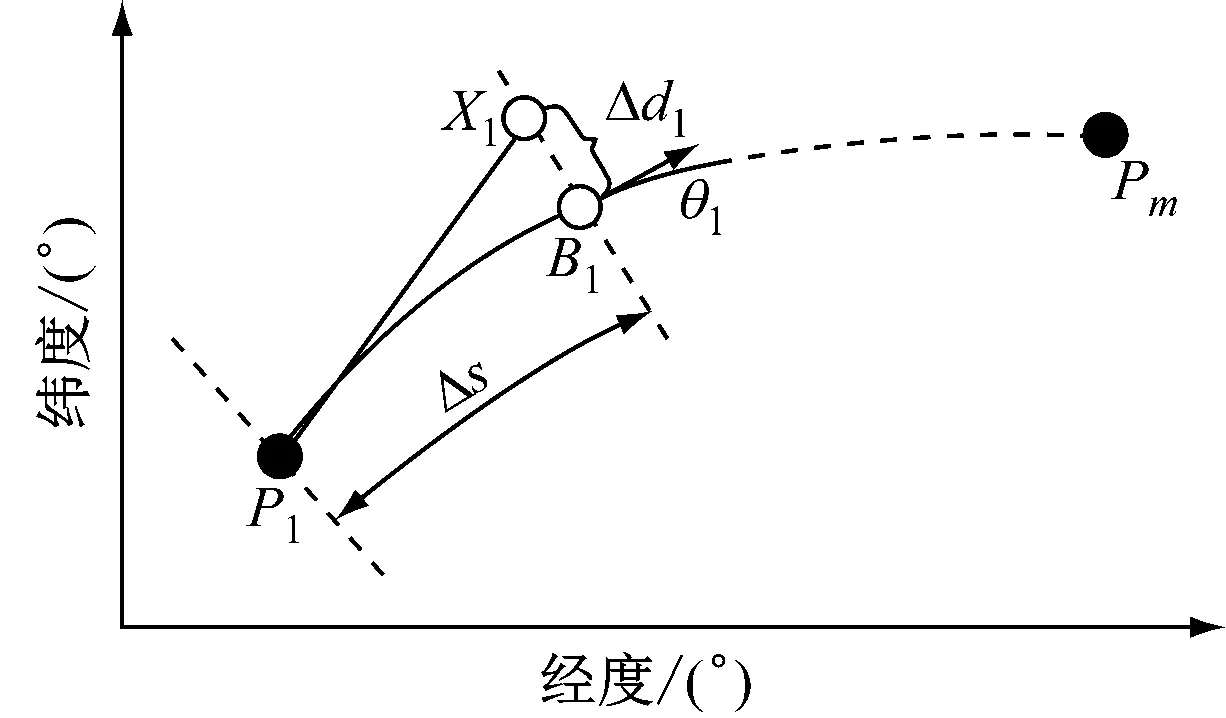
图3 航线待优化转向点产生示意

(9)

Δdi=(rand(1)-0.5)×h

(10)

式(9)和式(10)中：rand(1)为产生一个(0，1)的随机数；h为待优化转向点位置调整的最大范围。由式(9)和式(10)可知:要获得航线中随机生成的待优化转向点的位置，需要输入基准点的位置(B=[B1,B2,…,Bn])、待优化转向点与基准点的距离Δdi(正负号代表转向点位于大圆航段左侧还是右侧)和船舶在基准点的航向θi等3个量。

航线上每个航段的对水航速vWi的计算式为

vWi=rand(1)×[vmax-vmin]+vmin

(11)

式(11)中:vWi为第i段的对水航速；vmin和vmax为船舶允许的最小航速和最大航速。

2.2 基于浪高加权惩罚的适应度评估

种群中个体i的适应度计算式为

F(i)=R(i)+D(i)

(12)

(13)

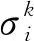
本文在计算T和G的过程中引入惩罚函数，当一条航线中任意一航段所在区域浪高高于最大允许值Ht时，通过惩罚函数给予航线的T和G一个较大的惩罚值，使得在确定支配关系时，具有较大T和G的个体(即航线)受到更多其他个体的支配。因此，该个体原始适应度值R增大，由式(12)可知，适应度值F也随之增大。在SPEA2环境选择中，对于适应度较大的个体，算法分两种情况处理：

1) 该个体无法进入档案集。

2) 在算法迭代前期该个体进入档案集，但随着算法的迭代，该个体逐渐被新产生的非支配个体取代。

档案集中每个个体代表的航线均未遭遇恶劣海况，且未受其他航线个体支配(原始适应度值为0)，具体算法流程见图4。

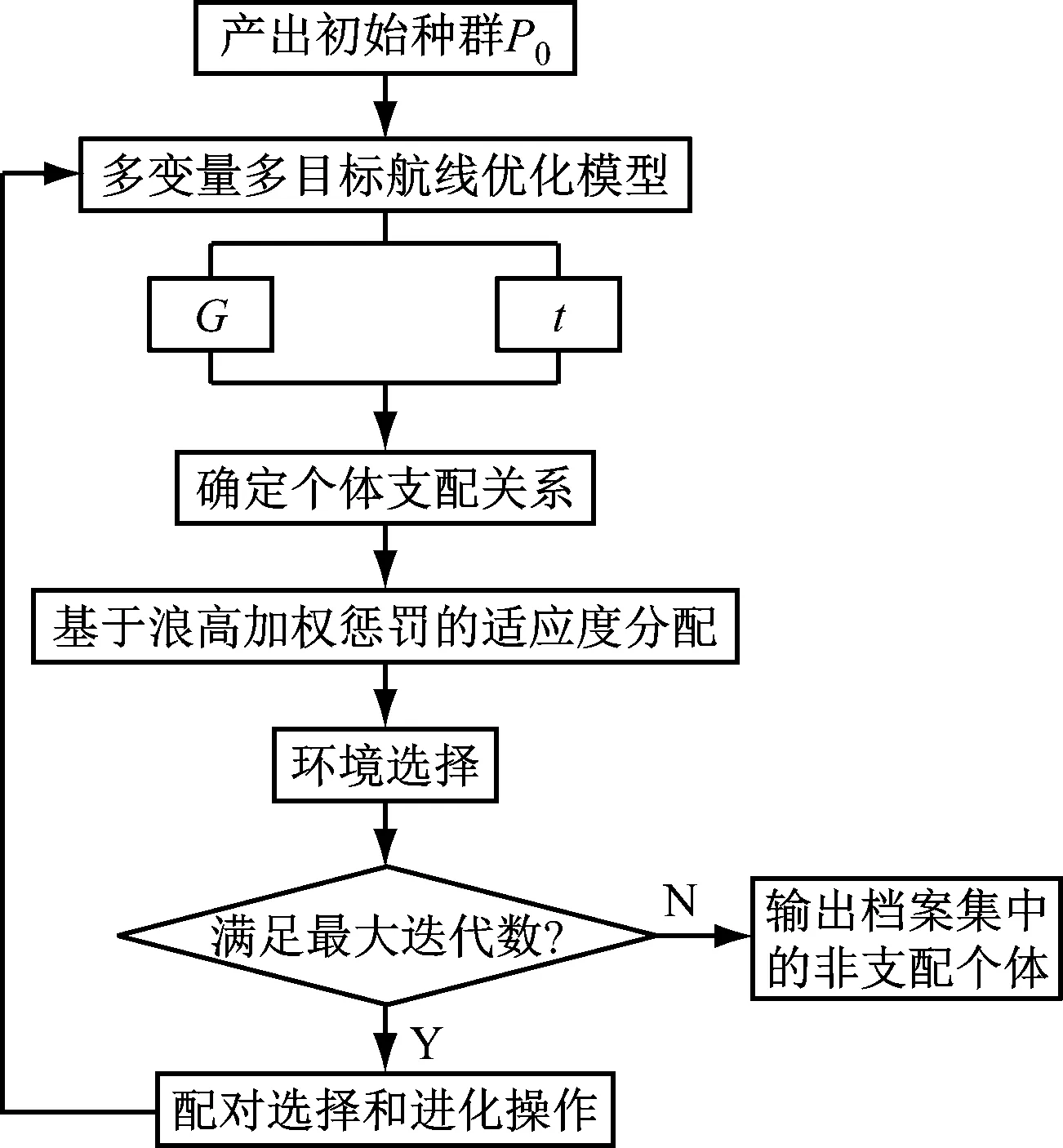
图4 多变量多目标航线优化流程图

3 试验分析

3.1 试验定义

为验证本文提出的优化方法的有效性，基于气象导航软件，将其应用到集装箱船舶航线规划中，初始航线为A与B两点之间的大圆航线，试验相关的参数见表1。

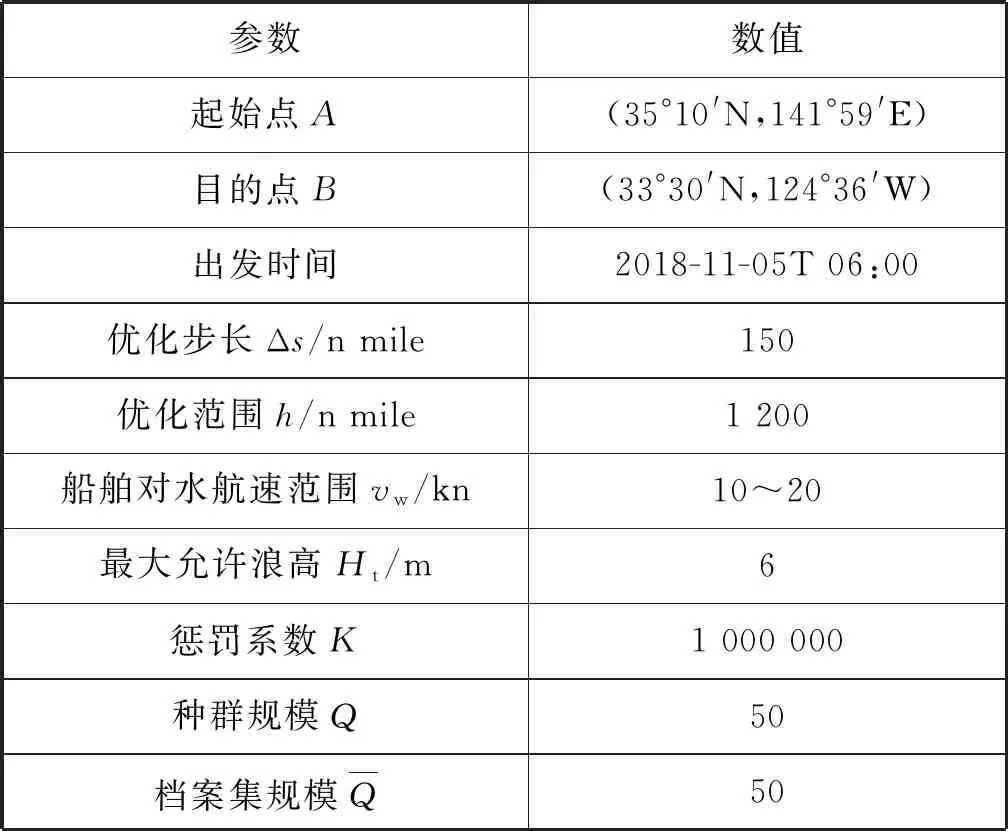
表1 试验相关参数设置

本次主要进行两个试验：试验1为验证根据本文提出的方法得到的航线在规避恶劣海况方面的效果，起点与终点之间的大圆航线作为对比对象，相关数据也在试验结果中列出；试验2为验证该方法在实现各种用户偏好下的航线优化效果，分别对采用本文提出的方法得到的最短航时航线、最低G航线和两点之间的大圆航线的进行对比分析。在两个试验中，设大圆航线的对水航速恒为15 kn。

3.2 试验1

A与B两点之间的大圆航线和在11月11日00:00的浪高分布见图5。由图5可知:船舶在11月11日00:00时刻已遭遇6 m以上的浪高，采用该方法优化出的航线与大圆航线对比见图6。在此次试验中，为更全面地了解动态变化的气象信息，气象软件在每天的00:00、06:00、12:00和18:00设置评估点，软件会自动获取评估点所在位置的浪高、风速等气象信息，两条航线每天06:00和18：00评估点位置及相应的浪高分别见7和图8，两条航线的整个航行过程中的浪高分布见图9。

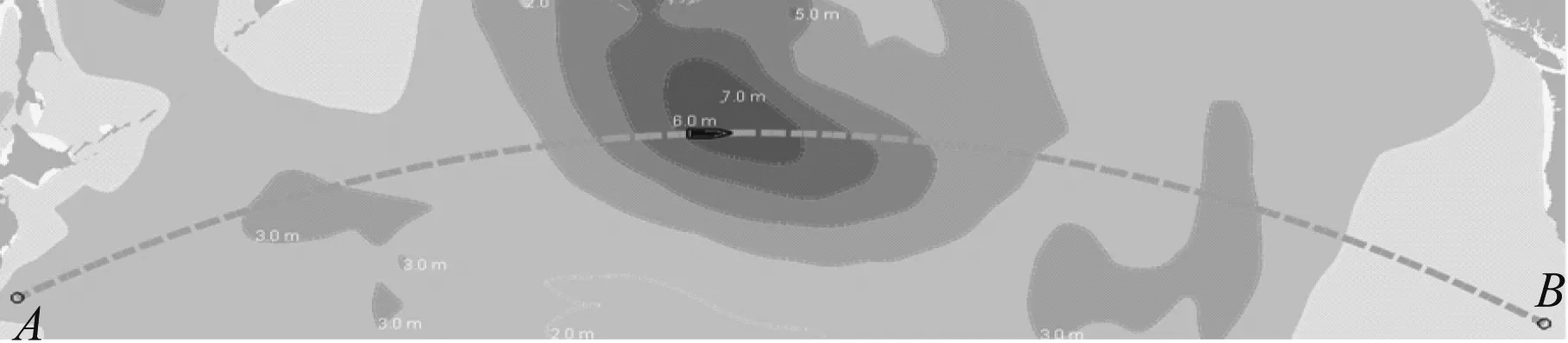
图5 2018-11-11T00:00浪高分布图

图6 大圆航线与优化航线

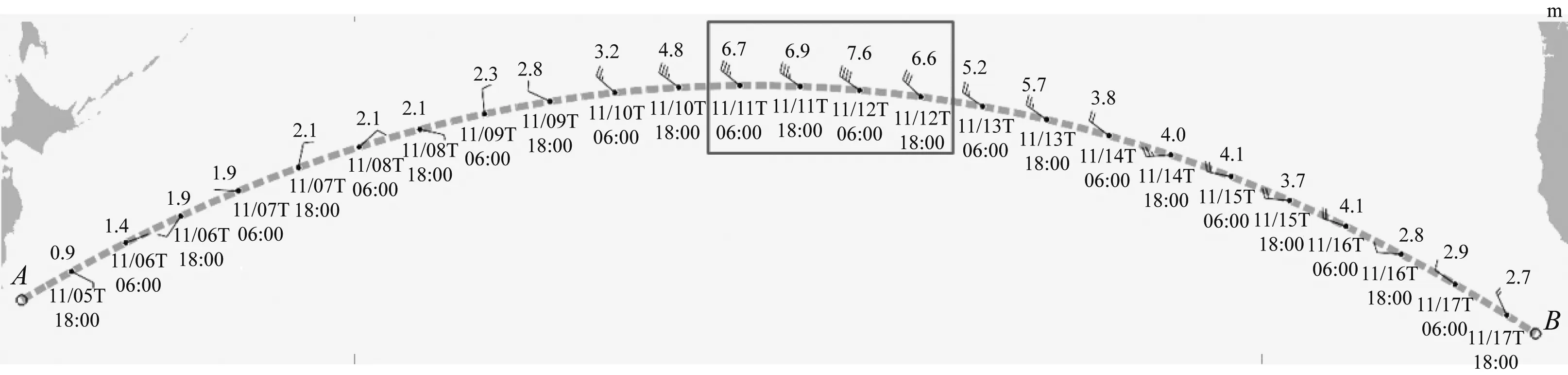
图7 大圆航线评估点浪高

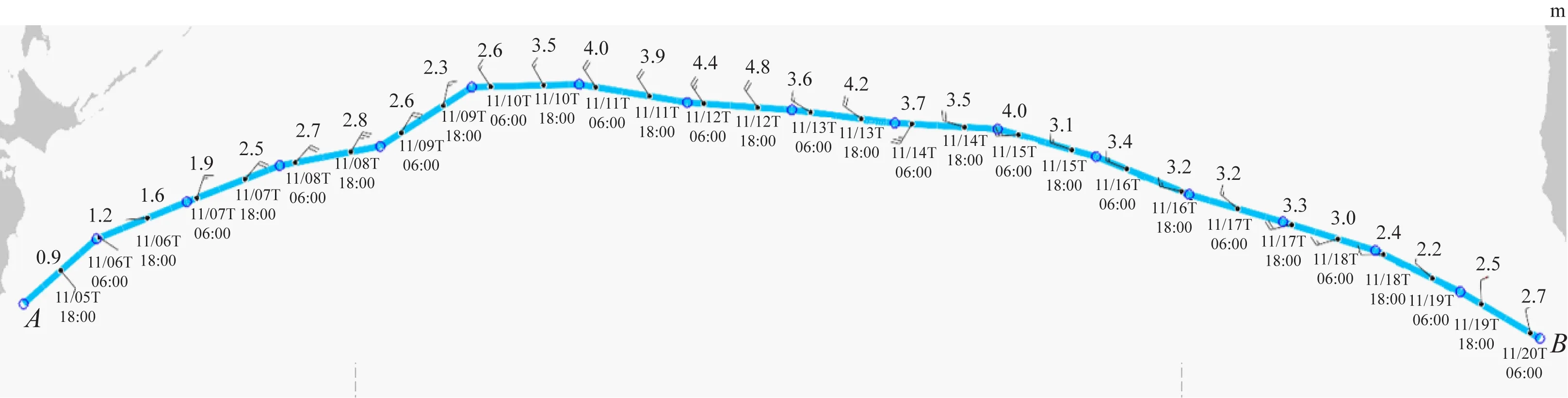
图8 优化航线评估点浪高

图9 浪高分布

优化航线经历的气象条件整体上比大圆航线好如见图9所示，且大圆航线经过高浪区域如见图7所示，仅统计每天06:00和18:00时刻的浪高信息，大圆航线在11月11日的06:00和18:00及11月12日的06：00和18:00分别遭遇浪高为6.7 m、6.9 m、7.6 m和6.6 m的海浪，在该海况条件下航行，船舶的安全性受到严重威胁，但通过该方法优化得到的航线并未遭遇高于6 m的海浪(见图8)。图8中:航线最高浪高仅为4.8 m，因此优化航线通过调整转向点位置和每航段的对水航速，有效避开航行过程中浪高高于6 m的恶劣海况区域。

3.3 试验2

本文提出的优化方法可根据用户的偏好优化，SPEA2算法输出的是一个帕累托解集，解集中均为非劣解，如果用户需要的是T最短的航线，可接受相对较高的G，只需要按航行时间升序对帕累托解集中的航线进行排序，第1条航线即为最短航时航线。同样，如果用户需要航行G最低，只需要按航线G升序排序，第1条航线即为最低G航线。根据本文提出的方法得到的最低G航线、最短T航线和两点之间的大圆航线见图10,3条航线的相关数据对比见表2。

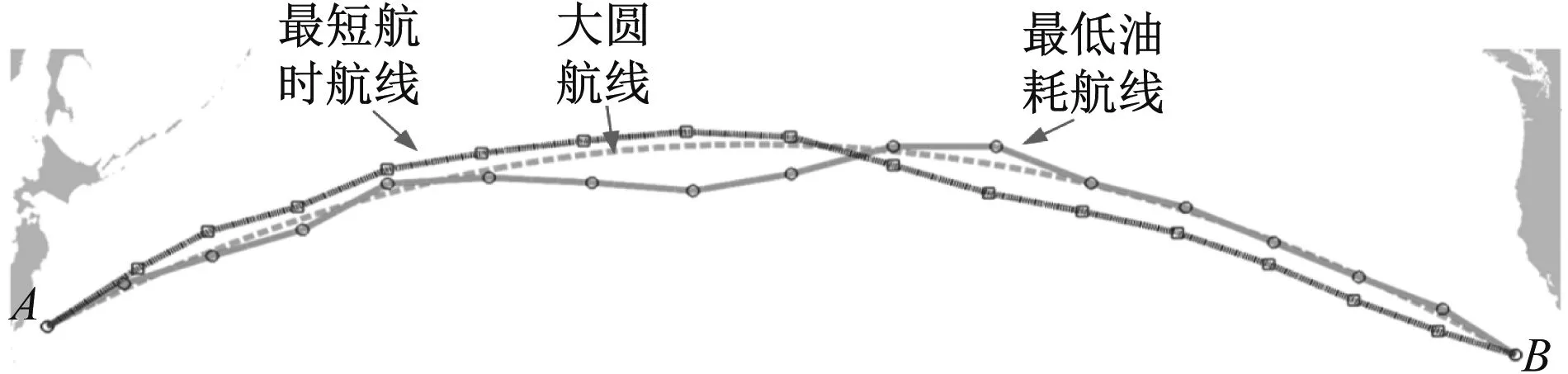
图10 根据用户偏好的优化航线对比

由表2可知:最低G航线和最短T航线的距离相比大圆航线分别增长1.3%和0.7%，差距不是特别大，说明该方法更倾向于调节每个航段的航速来优化航线，相比大圆航线，最低G航线的G下降了27.3%，T却延长了11%，而最短T航线在t下缩短12.8%的同时，G增加了27.3%，最低G航线、最短T航线和大圆航线的航段油耗见图11a(试验中的大圆航线以基准点划分每个航段)，最低油耗航线、最短航时航线和大圆航线的航段对水航速见图11b。由图11可知:较高的航速会导致油耗增加，最低油耗航线的船舶航速整体较低，导致t增加；最短航时航线为缩短t，整体的航速较高，导致航线总G增加，这与实际情况相符合。

表2 航线数据对比表

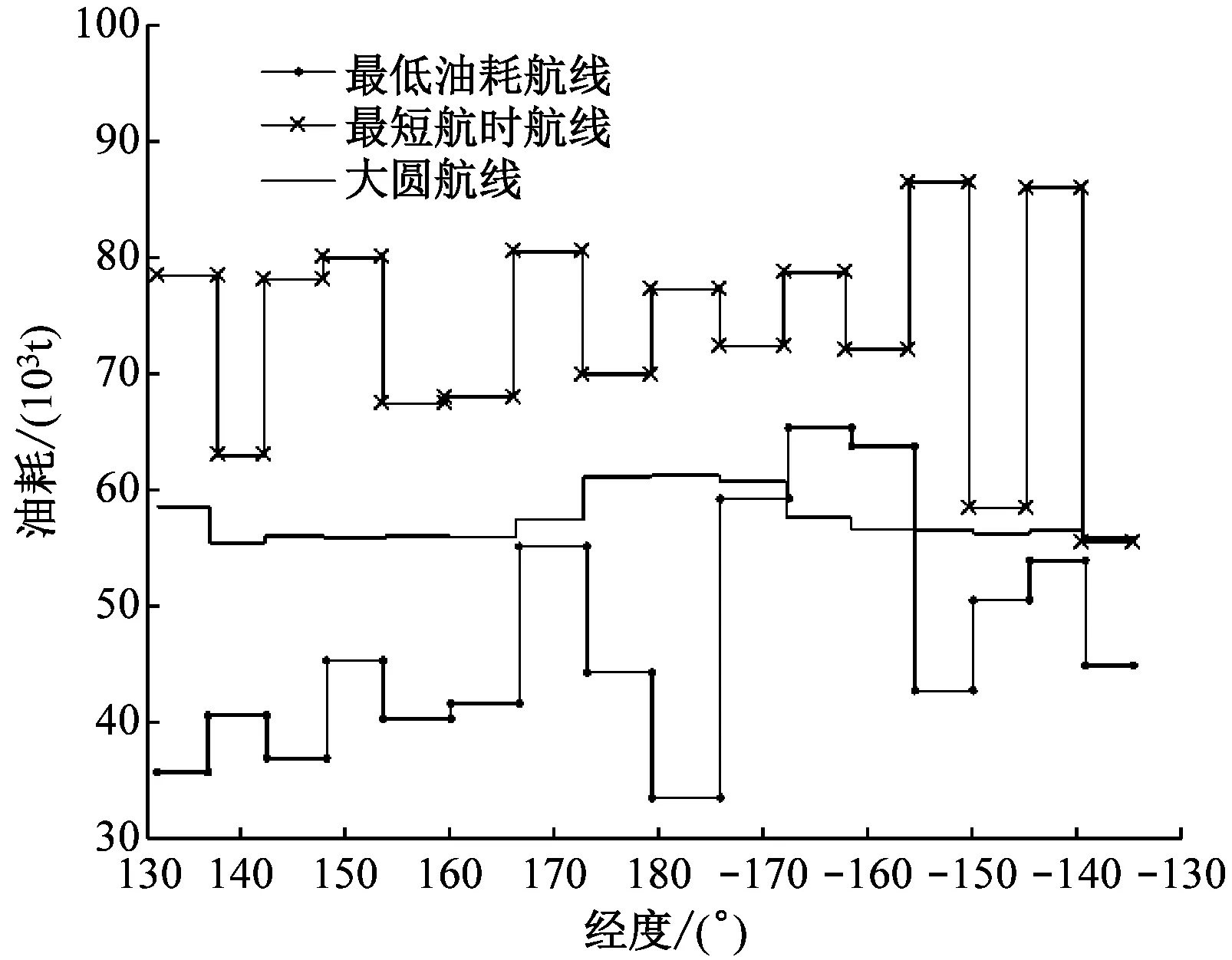
a) 航段油耗

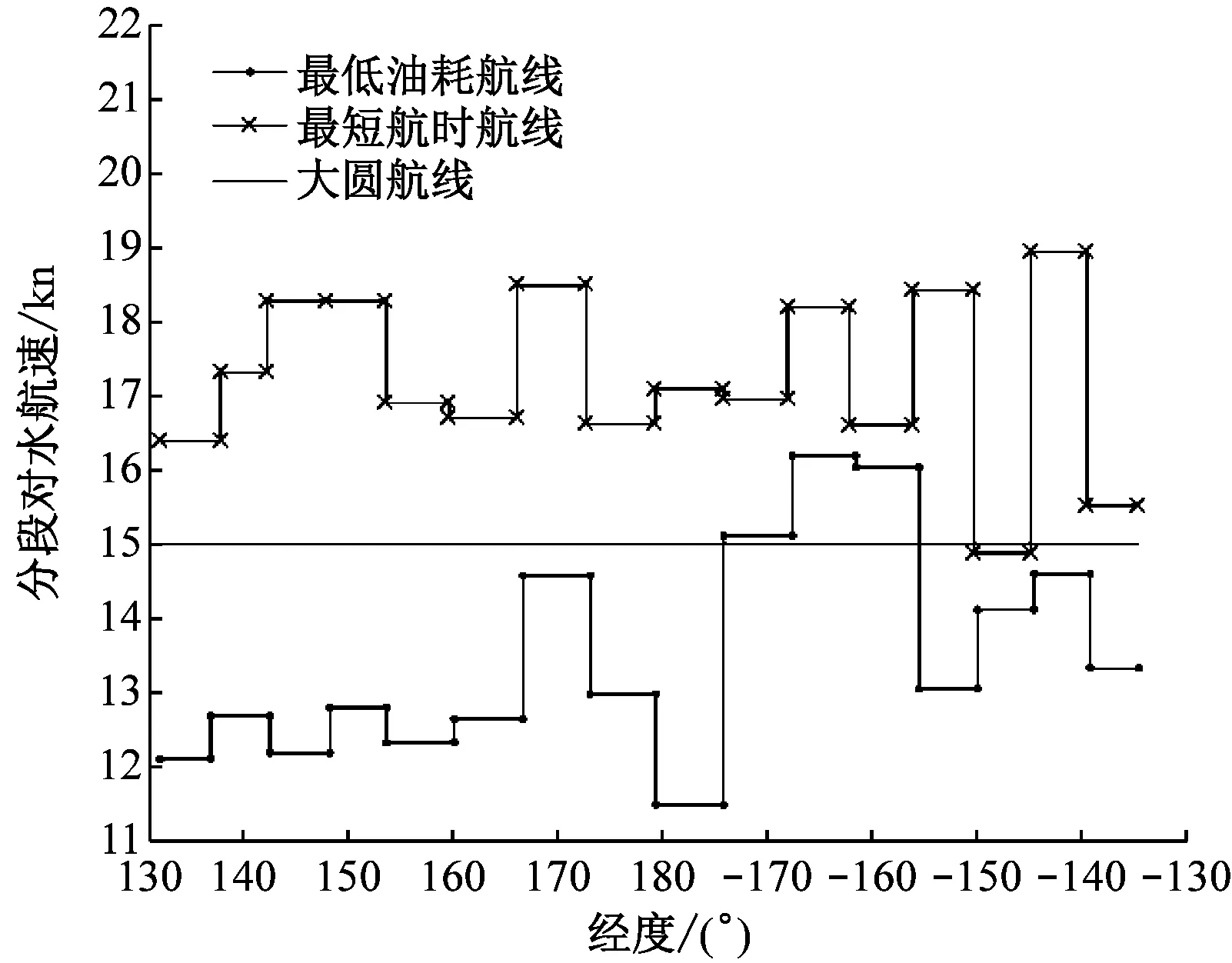
b) 航段对水航速

4 结束语

为满足航运业对气象航线优化提出的航速航路同时优化、综合考虑多个目标的要求，本文以G和T为优化目标，以航线转向点位置和航段航速为优化对象，以船舶特性(船舶最大最小航速)和规避恶劣气象条件为约束，建立多变量、多目标优化模型，并进行应用。试验1证明本文提出的优化方法能通过调节转向点位置和航段对水航速有效避开恶劣海况区域;试验2证明该方法可根据用户的偏好，选择最低油耗、最短航时的优化航线。

本文在气象条件中仅考虑浪高，在后续工作中，还会考虑洋流、风速和涌浪等更加丰富的气象影响因素，并在规避恶劣区域的方法上施加安全距离，以确保与危险分离，保证船舶航行的安全性，同时修改模型目标函数，得到船舶航行其他指标的优化航线。