能见度对天体观测高度的影响
吴 明, 常志远, 李 超, 徐轩彬
(1. 海军大连舰艇学院, 辽宁 大连 116018; 2. 武警海警总队机动第二支队, 浙江 宁波 315000; 3. 中国人民解放军91278部队, 辽宁 大连 116041)
天文定位是一种自主的导航方法,具有观测设备简单、廉价,不受人工或自然形成的电磁场干扰,不向外辐射电磁波和隐蔽性好等特点。因此,即使如今航海科技已十分发达,天文定位在应急航海和军事航海领域仍具有不可忽视的作用。[1-4]
虽然天文定位具有独特的优势,但其缺点也十分显著,例如实际使用中易受天气条件的限制。在采用六分仪观测或星图识别等方法获取天体高度时,需以水天线作为基准进行测量[5-6],当能见度小于理论视距时,水天线位置及其清晰度会有所变化,测量出的天体高度会产生一定的误差。目前,航海领域还没有考虑能见度影响的天体观测高度修正方法。本文针对该问题,先推导能见度对天体观测高度影响的理论修正计算式,在此基础上,考虑地面折光差的影响,给出能见度影响的实际修正计算式。此外,将该方法应用到太阳高度观测中,验证其有效性。
1 天体高度观测和修正的基本方法
地平坐标系见图1。图1中:从测者真地平圈算起,沿着天体方位圈度量到天体中心的大圆弧距h称为天体高度。[7]海上天文定位的关键步骤之一就是测量天体高度。

图1 地平坐标系
获取天体高度的传统方法是将水天线近似看作测者真地平圈,见图2。利用六分仪测量天体和与天线之间的弧距,得到天体的六分仪高度。

图2 航海六分仪的光学原理
在采用六分仪观测天体高度过程中,将水天线近似看测者真地平圈的位置,同时天体高度还受测者眼高、地球表面大气密度天体半径等因素的影响。因此,对观测到的六分仪高度进行一系列修正之后才能得到天体真高度,这些修正包括折光差、眼高差、视差和半径差等4种误差。[8]
在理想情况(能见度大于理论视距)下,采用该方法可得到具有一定精度的天体高度观测值。但是,当能见度小于理论视距时,水天线位置的高低会随着能见度的变化而变化。因此,在观测天体高度时,还应考虑能见度的影响。
2 能见度对天体高度观测的影响
2.1 海上能见度
海上能见度是指在人的正常视力范围内能看清海上最远目标轮廓和形状的最远距离,即能将目标的轮廓从天空的背景中分离出来的最远距离。海上能见度一般划分为0~9等10个等级,见表1。
目前,确定大气能见度的方法主要有仪器测量法、数字图像处理法[9]和人工目测法等,其中:
1) 天体仪器测量法使用大气透射仪和激光能见度自动测量仪等获取能见度,成本较高,难以在航海中推广使用。
2) 数字图像处理法通过拍摄影像,分析影像的对比度和饱和度等信息来获取能见度,已应用在海上能见度的测量中[10],该方法成本低、安装便捷,具有一定的应用前景。

表1 海上能见度等级
3) 人工目测法不需要在船舶上增加专门的测量设备,与导航雷达等测距设备配合,即可估算海上能见度,虽然观测精度略低,但其仍然是航海中最常用的能见度估算方法。
2.2 能见度对天体高度观测的影响
舰船在海上航行时,在理想条件下,测者能看到的最远距离为水天交界线,称为水天线。能见度对水天线的影响见图3。图3中:R为地球半径;e为观测者眼高;O点为地心;A点为观测者眼高位置;AE连线与地球表面相切于E点;BE为观测者到水天线的球面距离,称为理论视距。当能见度大于理论视距时,观测者能看到的水天线位于E点;当能见度小于理论视距时,观测者能看到的水天线位于C点。
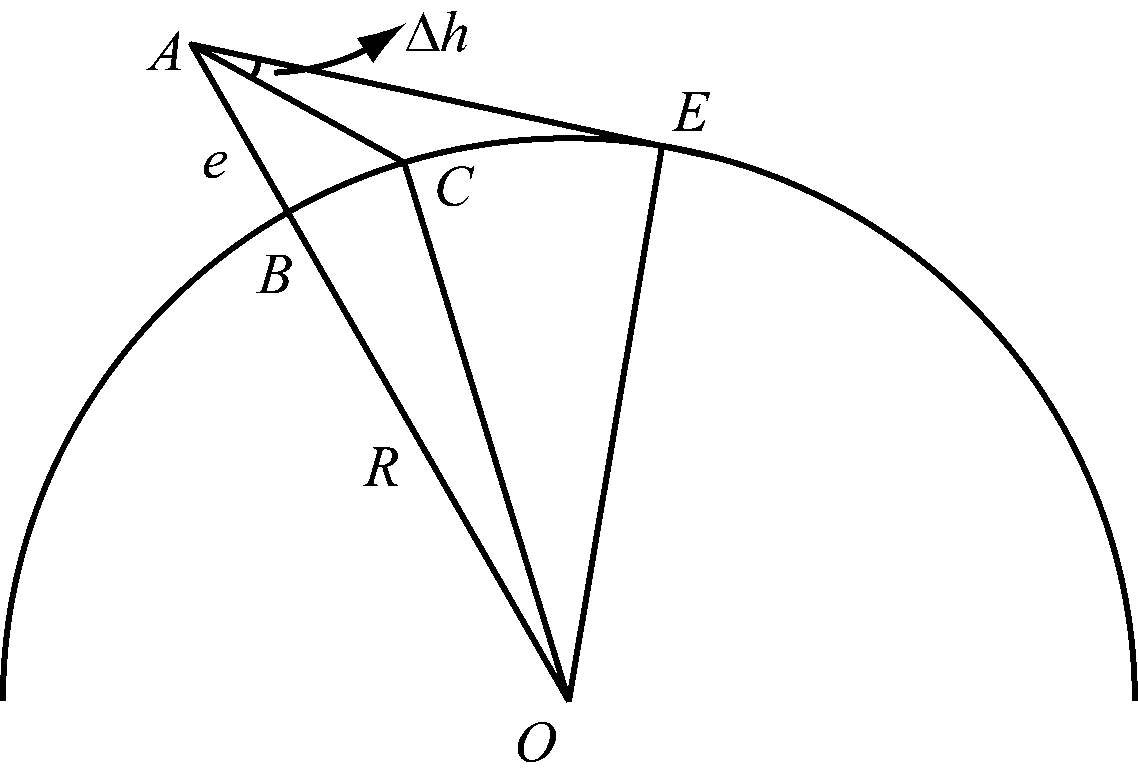
图3 能见度对水天线的影响
当能见度大于理论视距时,测者可看到清晰的水天线,因此不需要对观测高度进行修正;当能见度小于理论视距时,测者的能见距离为BC,观测时只能以C点为水天线,在这种情况下,采用六分仪观测天体高度,选取的水天线位置要比实际水天线位置低。因此,在该条件下测得的天体高度要比理想条件下的测量值大,此时观测到的天体高度需要修正Δh,Δh的计算方法如下。
1) 在△AOE中,有
(1)
2) 在△AOC中,由于观测者e相对于R为小量,因此令海上能见距离BC≈AC=λd,根据三角形余弦定理,有
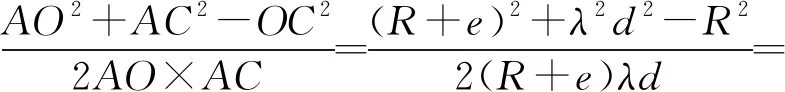
(2)
Δh=∠OAE-∠OAC=
(3)
式(2)和式(3)中:R为地球半径,m;e为观测者眼高,m;d为海上能见距离,n mile;λ为n mile与m之间的转换系数,通常取λ=1 852。式(3)采用所得结果为理想状态下的太阳高度能见度修正,是不考虑大气密度影响得出的修正值。
2.3 地面折光差影响修正
地球表面处于大气层的包围中,且大气密度随着高度的增加而逐渐变小,当光线穿过不同密度的大气层时,传播路径是向下弯曲的,会发生折射。地面折光差见图4。由于大气的折射作用,稍远于切点C的C′点光线按C′DEFGH方向进入观测者的眼睛,观测者的视距变远。

图4 地面折光差
C′点的真方向AC′与其视方向AT之间的夹角(称为地面折光差,又称蒙气差)。地面折光差γ越小,实际视距就越小;反之,实际视距越大。γ可表示为
γ=0.5KD
(4)
式(4)中:D为观测者与物标之间的距离,m;K为地面折光差系数,根据中国《航海表》中的眼高差表取K=0.16。
考虑γ后,实际太阳高度能见度修正计算式为
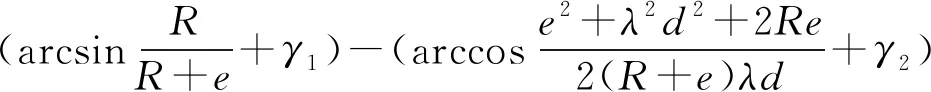
(5)
将式(3)和式(4)代入式(5),得
(6)
为航海上使用方便,将式(6)编算成表(见表2),查表引数为e和d。表2中:横线部分为能见距离大于理论视距的情况,不需要修正。在实际使用表2时,若查表引数位于表列引数之间,可采用线性内插法获取修正量。

表2 能见度影响的修正量 角分
由表2可知:天体观测高度因能见度而产生的修正量始终为正值;在观测者e不变的情况下,海上能见距离越大,天体观测高度修正量越小;在海上能见距离不变的情况下,观测者e越高,天体的观测高度修正量越大。
3 实际应用
为验证本文所述方法的有效性,进行2种d(4 n mile、3 n mile)、3种e(8.1 m、18.9 m、21.6 m)共计6种情况下的海上太阳高度测量,测量值与太阳真高度的绝对误差即为能见度引起的实测高度修正值。
采用人工目测法获取观测时的海上能见度,选取航行海区水天线附近的船舶或岛屿作为参考,通过与导航雷达回波显影相比较判断当时的能见度,精度约为0.5 n mile。在实测中,e的改变是通过在船舶不同层甲板上观测实现的。在不同e和不同d条件下观测的结果见表3~表8。

表4 太阳高度观测数据2(d=4.0 n mile, e=18.9 m)

表5 太阳高度观测数据3(d=4.0 n mile, e=21.6 m)

表6 太阳高度观测数据4(d=3.0 n mile, d=8.1 m)
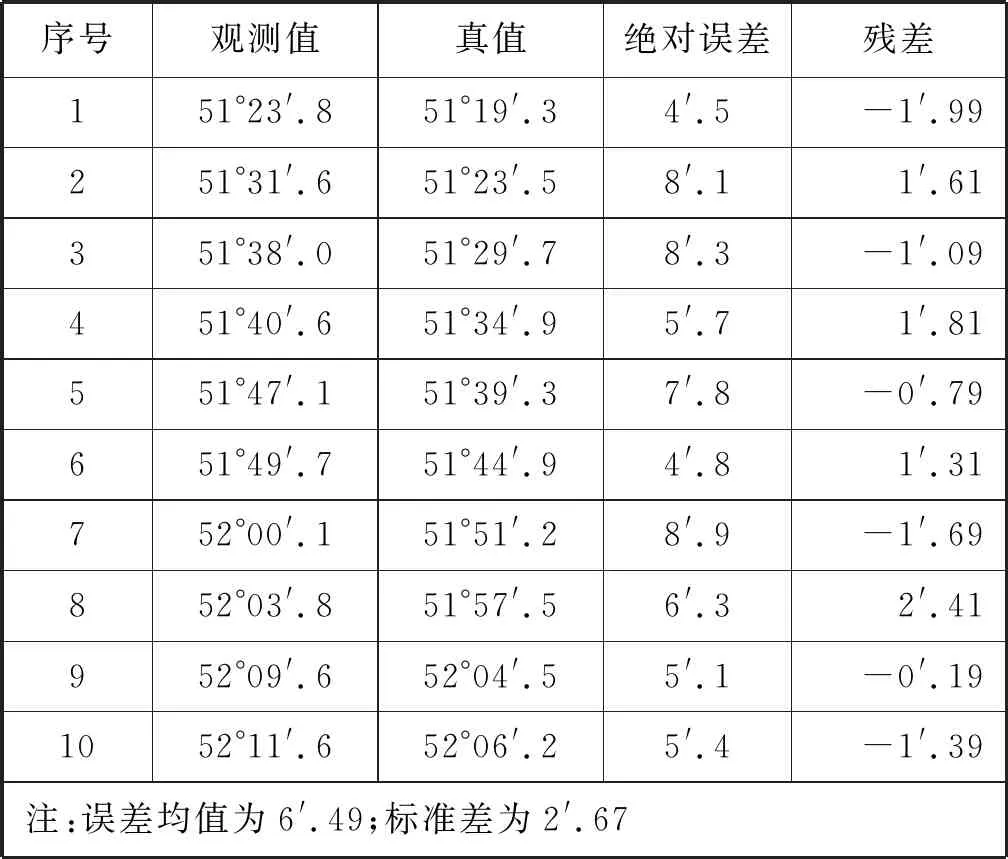
表7 太阳高度观测数据5(d=3.0 n mile, e=18.9 m)

表8 太阳高度观测数据6(d=3.0 n mile, e=21.6 m)
对实测数据进行误差分析,并将计算的高度修正值与实测修正值相比较,结果见表9。由表9可知:前3组数据符合较好,后3组误差略大,这是因为在观测后3组数据时,能见度约为4 n mile,此时水天线的清晰程度尚可,而观测前3组数据时,能见度约3 n mile,此时水天线比能见度为4 n mile时模糊,观测的难度增大,观测的误差有所增大。从观测误差的标准差来看,后3组数据的标准差明显大于前3组数据,这也是由于能见度的远近影响水天线的清晰程度,导致观测误差的稳定性变差。

表9 实测误差值与本文修正值的比较
由以上分析可知:
1) 观测高度修正量计算值与海上实测修正值相符,采用该方法可提高能见度小于理论视距情况下的太阳高度观测精度。
2) 当e一定时,能见度越差,修正的效果越差。因此,采用该方法修正时应注意,在能见度较差的情况下,采用本文提出的修正方法得到的结果也会存在一定的误差。
3) 当能见度一定时,随着e的增大,观测高度修正量会有所增大,根据这个特点,当无法准确判断能见度时,可通过降低e(在较低的甲板观测)来减小观测高度的误差。
4 结束语
本文开展的能见度对天体观测高度的影响研究,有助于对天体高度观测误差修正方法进一步完善,为能见度小于理论视距情况下的天体高度观测修正提供定量依据,从而降低能见度条件对天文定位的限制,使各种依靠水天线进行天体高度观测的方法在能见度小于理论视距条件下也能得到具有一定精度的观测数据,具有一定的实际应用价值。

