恒等式lg2+lg5=1在解题中的作用

吴 欣

(陕西省西安市高新第二学校 713200)

例1 求值：(1) (lg5)2+lg50·lg2；

分析灵活运用恒等式Ig2+lg5=1及对数的运算法则．

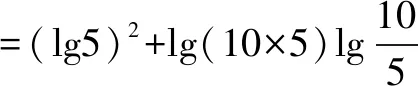
=(lg5)2+(1+lg5)(1-lg5)

=(lg5)2+1-(lg5)2=1.

方法二原式=(lg5)2+lg(52×2)lg2=(lg5)2+2lg5lg2+(lg2)2=(lg5+lg2)2=1.

(2)方法一(从左到右变形用“分”的技巧求解)

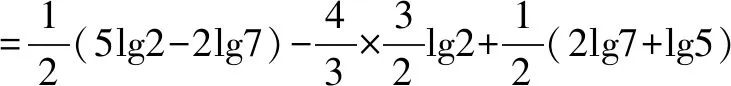
方法二(从右到左变形用“合”的技巧求解)

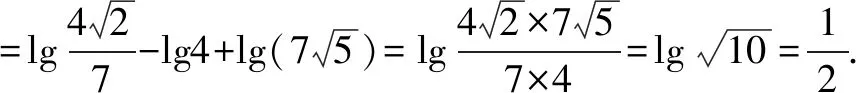
小结对数源于指数，对数与指数互为逆运算，对数的运算可根据对数的定义、对数的运算性质、对数恒等式进行．在解决对数的运算和与对数的相关问题时要注意化简过程中的等价性和对数式与指数式的互化．

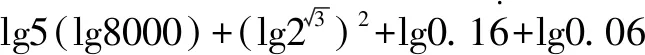
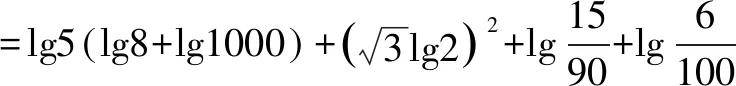
=3lg5lg2+3lg5+3lg22+0-lg6+lg6-2

=3lg2(lg5+lg2)+3lg5-2=3(lg2+lg5)-2=1.

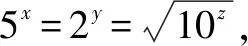
分析注意到5×2=10,lg2+lg5=1，可将所给关系式的各边取常用对数.

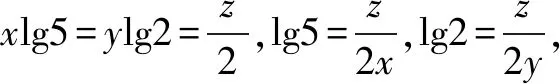
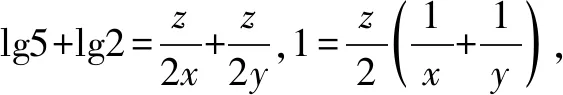
例4计算3lg2·5lg3·673lg2·5lg673.

解法一原式

=(3lg2·673lg2)·(5lg3·5lg673)=(3×673)lg2·5lg3+lg673=2019lg2·5lg(3×673)=2019lg2·5lg2019.

设m=2019lg2·5lg2019,

则lgm=lg(2019lg2·5lg2019)=lg2019lg2+lg5lg2019=lg2lg2019+lg2019lg5

=lg2019(lg2+lg5)=lg2019,

∴m=2019.

解法二3lg2·5lg3·673lg2·5lg673=2019lg2·5lg2019=2019lg2·2019lg5=2019lg2+lg5=2019.

点评解法二中，5lg2019=2019lg5，运用了恒等式alogcb=blogca，其证明如下:

设m=alogcb，则logcm=logcalogcb=logcblogca,

设n=blogca，则logcn=logcblogca=logcalogcb,

∴ logcm=logcn，m=n, 即alogcb=blogca.

如果a=c,则有alogab=blogaa=b,这就是alogaN=N形式的对数恒等式. 利用它可以简化运算.

例5计算3lg2·5lg3+673lg2·5lg673.

解法一设x=3lg2·5lg3,y=673lg2·5lg673,

则lgx=lg(3lg2·5lg3)=lg3lg2+lg5lg3

=lg2lg3+lg3lg5=lg3(lg2+lg5)=lg3,

lgy=lg(673lg2·5lg673)

=lg673lg2+lg5lg673

=lg2lg673+lg673lg5

=lg673(lg2+lg5)=lg673

∴x=3,y=673.

故3lg2·5lg3+673lg2·5lg673=x+y=3+673=676.

解法二3lg2·5lg3+673lg2·5lg673=3lg2·3lg5+673lg2·673lg5=3lg2+lg5+673lg2+lg5=3+673=676.

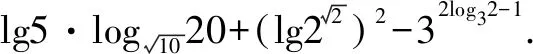
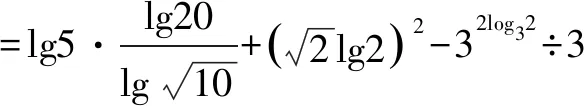
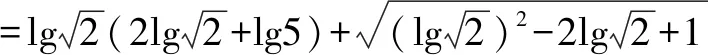
牛刀小试

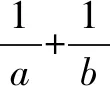
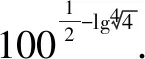
3.计算2020lg2·5lg2020.

参考答案

3.设x=2020lg2·5lg2020,则lgx=lg(2020lg2·5lg2020)=lg2020lg2+lg5lg2020=lg2lg2020+lg2020lg5=lg2020(lg2+lg5)=lg2020.

∴x=2020.

4.原式=2lg5+2lg2+lg5(2lg2+lg5)+lg22

=2(lg2+lg5)+(lg25+2lg5lg2+lg22)

=2+(lg2+lg5)2=3.