一类杆端点速度问题的多角度分析

谢汝成

(吉林省辽源市第五中学 136200)

一、提出问题：

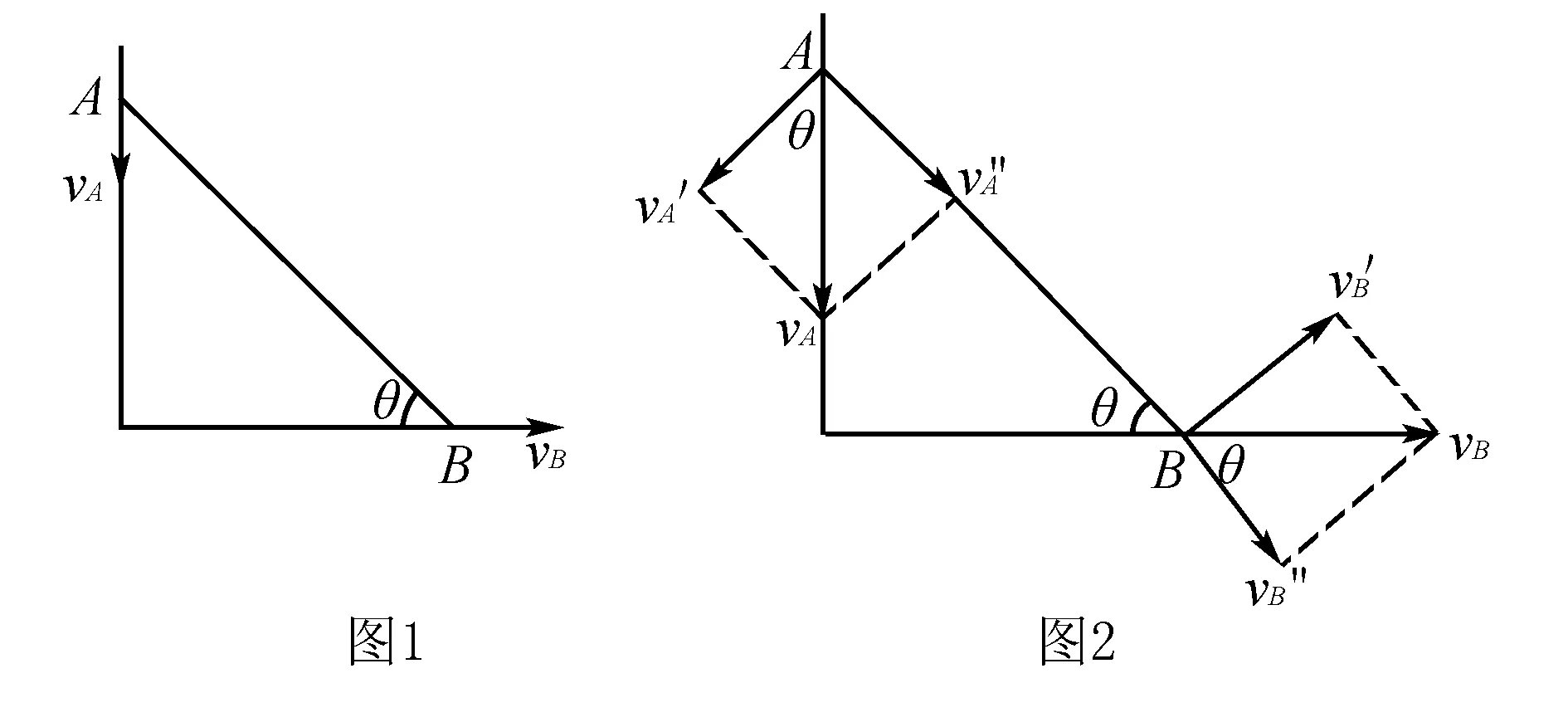
如图1所示，质量不计、长度为L的细杆，紧靠竖直墙壁放置.由于轻微扰动，杆两个端点A、B分别沿竖直墙面和水平地面滑动，当细杆与水平方向成θ角时，分析A和B两球的速度.

二、分析方法

1.绳杆约束法

不可伸长的杆或绳绕一点转动时，尽管各点速度不同，为任意两点之间的距离保始不变，故各点速度沿杆或绳方向的投影相同.

解析如图2所示，将AB两点沿墙和地面的速度vA和vB沿着杆和垂直杆分解，两端点沿杆分速度相等.

由速度矢量三角形可得

由以上三式联立可解得：vB=vAtanθ

点评此种方法为高中阶段最通用的解法，但学生没有了解到刚体和速度投影的概念，在速度分解时，学生初学时会感觉到比较棘手.常见的错误出现在将B速度分解为水平分量和竖直分量.

2.转动瞬心法

当刚体的运动既有平动又有转动时，总能找到一个瞬时速度为零的点，刚体上的每一个点都以不同的转动半径绕着该点以某一相同角速度ω转动，这一瞬时转动中心称为转动瞬心，常用C表示.若已知某瞬间刚体上两点的速度方向，且速度方向不同，可做两速度的垂线，垂线的交点即为转动瞬心.

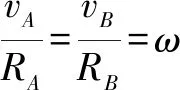
其中RA=Lcosθ，RB=Lsinθ

由上式联立可得：vB=vAtanθ

点评此种方法属于速算类解法，瞬心内容非高考考点，可作为拓展解法，拓宽学生视野，激发优等生对物理的热爱.

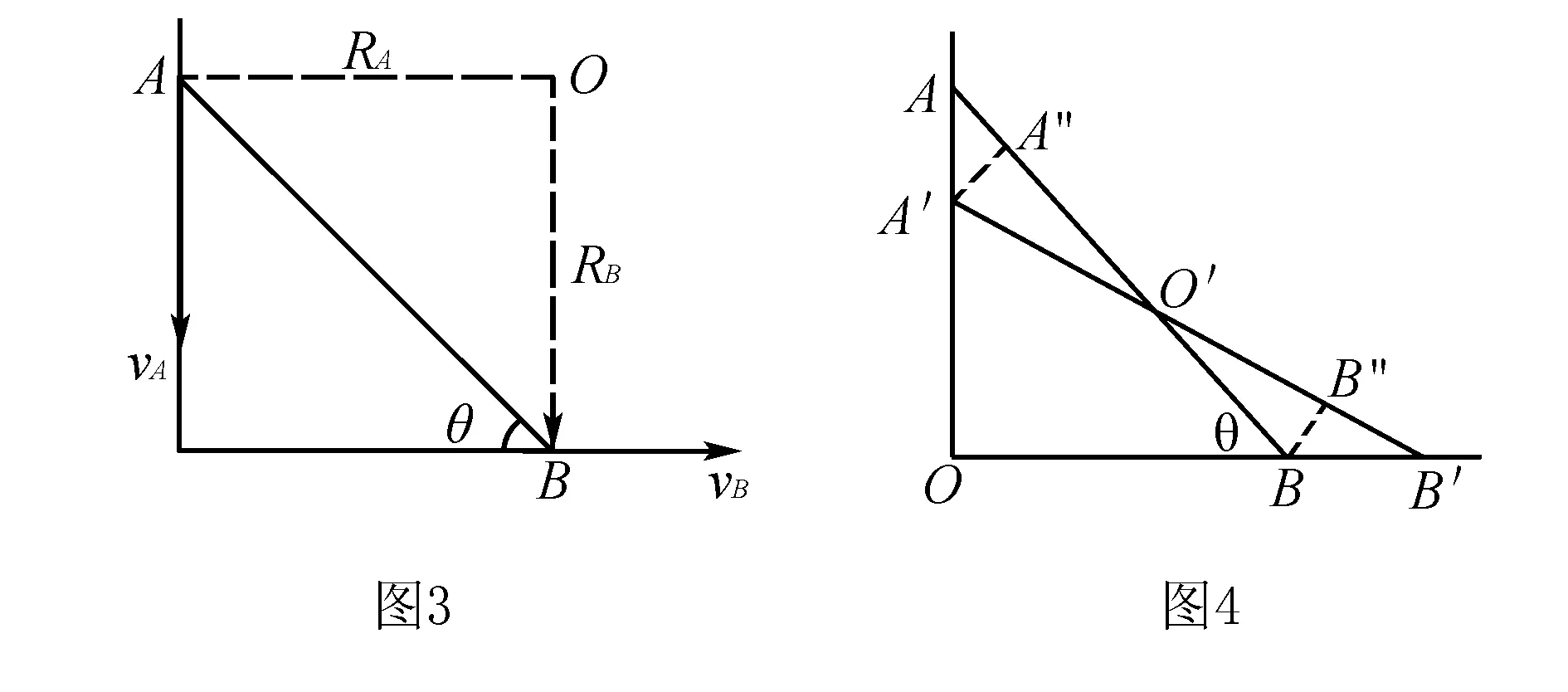
3.微元法

微元法是解决高中物理问题的常见思想方法之一，用此方法可以使一些复杂的物理问题得以简化.在使用此方法处理问题时，需要在复杂的过程中选取一段时间等物理量非常小的“元过程”，在该“元过程”中某些变化的物理量可认为不变或均匀变化，再应用相关的物理思想和数学方法处理该过程，最后通过“元过程”的分析归纳出适用全过程的结论.

解析如图4所示，设经历一小段时间Δt→0，杆AB移动到了A′B′位置，AB和A′B′交于O点，做A′A″垂直AB,BB″垂直A′B′.选取的运动时间极短，角度变化非常小可以忽略不计，速度变化非常小可近似为匀速运动.

∠A′B′B≈∠ABO=θ，∠OA′B′≈∠A′AB=90°-θ

ΔA′A″O′和ΔBB″O′为两全等三角形，A″B=A′B″

由此可得AA″=B′B″

①

其中AA″=AA′sinθ=vAΔtsinθ

②

B′B″=BB′cosθ=vBΔtcosθ

③

由①②③可得：vB=vAtanθ

点评此种方法难点在于微小量的寻找和数学关系的计算，对学生的思维要求比较高.

4.求导法

解析如图5所示，A点坐标：YA=Lsinθ

B点坐标：XB=Lcosθ

对AB坐标关于时间θ求导

表达式中的符号表示变化趋势相反，不代表大小，故在下面计算中仅带入数值大小.

vB=vAtanθ

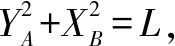
点评导数作为高等数学的基础，解决此类速度关系的优势非常明显.此种方法在物理竞赛中的应用非常广泛.

5.功率法

系统内一对内力所做的总功等于力与力方向的相对位移的乘积，若由无形变的轻质杆或绳连接着两物体，则杆或绳对两物体做的总功等于零，即杆或绳对两物体做功的功率也等于零.

解析轻杆对AB两端点的弹力方向如图6所示，杆对AB两端点的功率之和等于零.

消去F可得：vB=vAtanθ

点评：利用功能关系分析牵连速度的关系时，思路清晰，分析简单，不易出错，并且能有效的拓宽学生的视野.

6.相对运动法

知识准备：通常我们选择地面作为最大的参考系，并认为地面是绝对静止的，但当运动比较复杂时，可以选择适当的物体或点为参考系，能有效地简化分析过程.任何物体相对于地面的运动，称之为绝对运动，其相对于地面的位移和速度分别称为绝对位移和绝对速度，而相对于非地面的参考系的运动，称之为相对运动，其相对于该参考系的位移和速度分别称为相对位移和相对速度，参考系的运动，我们称之为牵连运动，其位移和速度分别称之为牵连位移和牵连速度.

绝对位移=相对位移+牵连位移；s绝=s相+s牵

绝对速度=相对速度+牵连速度；v绝=v相+v牵

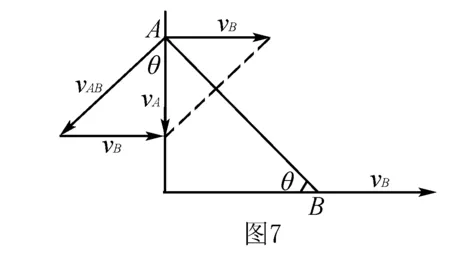
解析选择B点为参考系，则A点以B端点为圆心，以杆长为半径做圆周运动.

vA=vAB+vB

由速度矢量三角形分析可得，vB=vAtanθ

点评：在处理运动学问题时经常以地面为参考系，时间长了容易形成惯性思维，只要是运动学问题就一定选择地面为参考系.本解法旨在让学生明确，很多复杂的运动学问题，换个思路、换个参考系，就可能大大的简化问题难度，提升解题效率，本解法更有助于培养学生的思维能力.

综上所述、通过以上六个角度的分析，让学生能够比较透彻的理解牵连速度问题，同时使用多种非基础解法，有助于拓宽学生知识面.