在探究学习反思中提升数学核心素养
江苏省运河高等师范学校 (221300) 田彦军
反思是数学探究学习活动中必不可少的一个环节.反思可以是对已经学习过的知识进行归纳梳理,将现在学习的知识与已经学过的知识进行对比,达到对知识的巩固和再认识.当然也要对探究学习的过程进行反思,反思在探究活动的过程中的得与失,反思探究的结果是否正确、探究的方法是否合理、探究的过程是否科学.所以,在数学课堂教学中要注重学生反思能力的培养,不仅有利于学生进行查漏补缺,不断完善自己的知识结构,而且有利于总结自己在探究活动中的经验、方法,促进自身全面的发展.学生不仅要对自己反思,还要对他人进行反思,取长补短.实际上,在开展探究学习的过程中,不可能一下抓住数学的本质,必须要经过不断的探究和反思,才能洞察数学活动的本质特征,提高自身的数学素养.
1.对探究活动所涉及的知识进行反思
在探究学习活动中,要求学生对运用到的知识进行反思,所运用的知识是不是很清楚,是不是真正理解了,是不是能在原有的认知基础上有了更高的认识,是不是原来对知识的理解有偏差,是什么原因导致认识的偏差,在以后的学习中该注意什么.通过对知识的反思,学生不仅巩固了以前学过的知识,而且对原有知识的理解更加深刻,记忆更加清楚,丰富自己的知识结构.如果学生没有对探究学习中所涉及的知识进行反思,那么对知识的认识是肤浅的,运用知识去解决问题时就有可能出错.
案例1 如果lgx=lga+3lgb-5lgc,那么( ).
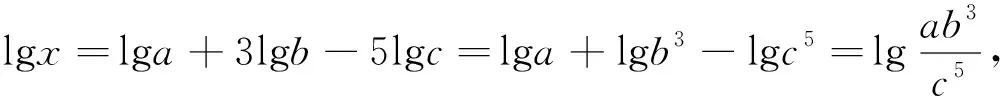
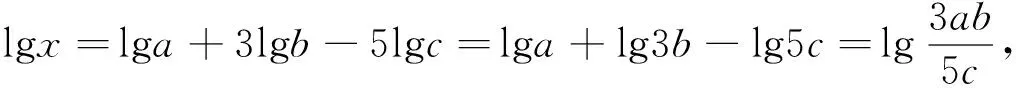
学生误解的原因是根本没有真正掌握对数的运算法则,不知道对数的运算法则是怎么来的.所以,对于对数运算法则理解不到位,和以前学习的运算法则混淆了,在运用法则去运算时出错是必然的.要避免这种现象的发生,就必须让学生真正探究对数的运算性质,并反思这种运算性质与以前学习的运算性质有哪些区别,抓住对数运算的精髓,才能掌握对数运算的实质含义.
2.对探究活动中的思维过程进行反思
在一个数学探究活动结束后,应该慢一些、停下来,让学生回味在探究的过程中的所想所做.如在进行操作时是怎么想的,为什么这样想,想了哪些问题,这些问题有研究的价值吗,在操作验证的过程中又遇到了哪些新的问题,这些问题怎么解决,这种方法为什么没有想到,是什么原因阻碍了思维的发展等等.这样的反思可以培养学生的学习能力,可以逐渐提高他们的数学素养,也是新课程标准对培养适应社会发展人才的要求.
案例2:求证:等轴双曲线上任一点到对称中心的距离是它到两焦点距离的等比中项.
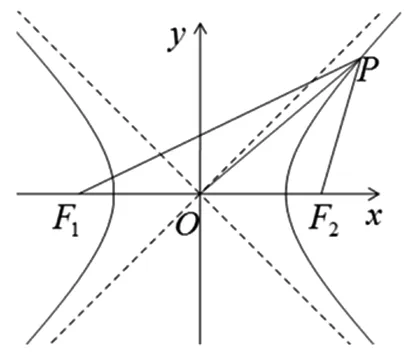
图1
只需要证明|PO|2=|PF1|·|PF2|即可.
学生经过几分钟的计算.
师:好算吗?
生:计算有点复杂.
师:你有什么好办法吗?(学生小组讨论)
生:利用双曲线的定义将|PF2|=
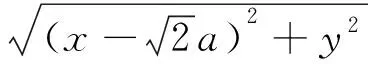
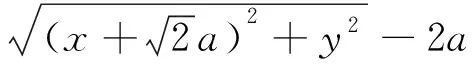
师:很好!请给这位同学掌声,这样可以简化化简的过程.
学生又经过几分钟的计算.
师:好算吗?
生:还是不太好算.
师:将|PF1|·|PF2|与|PO|2的结果进行对比, 你有什么发现?
生:|PO|2的结果没有根号,把根号去掉试试,将根号下的式子配成完全平方.
学生继续计算.
师:怎么样?配出来了吗?
生:利用等轴双曲线的方程得y2=x2-a2,将根号中的y2换掉,就可以配成完全平方了.
数学教学的过程就是对学生进行思维训练的过程,数学教学活动就是学生的思维活动,数学教学的成功就是学生思维品质的形成和思维能力的提高.在数学课堂上要尽可能让数学思维得到真实、自然的展现. 只有让学生亲自经历探究带来的困惑,才能促使学生反思推导双曲线的标准方程时如何化繁为简的,把推导双曲线的标准方程的思维迁移到这道题目上来,从而达到解决问题的目的.如果在学习《双曲线及其标准方程》这一课时,课后没有进行反思,在解决上面的问题时就会出现偏差,解题必然受阻.所以,对思维过程进行反思,是使探究学习成为有意义学习的一个非常重要的环节.
3.对探究活动中所蕴含的数学思想方法进行反思
在数学学习的过程中,蕴含了很多的数学思想方法,学生想要很好的掌握这些思想方法就要在探究学习的过程中体会、领悟、应用.如果教师直接告诉学生这里体现了什么思想方法的话,那么学生的理解不可能深刻,当遇到需要利用这种数学思想方法解决问题时,学生还会很茫然.所以,学生要在探究学习的过程中,通过不断地“反思—实践—反思”,归纳出这种数学思想方法的特点,才能更好地掌握、运用这种数学思想方法,从而提高学生分析问题、解决问题的能力.
案例3:椭圆的几何性质
(1)自主先学、小组讨论
我们从哪几个方面来研究椭圆的几何性质?怎样来研究?
生1:从范围、对称性、顶点、离心率四个方面来研究.
(2)交流展示
生2:我是从图形来研究椭圆的性质的.根据图形我们可以发现椭圆位于直线x=±a和y=±b的矩形里.
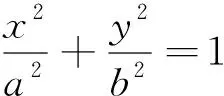
生4:将椭圆分别沿着x,y轴对折重合,说明椭圆关于x,y轴对称;将椭圆的一半拿起来绕着原点旋转180°重合,说明椭圆关于原点成中心对称.
生6:观察椭圆,可以发现有四个顶点,分别令x=0,y=0求得坐标为(±a,0),(0,±b).
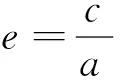
(3)质疑拓展
师:刚才几位同学说的很好.有的同学利用代数的方法来研究椭圆的性质,如生1和生3,有的同学利用几何的方法来研究几何性质,如生2和生4,还有的既利用代数的方法,又利用几何的方法,如生5和生6,这就是我们熟悉的数形结合的思想,这给以后我们研究其他的曲线的几何性质提供了方法.对这几条性质你还有要补充的吗?
生8:椭圆的离心率怎样反映了椭圆的扁平程度?
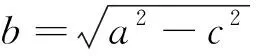
师:下面我利用几何画板来给大家演示一下.(利用多媒体辅助教学)如果a=b,则c=0,两个焦点重合,这时就是圆了.
正如华罗庚先生所言,“数缺形时少直觉,形缺数时难入微,数形结合无限好,割裂分家万事休.”数形结合,主要指的是数与形之间的一一对应关系,把抽象的数学语言、数量关系与几何直观、位置关系相互结合,使复杂问题简单化,抽象的问题具体化.研究椭圆的几何性质的过程中充分利用了数形结合的思想,使得探究出来的性质既形象又具体,由从“形”的感性认识上升到“数”的理性认识,为后续探究其他曲线性质或者解决问题提供了方法指导.
总之,在数学探究学习的过程中,学生要不断反思自己所学、所想、所做,才能深入数学内部,抓住数学的本质,掌握知识的真谛,提高思维水平,实现核心素养的真正提升.

