深挖教材习题资源 提升数学核心素养

甘肃省兰州第一中学 (730030) 岳辉平

教材是课堂教学的基本依据，是学生获得知识与方法、积累间接经验的重要途径.充分利用和挖掘教材资源，让学生获得丰富的知识与灵活的方法，体会教材的引领和示范作用，更要让学生在感知“感性——理性”这一认识规律的同时注重“理论——实践”的知识升华过程.只有这样，才能提升和发展数学抽象，逻辑推理，数学建模，数学运算，直观想象，数据分析数学学科核心素养.

函数与方程，数形结合，分类与整合，转化与化归，特殊与一般，有限与无限等基本数学思想在解决问题过程中的准确把握和合理运用正是数学素养的具体、直观体现，也是对学生从知识到能力、理论到实践学习效果的检验.

充分利用好教材资源，就是充分利用好教材严谨、准确的文字语言，简洁、规范的符号语言，直观、清晰的和图形语言和完整严、密的逻辑推理，充分利用好每一道例题、习题所体现的思路、解法及蕴含的基本数学思想，处理好问题的联系与区别、变与不变的关系、一题多解与多题一解的规律性.

解决教材的例题、习题，是学生理解和领会基本概念、巩固和掌握基础知识、获得基本技能、基本思想、基本活动经验的最基本的保障，也是规范解题格式、明确解题思路、运用数学思想检验学习效果、提高从数学角度发现和提出问题的能力、分析和解决问题能力的重要内容和环节.例题、习题的教学能更好体现教师的主导作用和学生的主体作用.然而对于教材中的例题、习题，一些教师和学生只是停留在是否完成的低层次上，错误的认为简单而忽视了对教材习题内涵和隐含的数学思想和方法的挖掘和探究，弃本求末，从而导致学生在知识、方法、思路、核心素养发展的基础不牢固而深陷题海.

笔者在一节习题课的教学中，对人教A版高中数学选修2-1第二章圆锥曲线与方程2.1曲线与方程37页练习3，让学生进行解法的挖掘和探究，激发学生的创造性思维，使学生获得了基本的活动经验.

题目如图1，已知点C的坐标是(2，2)，过点C的直线CA与x轴交于点A，过点C且与直线CA垂直的直线CB与y轴交于点B.设点M是线段AB的中点，求点M的轨迹方程.

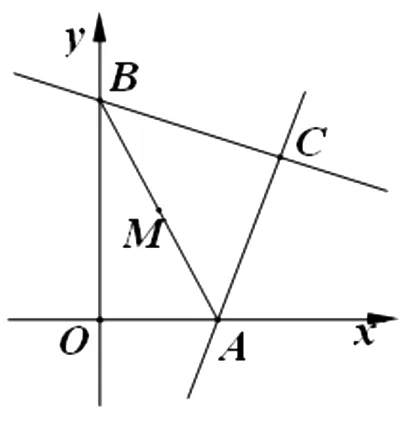
图1

为了更具有一般性,将点C的坐标是变更为(m，n)(mn≠0),以下就是课堂教学的部分情节：

提问学生并与学生一起依“求曲线方程的步骤”求得点M的轨迹方程(学生口述，教师板书)

S1:设点M(x，y)，知A(2x，0)，B(0，2y).

T:直线CA与直线CB垂直有哪些含义？

S1:直线的方向向量数量积为零；两直线的斜率互为负倒数；勾股定理.

T:你所选择的方法是？

S1:向量垂直.

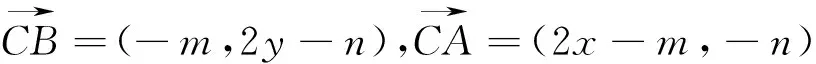
点评:逻辑推理严密,直截了当，抓住了向量数量积为零这一向量垂直的关键条件.

接着学生S2试着依斜率互为负倒数来解决，

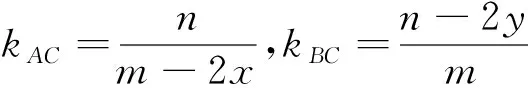
这时有学生立即补充.

综上可知:点M的轨迹方程为2mx+2ny-m2-n2=0.

教室里响起了热烈的掌声，这掌声是对S3分类讨论的充分肯定.

点评:“无法确定，立即讨论”，分类讨论思想运用熟练.

接着让学生分组讨论“垂直”条件在三角形中怎样利用.

不一会儿，大家找到了以下几种方法.

S4:根据勾股定理，由CA⊥CB知△ABC是Rt△.故∣BC∣2+∣AC∣2=∣AB∣2，得(0-m)2+(2y-n)2+(2x-m)2+(n-0)2=(2x-0)2+(0-2y)2，即点M的轨迹方程为2mx+2ny-m2-n2=0.

点评:解析法架起了“数”与“形”的桥梁，使数学运算更快.

S5:根据直角三角形斜边中点到三个顶点的距离相等，知∣MC∣=∣MA∣，得

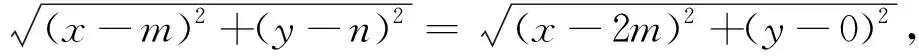
点评:熟知直角三角形性质，基础扎实，运算快捷.

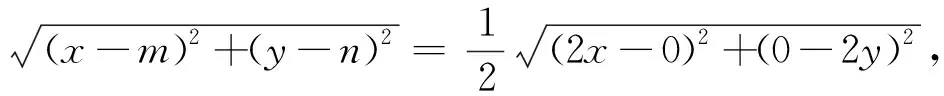
点评:线段之长转化为两点距离，转化很及时.

S7:由点M是Rt△ABC与Rt△ABO斜边的中点，知∣MO∣=∣MC∣，得

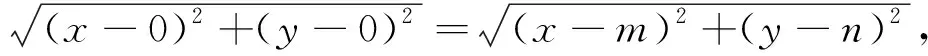
点评:直观想象到位，给大家豁然开朗的思维提示.

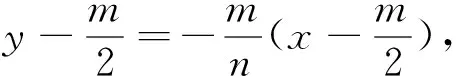
显然，S1是基本活动经验的收获者.他直接得到点M的轨迹是直线:线段OC的中垂线.

这时教室里再次响起更热烈的掌声！

评价:数学抽象及时，知识积累深厚，新思路水到渠成.

可见，让主体发挥能动作用，可以将教材资源得以充分的挖掘，对提升和发展数学核心素养非常有效.然而对这个问题的解决还没有结束，第二天本班数学科代表又呈上了如下解法:

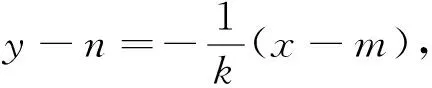
综上可知,点M的轨迹方程为2mx+2ny-m2-n2=0.

对此，我及时地给予了肯定：引入参数解决问题思路好，基础扎实，数学运算、逻辑推理、数学抽象一气呵成，值得肯定！

“数学学科核心素养的本质就是，会用数学的眼光观察世界，会用数学的思维思考世界，会用数学的语言表达世界”.一花独放不是春，百花齐放春满园.通过对教材资源深挖广拓，多角度思考，使数学学习底蕴更加深厚,根底更加牢靠，兴趣激增，探究数学知识的欲望得以极大地提高，收获满满.这无疑是提升、发展数学核心素养积极有效的途径.