一道高考解析几何题的再探究

浙江省金华市第六中学 (321000) 虞 懿

1.考题展示

(2019年高考浙江卷第21题)如图1所示，已知点F(1,0)为抛物线y2=2px(p>0)的焦点．过点F的直线交抛物线于A,B两点，点C在抛物线上，使得△ABC的重心G在x轴上，直线AC交x轴于点Q，且点Q在点F右侧．记△AFG，△CQG的面积分别为S1,S2．

图1

(Ⅰ)求p的值及抛物线的准线方程；

分析：本题以抛物线为载体，主要考查抛物线的几何性质、直线与抛物线的位置关系、重心与面积等基础知识，同时考查解析几何的基本思想方法和综合解题能力．本题设计新颖，构思巧妙，耐人寻味，令人赏心悦目，体现了“能力立意”的指导思想，凸显了数学试题的选拔功能．

由于问题(Ⅰ)较为简单，本文不作讨论，下面仅对问题(Ⅱ)进行探究．

2.解法优化

优解1：借助重心性质，实现面积比的代数表示

优解2：回归向量本质，实现面积比的代数表示

向量具有代数、几何双重身份，融数形于一体，是沟通代数和几何的桥梁．它可以将几何问题坐标化、数量化，因此它也是解决解析几何问题的重要工具．

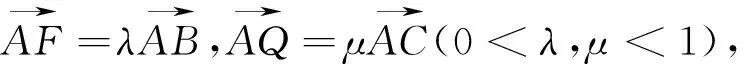
评注：在探究解题思路时，要善于从不同的角度分析、挖掘它与其他知识的联系，在平面解析几何中涉及长度、面积(比)、角度的计算及有关平行、三点共线、垂直等位置关系问题时，都可以利用向量知识加以解决．

3.多向拓广

抛物线与椭圆、双曲线“同宗同源”，那么椭圆、双曲线是否具有上述类似结论成立？回答仍是肯定的．

4.本源探究

燕尾定理：如图2所示，在ΔABC中，AD,BE,CF相交于同一点O，那么SΔAOB:SΔAOC=BD:CD．

图2

燕尾定理给出了一个转化面积比与线段比的手段，因为ΔAOB和ΔAOC合起来的图形的形状很象燕子的尾巴，所以这个定理被称为燕尾定理．该定理在许多几何题目中都有着广泛的运用，它为三角形面积比与对应底边比提供了互相联系的途径．

图3

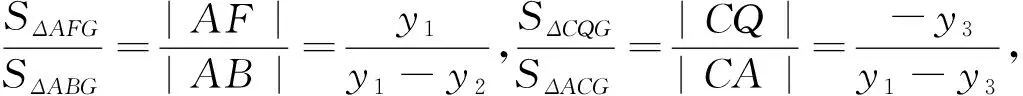
评注：可以看出，拓广4是考题的命题本质，高考试题将这个本质放在圆锥曲线中，赋予更丰富的图形与知识，进而考查直线与圆锥曲线的相关内容，考查学生的转化与化归，数形结合等思想与能力．(拓广1～3的证明，仿上述证法即可．)

事实上，解析几何问题的本质仍是几何问题，解题时要充分把握解析几何中图形的特征，紧扣其中关键的几何要素，挖掘图形相应的几何性质，恰当地运用平面几何的相关知识，将解析法与平面几何方法相结合，往往能简化运算，优化解题过程，能起到四两拨千斤的功效．

5.变式提升

变式2 如图4所示，过抛物线y2=2px(p>0)上一点P作抛物线的切线l交x轴于Q，F为焦点，以原点O为圆心的圆与直线l相切于点M．

图4

解题是一种创造性活动，作为数学的学习，积累一定的解题经验对以后解题过程中快速提取信息应该是帮助很大的，而有针对性地进行变式训练，则是解题经验自觉积累的有效途径．如在完成上面的高考问题探究后，若我们能从结论或条件的适当变化中编拟出一些问题，就可以巩固方法，辨析异同，提升能力．

对高考试题的再探究，不仅能使教师清晰地理解命题人的思想、命题背景和考查目的，还可以更好地培养学生思维品质，提高学生提出问题、分析问题和解决问题的能力，提高学生的数学核心素养．