例析函数性质的理性之美

北京市第一0一中学怀柔分校 (101407) 李加军 马 冲

我国《普通高中数学课程标准(2017年版)》明确指出:"在学习数学和应用数学的过程中,学生能发展数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等数学学科核心素养."

课程目标首先要求学生在学习数学的过程中掌握数学基础知识、基本技能、基本思想、基本活动经验(简称“四基”)；其次，在应用数学的过程中提高从数学角度发现和提出问题的能力、分析和解决问题的能力(简称“四能”)；进而在学习数学和应用数学这两个过程中发展数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等数学学科核心素养；最后，能够会用数学眼光观察世界，会用数学思维思考世界，会用数学语言表达世界(简称“三会”)．数学学科核心素养是课程目标的集中体现，“三会”是数学学科核心素养的外在表现．

函数是现代数学最基本的概念，函数性质的应用是贯穿高中数学课程的主线.本文通过对函数性质的应用,来阐述如何将数学核心素养真正落实到基础教育的主阵地——课堂教学.

一、直观发现函数性质，开门见山之美

(A)充分必要条件 (B)充分而不必要条件

(C)必要而不充分条件(D)既不充分也不必要条件

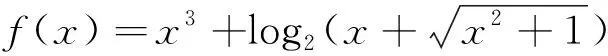
-f(b)=f(-b),有a≥-b，即a+b≥0．故选(A)．

例2 (2012全国联赛试题)设f(x)是定义在R上的奇函数，且当x≥0时，f(x)=x2，若对任意的x∈[a,a+2]，不等式f(x+a)≥2f(x)恒成立，则实数a的取值范围是.

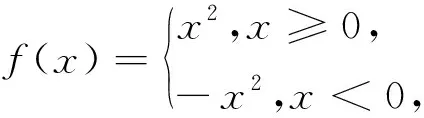
例3 (2017全国联赛试题)设f(x)是定义在R上的函数，对任意实数x有f(x+3)f(x-4)=-1，又当0≤x<7时，f(x)=log2(9-x)，则f(-100)的值为.

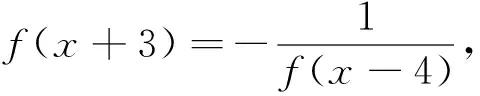
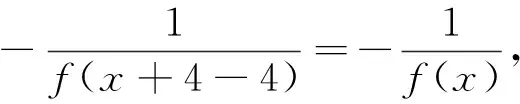
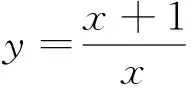
(A)0 (B)m(C)2m(D)4m

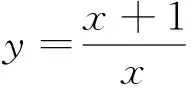
评注：课程目标要求会用数学眼光观察世界．在上述4个例子中，根据所掌握的基础知识，通过敏锐观察，发现所研究函数具有的奇偶、单调、周期、对称等性质，结合函数性质快速合理地解决问题，闪现于眼前一种开门见山之美感．

二、深刻挖掘函数性质，曲径通幽之雅

例5 (2017清华大学领军计划试题)满足(3x+y)5+x5+4x+y=0的点(x,y)( ).

(A)在一条直线上 (B)在一条抛物线上

(C)有有限个 (D)有无限个

解:由(3x+y)5+x5+4x+y=0得(3x+y)5+3x+y=-(x5+x)，令f(t)=t5+t，则f(t)在R上是增函数且为奇函数，于是由f(3x+y)=-f(x)得f(3x+y)=f(-x)，所以3x+y=-x，即4x+y=0，故答案选(A)(D)．

例6 (2015四川省预赛试题)设x+sinxcosx-1=0，2cosy-2y+π+4=0，则sin(2x-y)的值是.

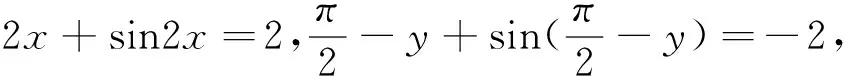
例7 (2008全国联赛试题)设f(x)是定义在R上的函数，若f(0)=2008，且对任意x∈R，满足f(x+2)-f(x)≤3·2x，f(x+6)-f(x)≥63·2x，则f(2008)=.

解:令g(x)=f(x)-2x，则g(x+2)-g(x)=f(x+2)-f(x)-2x+2+2x≤3·2x-3·2x=0，于是g(x+6)-g(x)=f(x+6)-f(x)-2x+6+2x≥63·2x-63·2x=0，所以g(x+2)≤g(x)，g(x+6)≥g(x)，故g(x)≤g(x+6)≤g(x+4)≤g(x+2)≤g(x)，所以g(x+2)=g(x)，所以g(2008)=g(0)=f(0)-1=2007，所以f(2008)=g(2008)+22008=22008+2007．

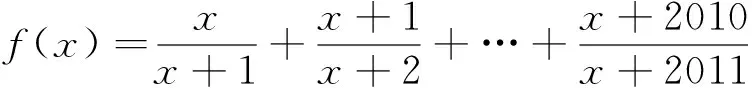
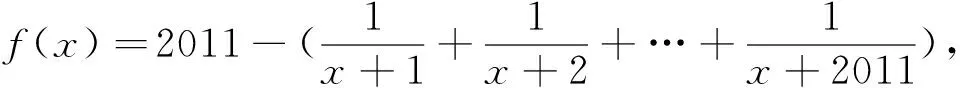
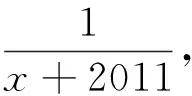
评注：课程目标要求用数学思维思考世界．上述4个例子中，通过对题目条件和结论适当变形，找到隐含的函数结构及相应的性质，然后利用函数性质对题目进行详细剖析，得到问题的结果，使人享受到曲径通幽之快乐．

三、灵活运用函数性质，豁然开朗之妙

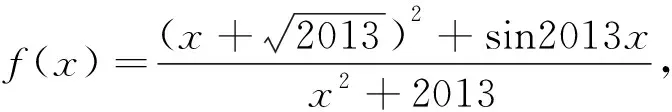
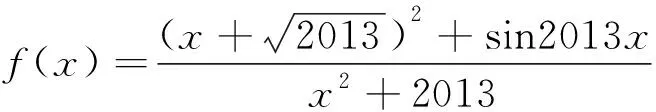
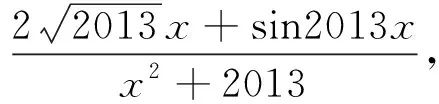
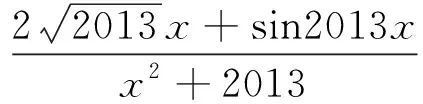
gmin(x)=0，于是fmax(x)+fmin(x)=2．

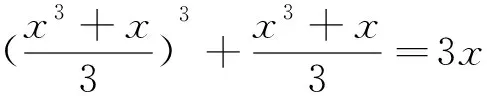
(A)0 (B)2 (C)4 (D)前三个答案都不对

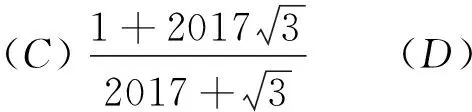
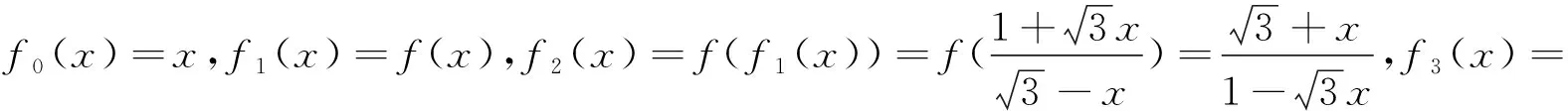
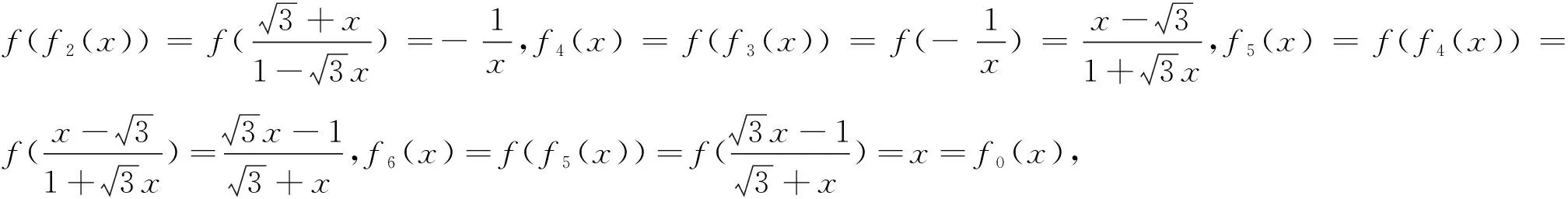
例12 (2017清华大学领军计划试题)若方程有2|x-1|+acos(x-1)=0唯一解，则( ).

(A)a的值唯一 (B)a的值不唯一

(C)a的值不存在 (D)以上答案都不对

解:令f(x)=2|x-1|+acos(x-1)，因为f(2-x)=f(x)，所以f(x)关于直线x=1对称，所以f(x)的唯一零点只可能是1，即f(1)=0，所以1+a=0，解得a=-1，此时f(x)=2|x-1|-cos(x-1)≥1-1=0，等号当且仅当x=1取到，即函数f(x)有唯一零点1，即方程有2|x-1|+acos(x-1)=0唯一解，故选(A)．

例13 (2012河南省预赛试题)若α是方程xex=2011的解，β是方程xlnx=2011的解，则αβ=.

解:令f(t)=tet，易知f(t)=tet在(0,+)上是增函数，由条件知αeα=2011且βlnβ=2011，即αeα=2011且(lnβ)elnβ=2011，所以f(α)=f(lnβ)，故α=lnβ，所以αβ=βlnβ=2011．

例14 (2018中科大自主招生试题)已知定义在(0,+∞)上的函数f(x)是单射．对任意x>0，有xf(x)>1，f(xf(x)-1)=2，则f(2)=.

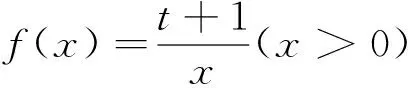
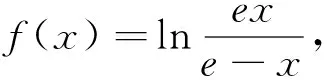
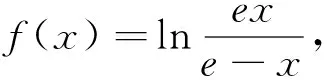
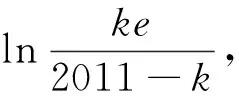
评注:课程目标要求会用数学语言表达世界．数学的应用性使得数学焕发出无穷的魅力．上述7个例子说明有意识地培养灵活的函数观念，积极解决数学自身问题，对提高一个人的数学素养有着极大的帮助．深刻认识题目中所蕴含的函数性质的本质，会让人体验到豁然开朗之愉悦．