“不等式选讲”存在问题分析及解决对策

福建省龙岩市教育科学研究院 (364000) 卢燕霞

不等式选讲为全国卷高考选考内容之一,题型较稳定，属中档题.主要考查绝对值不等式的求解、不等式证明的基本方法(比较法、综合法、分析法等)及根据给定条件求参数的取值范围、用基本不等式研究代数式的最值及证明不等式等问题，交汇考查集合的概念、绝对值的概念、函数的概念、函数的图像与性质、二次不等式、基本不等式等内容.试题分两问，第一问多为考查解绝对值不等式或利用基本不等式求最值；第二问多为考查不等式恒成立问题或根据给定条件求参数的取值范围或利用基本不等式证明不等式.考查运算求解能力、推理论证能力，考查的核心素养是逻辑推理、数学运算.下面我将对学生在此专题学习过程中存在的主要问题进行剖析，并提出相应的解决问题对策.

一、存在的问题及原因分析

1．绝对值不等式求解技能掌握不到位

解绝对值不等式的关键是去绝对值符号，等价转化为不含绝对值符号的不等式，然后用已有方法求解.但面对具体问题的多样形式有不同的求解方法与技巧，如平方法、零点分段讨论法、利用绝对值的几何意义等，不少同学对此掌握不到位.

例1 (2017全国Ⅰ卷23(1))已知函数f(x)=-x2+ax+4，g(x)=|x+1|+|x-1|．当a=1时，求不等式f(x)≥g(x)的解集.

解析:当a=1时，f(x)≥g(x)等价于-x2+x+4≥|x+1|+|x-1|①.

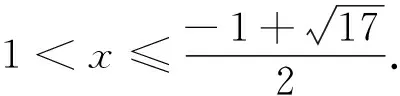
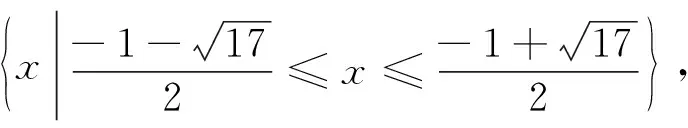
2．不能对条件进行正确的等价转化

等价转化思想是一种重要的数学思想，在解题中的作用往往体现为化复杂为简单、化陌生为熟悉，但在考试中不少同学对不等式的有关条件不能进行正确转化而导致失误.

例2 (2017全国Ⅲ卷23(2))已知函数f(x)=|x+1|-|x-2|.若不等式f(x)≥x2-x+m的解集非空，求m的取值范围.

解析:原式等价于存在x∈R，使f(x)-x2+x≥m成立，即[f(x)-x2+x]max≥m.

设g(x)=f(x)-x2+x，由已知得

当x≤-1时，g(x)=-x2+x-3

评析:本题主要考查不等式解集的概念、绝对值的意义、二次函数区间上最值等基础知识.解答中的主要问题还是在题意的理解与问题的等价转化.错点一，将“不等式f(x)≥x2-x+m的解集非空”等价转化为f(x)max≥x2-x+m解集非空，忽略了右边的代数式也是随着x的变化而变化，左右两边的x表示的是同一个数；错点二，将“不等式f(x)≥x2-x+m的解集非空”等价转化为“m≤g(x)min”，错在对“解集非空”的理解上.所谓“解集非空”即存在x使得不等式f(x)≥x2-x+m成立，等价于存在x使得不等式|x+1|-|x-2|-x2+x≥m成立，等价于(|x+1|-|x-2|-x2+x)max≥m即可.

3.不等式证明思路不清，无法迅速找到切合题意的证明方法

不等式的证明首先需要把握思路，没有明确的证题思路就会陷于混乱之中，导致简单问题复杂化，或者证明过程不完善.

例3 (2019全国Ⅰ卷23)已知a,b,c为正数，且满足abc=1，证明：

(2)(a+b)3+(b+c)3+(c+a)3≥24.

(2)由基本不等式且a,b都是正数得a+b≥

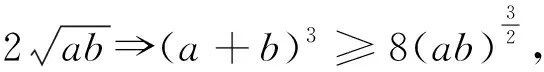
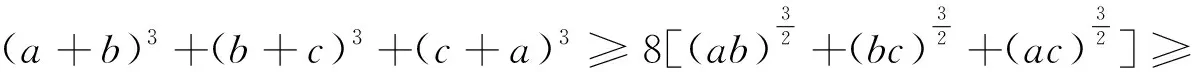
评析:本题主要考查基本不等式、不等式的证明方法等基础知识，难点在于寻找突破口，不懂利用已知条件abc=1，合理转化为待证不等式，导致无从下手；另外，解题思路不清晰，盲目解答，目标导向意识与解题策略选择意识不强，不能依据题意合理选择不等式的证明方法.

4.知识掌握不到位，无法优选算法化简求解过程

不少不等式问题的求解与求证可有不同的角度，即不同的方法，这时不同方法的选择就会对求解(证)过程的繁简产生影响，而是否能优选算法依赖于对知识与方法的到位与熟练的把握，依赖于平时对相关问题的反思与感悟.

解析:(法一)因为a>0，所以

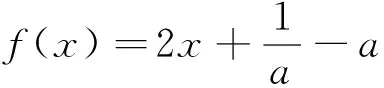
综上,得f(x)≥2成立.

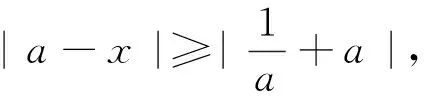
评析:法二根据绝对值不等式的性质直接证得结论，相比法一快捷明了.本题的主要问题在于对绝对值不等式的性质掌握不到位，导致无法快速求解.

二、解决问题的对策

1．强化绝对值不等式的求解训练

绝对值不等式的求解问题是高考全国卷常考知识点，可以归纳为写成分段函数求解、利用函数图象求解、利用绝对值不等式性质求解等方法.应全面加强基本概念、基本方法、基本技能的学习，熟练掌握解绝对值不等式问题的常规题型，重视不等式证明的通性通法，做到既能正确分类，又能合理整合，准确快捷解答，同时注意对求解过程等价性的关注.

2．加强对不等式“恒成立”、“能成立”、“恰成立”等几种模型的识别及求解能力

不等式“恒成立”、“能成立”、“恰成立”是高考的常见模型，解决问题的关键是对其进行恰当的等价转换，并借助函数与方程思想，数形结合思想，利用函数图象、函数最值等来解决问题.复习过程中可通过一题多变强化对上述各种模型的识别，掌握其解决方案.

3．关注基本不等式、绝对值不等式性质的应用

基本不等式、绝对值不等式性质在求最值、证明不等式等方面都有很重要的作用.应用基本不等式或绝对值不等式性质求最值时，均应注意等号成立的条件是否具备，当且仅当等号成立的条件具备时方可应用其求最值，这也是用基本不等式或绝对值不等式性质求最值的一个易错点，应引起关注.

4．加强审题能力的训练，培养审题意识

应加强审题能力的训练，培养审题意识，锻炼审题耐心.备考中可适当总结一些典型题型，归纳解题的思想方法，学会具体问题具体分析的解题意识，对于有多种解法的情形，应学会选择最有效的方法.