例析解几中涉及三角形面积的多种题型
江苏省苏州市吴中区苏苑中学 (215128) 蒋 艳 杨品方
在高中的数学解题中,有关三角形面积的题目尤其多,本文拟看看与解析几何中曲线有关的三角形的面积问题.这类问题,除了能考查三角形面积的计算,还能考查曲线的性质,还能考查用代数运算来研究几何图形的思想,所以备受数学爱好者的青睐.本文略举几例来说说该类三角形面积问题的常用处理方法,供探讨.
题型1转化面积的比值为线段长度的比值
初中学习过“相似三角形”,有个知识点叫“面积比是相似比的平方”.由此可见,处理两个三角形面积比值问题,不一定要计算面积,合理转化就可以了,可以转化到弦长.

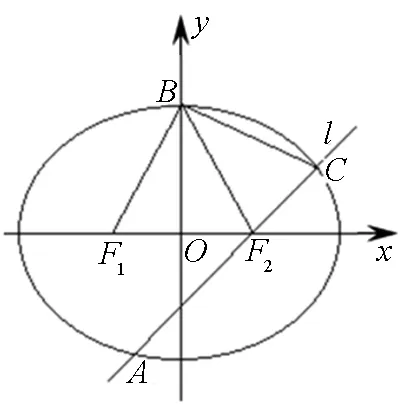
图1
(1)求椭圆的方程;
(2)过右焦点F2的直线l与椭圆交于A,C两点,记ΔABF2,ΔBCF2的面积分别为S1,S2,若S1=2S2,求直线l的斜率.
分析:题中涉及的两个三角形,如果分别选择AF2,F2C作为底边,那么它们的高是一致的,所以面积比就可以转化为底边的比值,不需要具体求面积.
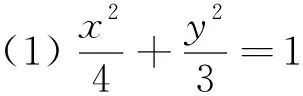
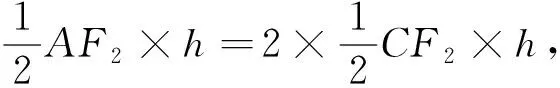
点评:如果费尽辛苦先求得点B到直线AC的距离d作为三角形的高,计算时候还是要约分约掉的,没有必要计算.
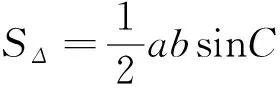
《解三角形》章节学到过已知“两边一夹角”求三角形面积的公式,在解几运算中用起来也相当方便.
例2 如图2,已知圆C:(x-a)2+(y-a)2=1(a>0)与直线y=3x相交于P,Q两点,则当ΔCPQ的面积最大时,实数a的值为.
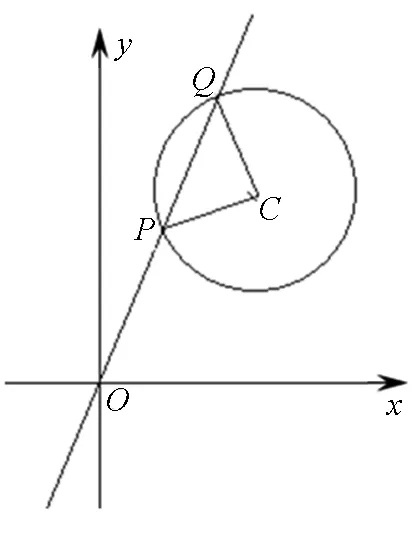
图2
分析:等腰ΔCPQ的腰长是定值1,面积就仅仅受顶角所限制,写出面积与顶角的关系式来寻求最大值.


题型3运用割补法转化再求面积
初中学过,不规则图形的面积,可以采用割补法来进行求解,我们发现,在坐标系中的三角形,由于坐标轴的特殊位置,可以恰当分割来简化运算.
图3
(1)求椭圆C的方程;
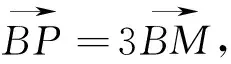
分析:M是线段BP的三等分点,可以求得M的坐标.
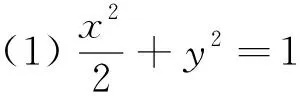
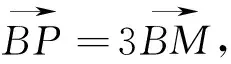
(1)模拟酒配方。调整蔗糖含量为20 g/L,不添加乙醇和磷酸氢二铵,其余成分同1.3.1中扩培阶段模拟酒。
点评:不难发现,当三角形的一条边在坐标轴上时,面积计算相对简单点,可以把坐标轴上的边作为底边,另外一个点的横(纵)坐标的绝对值就是三角形的高了.
补形与分割是相对的,鉴于“有边在坐标轴上的三角形容易算面积”,我们可以把被坐标轴分割的三角形分割成两个小三角形.
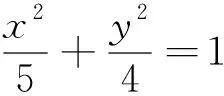
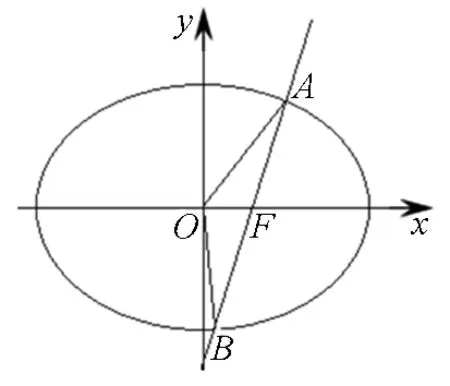
图4
分析:ΔOAB被x轴分成上下两块ΔOFA和ΔOFB,而这两个三角形,又是有边在坐标轴上的,方便计算面积.
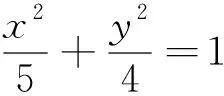
点评:在具体运算过程中,应培养敏锐的观察能力,本题中右焦点(1,0),下顶点(0,-2),两点的连线的斜率,就是已知条件中的2.同样是消元,消去y得到x的方程,应该更容易计算.
题型4运用公式“底乘以高再除以2”
对于一般三角形,如果可以直接获得底和高,那么我们就采用“底乘以高再除以2”来计算面积.
例5 如图5,已知抛物线C:y2=4x的焦点为F,点D为其准线与x轴的交点,过点F的直线l与抛物线相交于A,B两点,求ΔDAB的面积S的取值范围.
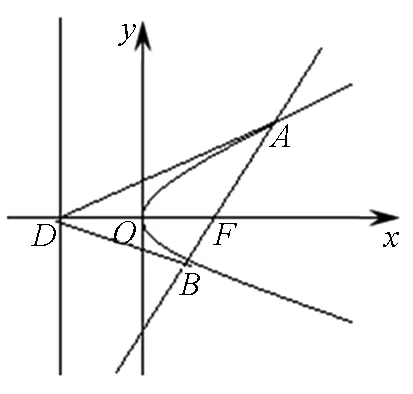
图5
分析:通过联立方程,可以得到弦长AB,还可以得到点D到直线AB的距离,于是就有ΔDAB的面积了.
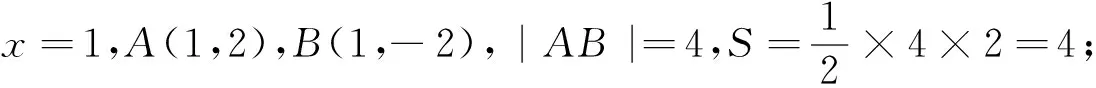
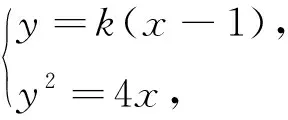
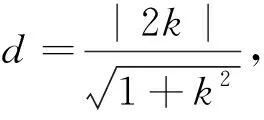
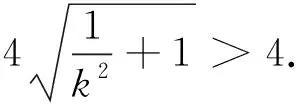
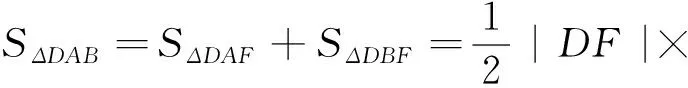
|y1-y2|,这时候需要把直线AB的方程写成x=my+1再联立方程,而计算|y1-y2|则是弦长AB的一小步,区别不大.
解析几何中,涉及曲线的三角形的面积的计算,有时候不需要面积公式,可以转化到线段长的计算;更多时候需要我们合理分析,选择“两边一夹角”呢还是“底乘以高再除以2”呢,还是先进行必要的分割再行计算,需要我们分析与观察并举.

