多角度解决典型问题，提升物理学科核心素养

◇ 山东 陈 强

物理学科核心素养是学生在接受物理教育过程中逐步形成的适应个人终身发展和社会发展需要的必备品格和关键能力，是学生通过物理学习内化的带有物理学科特性的品质，是学生核心素养的关键成分.物理课堂有不同的类型，不同课型需通过学习体验积淀的学科素养也不尽相同.长期实践表明：在习题课中积极引导学生多角度、多方位思考问题，采取构建物理模型、一题多解、多解归一的方式，对于培养学生的科学思维和实验探究的物理学科核心素养有着不可替代的作用.下面笔者根据板块模型中一道典型例题的多种解法加以说明.

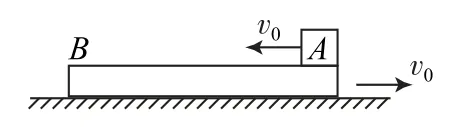
图1

解法1动力学法

分别选取A、B 为研究对象进行受力分析，根据牛顿第二定律对小物体A 有Ff＝maA，对木板B 有Ff＝MaB.因为m＜M，所以aA＞aB，且A 刚好没有滑离B 板，所以木板B 向右做匀减速运动，小物体A先向左做匀减速运动至速度为零，再向右做匀加速运动，最终经时间t 与B 共速.规定水平向右为正方向，设二者共同速度为vB，对小物体A 有

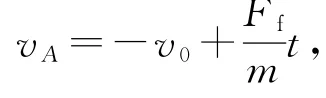
对木板B 有

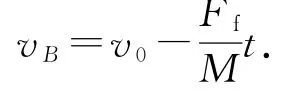
联立以上两式，解得

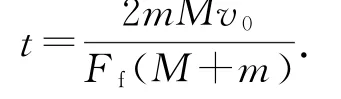
此过程小物体A 向左运动的距离为

木板B 向右运动的距离为

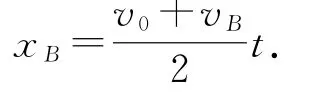
因此小物体A 最终相对于木板B 静止时与木板B 右端的距离

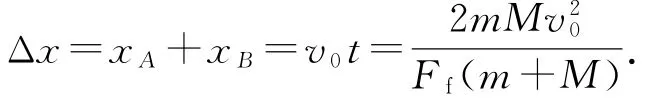
解法1(动力学方法)是处理物理问题的基本方法，也是学生最容易想到的方法.但对于此题，由于小物体A 运动(先向左匀做减速直线运动，再向右做匀加速直线运动)的复杂性，加之学生对矢量运算掌握不到位，笔者发现只有部分同学能够完整利用此方法完成这道题.因此在给出解法1后笔者又引导学生作进一步思考：能否避开繁杂的中间过程，利用整体法处理该问题.很快，学生给出了以下两种比较典型的解法.

解法2功能关系法

因为小物体A 和木板B 组成的系统不受外力，所以系统动量守恒，设二者最终达到的共同速度为vB，规定水平向右为正方向，根据动量守恒定律有

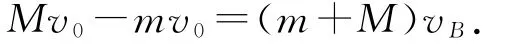
再对小物体A 应用动能定理有

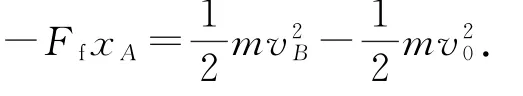
同理对木板B 用动能定理有

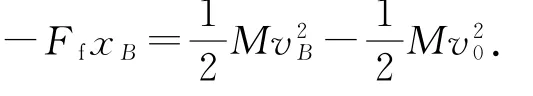
联立以上各式，可得小物体A 最终相对于木板B静止时与木板B 右端的距离

解法3图象法

规定水平向右为正方向，分别作出木板和小物体A 运动的v-t 图象，如图2所示，由图象可知，阴影部分的面积大小即为二者的相对位移，即

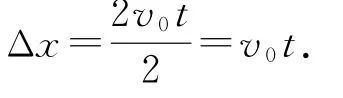
根据动量守恒定律有

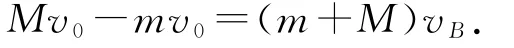
对木板B 由动量定理有

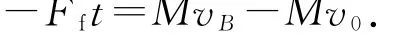
联立各式，解得

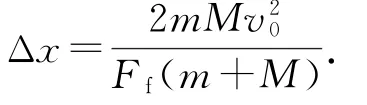
图2

可以看出，同一物理过程，应用不同的物理规律，解题过程繁简程度不同，思维过程也不同.在解法2中，将A 的两个小过程整体考虑利用动量和能量观点求解，使得解题过程和思维过程大大简化.通过解法1、2的对比，可以帮助学生建立对于多过程、多对象问题，若不考查中间过程，优先考虑动量和能量观点处理的科学思维.解法3数形结合，将抽象的物理过程形象化，也是物理中常用的解题思路.通过对比解法3与1、2，可以看出图象法对于解答多过程物理题目具有一定的优越性，但图象的绘制是教学难点.

上述三种解法是我们解决物理问题常用的方法，思维清晰严谨.其实对于基础较好的学生，还可以引导他们利用相对运动将两个物体的运动转化成一个物体的运动，得到解法4.

解法4相对运动法

以木板B 为参考系研究物体A，取向左为正方向，则物体A 初速度为vA0＝2v0，加速度为

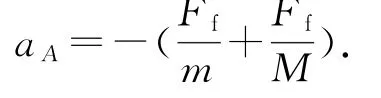
物体A 相对于木板B 向左做匀减速直线运动，直到末速度减为零，根据0－＝2aAxA，解得

笔者认为解法4虽然思维起点比较高，但更加巧妙而且富有物理韵味，不仅体现物理的思想，更能让学生深刻理解动力学方法中涉及的变速直线运动公式、牛顿第二定律的深刻内涵，而且学生也能从不同的解题思路和方法中体验学习的乐趣.总之，我们在教学中要针对一些典型问题故意设置一些情境，引导学生多角度、多方位思考，这是提升学生物理学科核心素养的有效途径.