“神来之笔”何处觅———基于两类多元最值问题“配凑法”的探究

◇ 山东 俎德鹏

纵观高中数学各个模块的内容，求最值是高中数学的重要内容，涉及的知识点广，尤其与不等式知识的结合问题，其难度更是直线上升.在各地模拟考试试题及高考真题中，不乏有经典题型出现，常以压轴题为主，其解答不仅精彩绝伦，而且在关键“配凑”处理上，更是“神来之笔”.本文就对两类多元最值求解中的关键配凑法展开研究，希望能以点破面，对读者有所启发.

1 “极值型”配凑

问题分析“双变量最值”问题，策略——消元，特点——齐次.

尝试解答

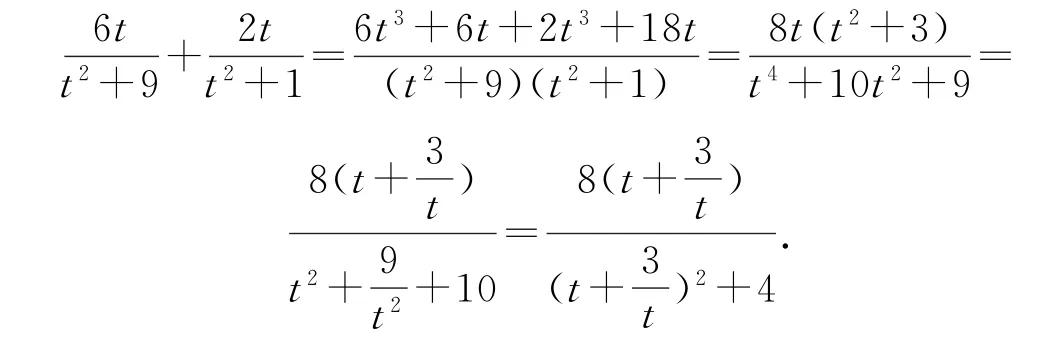
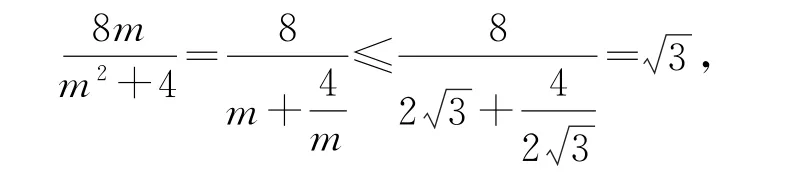
疑问二次换元是否偶然，即t＝3是否另有深意，命题者命制该题的背景又是什么?

再解答疑问的解答，笔者认为应从消元说起，对于齐次，其实有诸多消元方法.

解法1

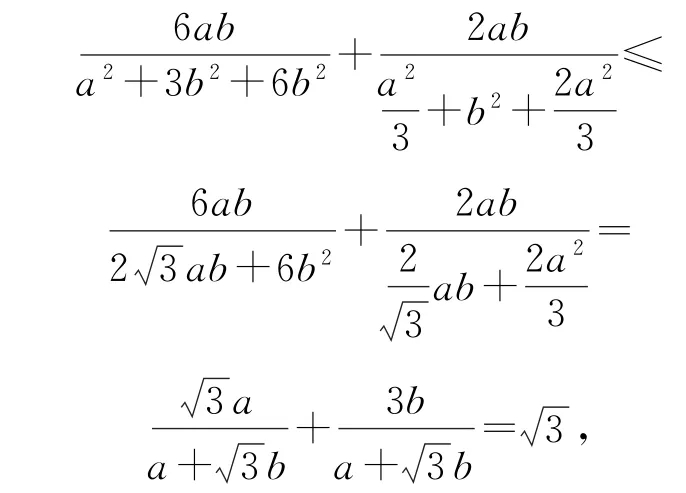
解法2

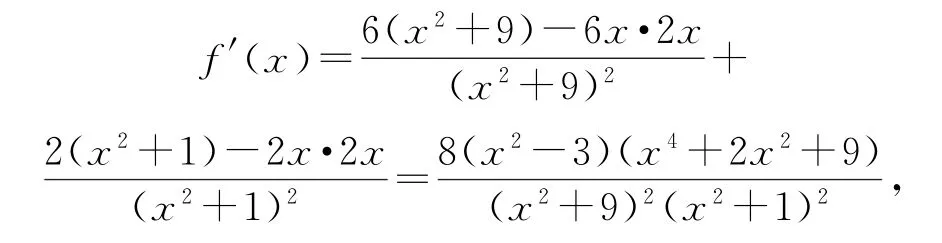
乍一看解法1 的“配凑”和解法2 公因式“x2－3”的提取如神来之笔，令人叹为观止，但仔细分析会发现其本质无非是函数极值点的巧妙应用罢了.因此函数“极值型”多变量最值问题，寻找极值点是关键，诸多的换元手法无非是让函数便于研究，让极值点显化罢了!

2 “等地位”轮换配凑

问题分析“三元最值”问题，直接消元一般难以下手，三元到二元的转变势必还需要一个等式.但已知平方和为定值，求解的整式为变量积之和，可考虑“配凑”待定系数法，用均值不等式求解，再关注已知条件和求解结论的对称式特性，就不难想到a，c 的“地位”等价性了.

尝试解答

不妨设x，y，z＜1，则

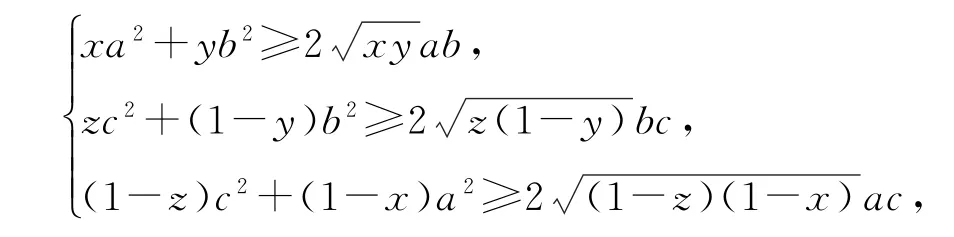
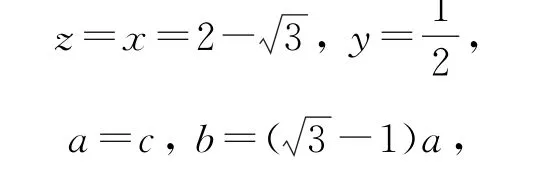
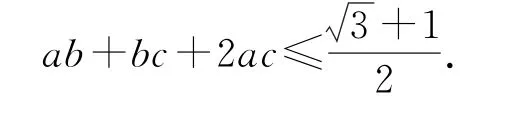
疑问上述求解较为烦琐，在配凑系数时能否有依据可循? 依据又是什么?

再解答笔者试着用拉格朗日数乘法，解释系数配凑的内在联系.

令

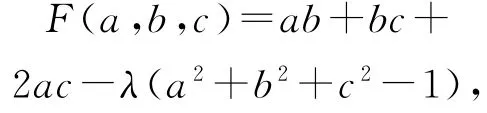
则

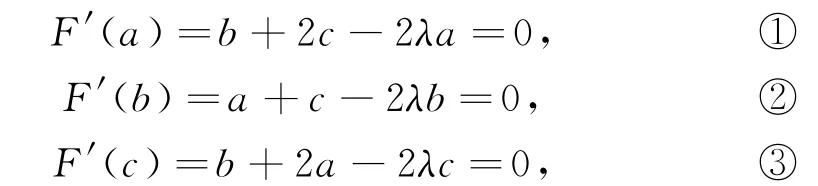
由①③得a＝c，代入②得

至此，解答可以优化，对系数的待定可以做到有的放矢.

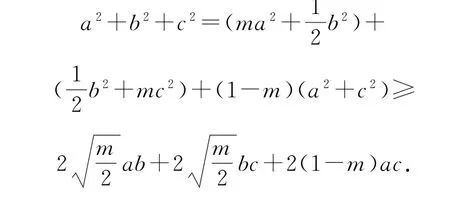
将b2拆分成并非偶然，除了从拉格朗日数乘法的角度分析配比系数之间的关系外，我们也可以从式子的结构加以分析，条件a2＋b2＋c2＝1，结论ab＋bc＋2ac，已知和求解中的等式皆是关于变量a，c轮换对称，a，c 的地位一致，故而均分b2，至此，这类问题配凑也迎刃而解.

变式已知x，y，z＞0，求的最小值.

因为x，y“地位”的一致性，可轮换，故而可均分z2，解答如下.

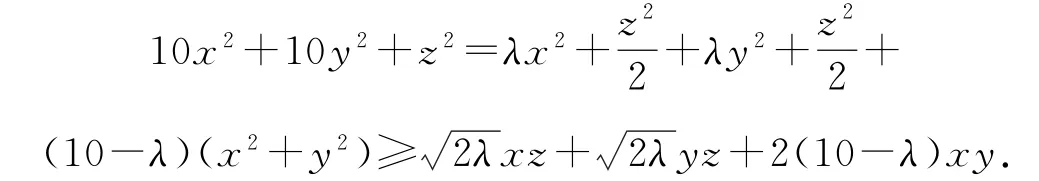
笔者认为数学学科核心素养中，逻辑推理能力是非常重要的一种能力，作为一线教师的我们，在繁忙的教学工作中，时常忽略了标准答案中解法所蕴含的“深层逻辑”，尤其是不等式配凑问题中，往往被其“神来之笔”的配凑所惊艳，继而感叹了之，而不对其内在逻辑进行深入思考.若是对其深究，我们往往可以发现问题的本源，以法破类，继而促进我们的教学工作，以达到学而思、思而悟的目的.