构建几何模型,突破平面向量难点问题
◇ 福建 林良斌
高中的向量问题兼具了数与形的两个特征,数是通过代数运算求解,形则更需几何观察.本文将从形的角度出发,通过构建几何模型,实现多思少算,提高向量问题的解题效率.
1 构造向量减法的三角形模型
从同一点出发的两个向量a,b,它们的差a-b是向量b 的终点指向向量a 的终点的向量,通过向量减法的几何意义,我们可以把一些相关问题转化为三角形问题来解决,使代数问题几何化,解题更加直观和简单.

如图1所示构造三角形,由于(a-b)⊥b,则该三角形为直角三角形,又因|a|=2|b|,所以a 与b 的夹角为.
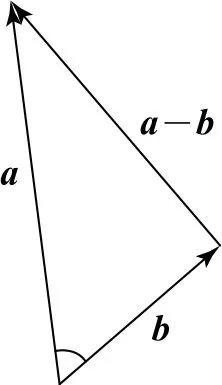
图1

对比代数方法的解答过程,通过构建向量减法的几何模型,只需作图观察,问题的解决变得一目了然,省去了代数计算的烦琐.

如图2 所示,对任意的实数λ,当|a-λb|取到最小值时,(a-λb)⊥λb,此时,|a|=2,|a-λb|=,所以|λb|=1.又因为|b|=1,所以λ=±1.
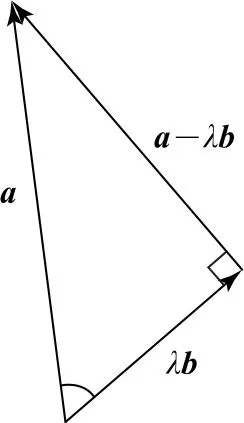
图2

在减法模型的基础上加上变量λ,使向量aλb 的起点在向量b 所在直线上滑动,形成一个动态模型,由于垂线段的长度最短,所以能轻易破解题目的难点,减少了构造函数求最值的过程.
2 构造圆的模型
圆的定义就是到定点距离等于定长的所有点的集合,若一个向量a 的模|a|为定值,并且固定其起点,那么终点的轨迹就是一个圆.


图3

在减法模型的基础上,这里向量差的模是一个定值,如图3,向量m 的终点轨迹构成了一个圆,利用圆上的动点到圆外一点的距离最大值结论来解决问题.
3 构造平行四边形对角线模型
向量的加减运算包含很多平面图形的性质,把向量a,b 的和与差求平方和,会得到这两个向量模的平方和的2倍,即|a+b|2+|a-b|2=2|a|2+2|b|2,利用这一性质可以把问题几何化,使问题更加直观.

由于|a+b|2=|a|2+|b|2+2a·b;|a-b|2=|a|2+|b|2-2a·b,所以|a+b|2+|a-b|2=2|a|2+2|b|2=10.
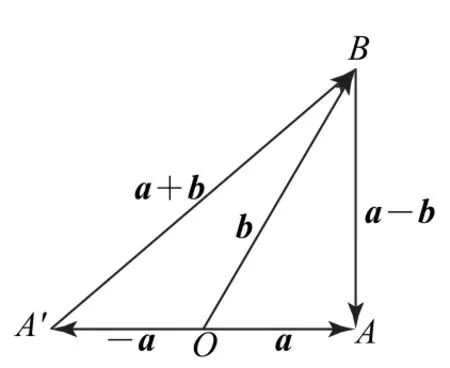
图4
令x=|a+b|,y=|a-b|,所以x2+y2=10(x,y≥1),其图象为一段圆弧MN,如图5所示,令z=x +y,则y=-x+z,所以当直线y=-x+z 过M,N两点时,z 取最小值是4.当直线y=-x+z 与圆弧MN 相 切时,z 最大.
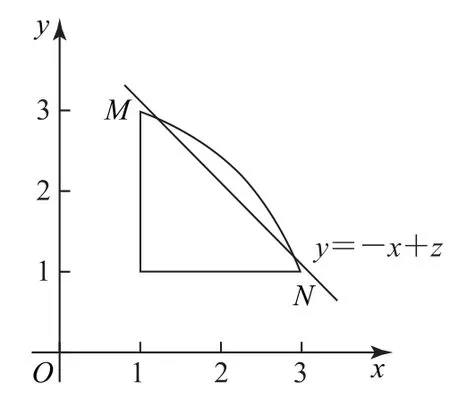
图5

平行四边形的对角线的平方和等于四条边的平方和,这个几何模型的运用将原来的问题转化成了线性规划问题来解决,更为简便.
4 构建向量数量积的几何模型
两个向量a,b 的数量积a·b=|a|·|b|cos〈a,b〉,其中|b|cos〈a,b〉就是向量b 在向量a 方向上的投影,利用这个模型可以将一些复杂的问题简单化.

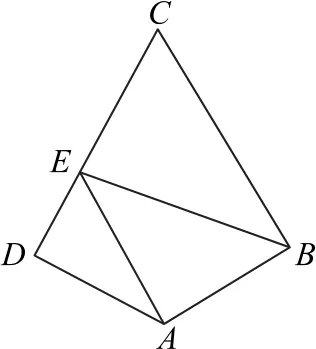
图6

所以
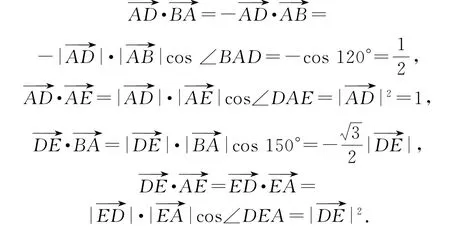

利用向量数量积的几何模型,特别是在直角三角形中,如图7,直角△ABC中有成立,通过这样的模型转化,把复杂的数量积运算过程变得很简单.
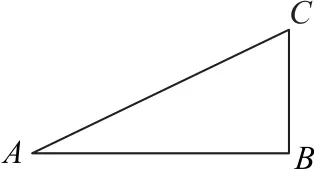
图7

如图9所示,延长AO交圆O 于点D,连接BD,CD,所 以 ∠ABD =∠ACD=90°.

图8
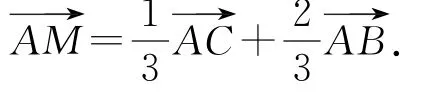
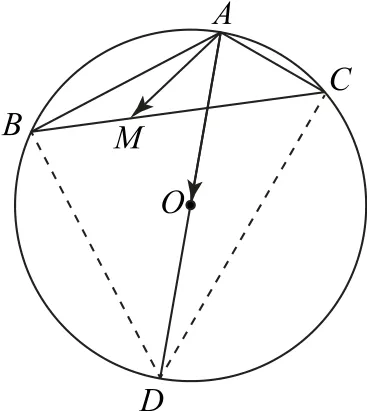
图9
所以
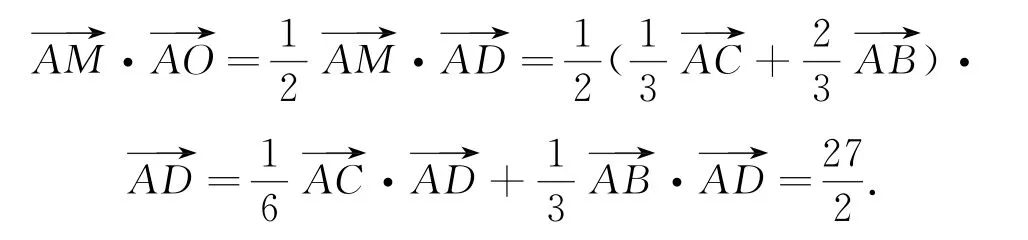

本题如果从代数角度考虑将难以入手,这里考虑几何模型,延长半径构造出以圆的直径为斜边的两个直角三角形,从而构造出数量积的几何模型.
综上所述,向量的综合题往往难度比较大,学生往往习惯用代数方法和几何方法进行求解.代数法,由于计算复杂,很多学生都陷入无休止的计算中.掌握几种常见的向量几何模型,既能有效帮助学生掌握几种基本的方法,摆脱烦琐的计算,又能使他们在这几种模型的处理方法上举一反三、触类旁通,在解决问题时有另一种思路或者选择.

