相对运动在天体运动中的应用

◇ 山东 杨清梅

运动的相对性首先体现在参考系的选取上，合理选取参考系，有时可使复杂问题得以简化，从而优化解题过程.在直线运动中，矢量方向单一，相对速度、相对加速度、相对位移易于求解，学生能很好地运用相对运动思想分析问题；而在曲线运动中，学生相对运动的意识较为淡薄，如天体运动中的共线次数和通信联络问题，由于涉及两个物体的转动，加之圆周运动的周期性，多数学生会在寻找运动位置和构建运动情境的过程中迷失方向.其实，对于这一问题，倘若能够选择合适的参考系，进而从相对运动的角度进行分析，问题便可顺利解决.

1 圆周运动中的相对运动基础

如图1所示，质点a、b 绕O 点做同向匀速圆周运动，t＝0时，二者均在Ob 连线上，它们做圆周运动的角速度、周期、t时间内转过的角度分别为ω1、ω2，T1、T2，θ1、θ2；假 设ω1＞ω2，质点a 相对质点b 的角速度、相对周期、相对转过的角度分别为ω′＝ω1－ω2，T′＝T2－T1，θ′＝θ1－θ2，相互关系为ω′＝.

图1

2 相对运动在天体运动中的应用

2.1 天体运动中的共线次数问题

A.a、b 运动的角速度之比为ωa∶ωb＝8∶1

B.a、b 运 动 的 周 期 之比为Ta∶Tb＝8∶1

C.从图示位置开始在b 转动1周的过程中，a、b、c 共线12次

D.从图示位置开始，在b 转动1周的过程中，a、b、c 共线14次

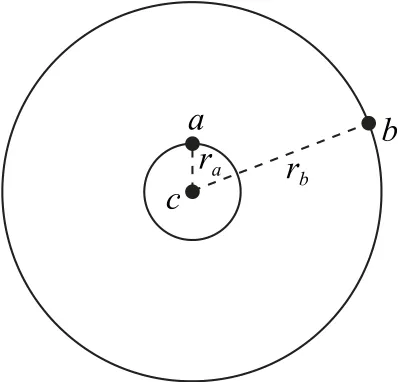
图2

2.2 天体运动中的通信联络问题

图3

在上述2个例题中，通过参考系的转换，将多个物体的转动问题，转化为单个物体的转动问题，从而使运动过程和问题情境变得简捷而清晰.所以，相对运动作为研究运动学乃至整个物理学的基础，在很多情况下，合理选择参考系，能很大程度上减少运算量，简化解题步骤，提高解题速度.