例析高中数学函数解题思路的多元化

◇ 山东 伊淑桥

1 直接观察法（定义域法）

例1求解函数的定义域及值域.

解析

由此推出函数的值域为［3，+∞）.

点评

针对较为简单的函数类问题，根据题目所给条件，利用观察法我们就可以快速地分析出此题重点考查学生算术平方根的性质，随后再根据算术平方根的性质即可正确解题.

2 函数单调性法

例2求解函数f（x）=3ln的定义域及值域.

解析

点评判断函数的单调性有多种方法，学生可以使用定义法直接判断所给函数在给定区间是否单调，同时还可利用复合函数分析法，由“同增异减”来确定函数单调性.另外，针对较为常见的函数，学生也可以利用图象法来判断函数的单调性.

3 反函数求解法

例3求解函数的值域.

解析

点评

反函数在高中阶段并不常用，但教师在教学过程中要引导学生掌握一定的反函数基础，为进一步的数学学习奠定基础.

4 数形结合法

数形结合法是一种重要的解题方法，教师在日常的数学教学中可以借助现代化信息技术，培养学生应用数形结合思想解题的思维.例如利用几何画板等软件为学生展示标准图形，让学生更加直观清晰地了解函数图象的变化过程，加深学生对于函数作图步骤的印象，从而有效提升学生的解题效率.

5 巧用对称性

常见的对称类型函数包括：过原点的一次函数、三次函数（其函数图形为中心对称图形），正弦、余弦函数（其函数图象为轴对称图形）……

例4若函数f（x）=2sin（2x+t-）（0＜t＜π）是偶函数，求t的值.

解析

方法1定义法

因为f（x）为偶函数，所以对任意实数x，f（-x）=f（x）恒成立.

从而我们可以得到

方法2巧用对称性

因为f（x）为偶函数，所以函数y=f（x）的图象关于x=0对称.所以，当x=0时，函数f（x）取得最

点评根据题目所给信息，将偶函数问题转化成对称问题，再利用三角函数特殊的对称性来解决问题，进而可以显著减少解题运算量，帮助学生更好地理解数形结合思想的本质.

6 三角换元法

三角换元法是高中阶段数学教师应逐步引导学生形成、领会的一个重要的解题方法.

例5已知函数，求函 数f（x）的定义域及值域.

解析

由算数平方根的性质得6-x≥0并且6x≥0，我们可以很容易地得出f（x）的定义域为［0，6］.

易知f（x）≥0，令x=6sin2t，其中t 的取值范围为代入f（x）表达式得

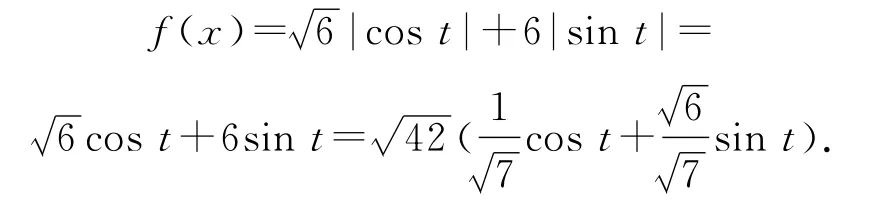
点评

利用三角函数sin2x+cos2x=1 的性质，采取三角函数的特殊换元形式对根式下的内容进行化简，进一步降低了数学计算的复杂性，提高了学生数学解题的正确率.

7 结语

作为高考数学的重要题型之一，函数知识是学生高中阶段数学知识学习的重点，同样也是难点，并且贯穿于整个高中数学知识学习中，在高中数学各个知识点之间起着重要的衔接作用.因此，掌握多样化的函数题解题技巧，利用多种思维方式求解与函数有关的题目，不仅对于发展学生的创新思维能力、实际应用能力等具有极其重要的作用，同样也对提升学生的数学学科核心素养具有极其重要的价值.