例谈高中数学中数列递推问题的处理方法

◇ 安徽 黄振东

数列是高中数学的重要知识点，但学生遇到较为复杂的递推问题时，常常不知道如何下手，失分率较高.为避免这一情况的发生，教学中应注重筛选经典的例题，为学生讲解数列递推问题的处理方法，使学生掌握相关的解题技巧，实现快速解题.

1 新定义递推问题

这类问题在高考中经常出现，主要考查学生的分析应用能力.解题时应深入理解题干，根据要求解的问题灵活应用数列通项公式的递推方法.

例1设数列｛an｝满足a1=2，an+1=an+2（n+1），若［x］表示不超过x 的最大整数（如［1.6］=1，［-1.6］=-2），则

A.2020 B.2019 C.2018 D.2017

解析

由已知条件an+1=an+2（n+1），可推出an+1-an=2（n+1），又因为a1=2，则an=（an-an-1）+（an-1-an-2）+…+（a2-a1）+a1=2n+2（n-1）+2（n-2）+…+4+2=n（n+1），则因此=2+1+1+…+1=2019，故选B.

2 奇偶项通项公式不同问题

高中数列问题中有一部分数列奇偶项的通项公式不同，问题难度较大.解答时需要进行分类，找到奇数项与偶数项之间的关系，再正确求解奇数项与偶数项的通项公式.

例2已知数列｛an｝的前n 项和Sn满足Sn-则S100=（ ）.

解析

很多学生看到该题不知如何下手.事实上在突破该类问题时仍然需要应用所学的基础知识，找到奇数项与偶项数之间的递归关系.

因为数列｛an｝的前n 项和Sn满足

当n≥2时，得

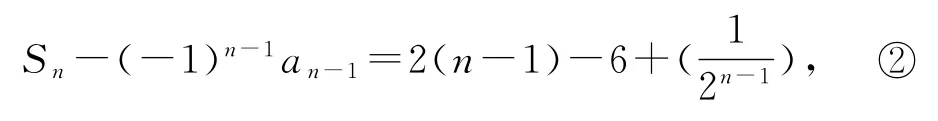
①-②得an-（-1）nan+（-1）n-1an-1=2-，所以当n 为偶数 时即n=102时，当n 为奇数时101时，2a101+a100=，因此，，即S100=a100+200-6+=200，故选B.

3 两个数列问题

高中数列的部分习题涉及两个数列，解答该类问题有时需要求解出其中一个数列的通项公式，有时则需要找到两个数列之间的关系.

例3已知数列｛an｝满足a1==+3an+1，若，设数列｛bn｝的前n 项和为Sn，则使得｜S2019-k｜最小的整数k 的值为（ ）.

A.0 B.1 C.2 D.3

解析

由an+1=an2+3an+1，可得an+1-an=+2an+1=（an+1）2≥0，故数列｛an｝为递增数列，而an+1+1=+3an+2=（an+1）（an+2），因 此，，则，则

高中数列递推问题难度较大，教学中教师应注重筛选经典例题，为学生深入细致地讲解，同时组织学生开展相关的训练活动，使学生真正地掌握相关的解题技巧，提升学习能力.