基于加权构造链表的频繁加权项集挖掘算法
文 凯,许萌萌,耿小海
(1.重庆邮电大学 通信与信息工程学院,重庆 400065;2.重庆邮电大学 通信新技术应用研究中心,重庆 400065;3.重庆信科设计有限公司,重庆 401121)
0 引 言
频繁项集(FIs)是数据挖掘领域的一个重要研究内容。近年来,由于挖掘需求和任务不同,频繁项集的挖掘可分为频繁闭项集[1]、top-rank-k频繁项集[2]、可擦除项集[3]、最大频繁项集[4]等,并为此提出了很多有效的数据结构,包括Node-list、Nodeset、N-list[5]以及B-list[6]等。
FIs挖掘算法应用广泛,如购物篮数据分析、智能系统[7]等,但其往往只关注项集外观而忽略项集重要性。为发现加权数据库价值,频繁加权项集挖掘(FWIs)算法应运而生。Lee等[8]提出了FWI*WSD和FWI*TCD算法,它们使用带有二维数组的新型前缀树结构来存储和压缩数据库信息,以此挖掘FWIs。但其扫描数据库多次,处理大数据库时时间消耗大。Lan等[9]提出PWAI算法,使用最大序列模型来收紧子序列加权支持度的上边界,减少挖掘中的候选个数。而WIT-FWIs-Diff算法是采用WIT-tree并结合Diffset策略来挖掘FWIs的算法。Nguyen等[10]利用IWS结构来存储和处理标识符集合,通过消除交易集中位向量表示的所有0-字来减少内存消耗,并创建映射数组,以更快地计算项集的加权支持度,提高FWIs的挖掘效率。
本文提出了BFWI算法,将项集信息完整地压缩到构建出的WB-tree中,以集合枚举树为搜索空间来保证所挖掘项集的完整性,采用包含索引避免复杂的项集连接以减少连接次数,并结合超集等价性质加快确定FWIs的加权支持度,以此来提高算法的时间效率,减少内存消耗。
1 相关知识
1.1 基本概念
定义1 加权数据库WD:给定一数据库交易集,其表示为T={t1,t2,…,tm},I={i1,i2,…,in} 是由n个不同项组成的集合,其中ik(k=1,2,…,n) 表示项。集合I中对应项的权重由w={w1,w2,…,wn} 表示。WD是由
定义2 交易集的权重tw:交易集tk的权重表示如式(1)所示,其中∑ix∈tkwx为tk项权重之和, |tk| 为tk中项的数量
(1)
定义3 加权支持度ws:设项集X={i1,i2,…,ik},ij的权值是wj(0≤wj≤1), 则X的ws如式(2)所示,t(X)为包含X的交易集合
(2)
定义4 FWIs:已知用户给定的minws阈值,若某一项集的ws不小于minws,则称这样的项集为FWIs,即频繁加权项集。从WD中挖掘FWIs的问题主要是找到满足minws的所有FWIs。
1.2 B-list结构
B-list结构是在BTK算法中为挖掘top-rank-kFIs而提出的,该结构将数据库信息压缩到只需扫描一次即可建树完成的TB-tree中。B-list结构还可挖掘FIs,如BLFPM算法[11],以及最大频繁项集,如BMFI算法。
近些年,研究者通常改进数据结构来提高FIs的挖掘效率。N-list结构[12]计算交集的速度快,但不宜两个短项集求交来生成更长项集。DiffNodeset结构[13]利用差集计算Nodeset,但其工作在数量较大的叶子节点集上。在挖掘FIs方面B-list结构具有许多优点。①事务数据库被压缩到树中,因此B-list的存储空间很小且节点信息只需一次扫描即可得到。②B-list结构可计算项集支持度,减少运算过程。③利用线性复杂度的交叉算子,可快速确定k-项集(k>2)的B-list。而其扩展结构WB-list也具此类优点。
2 BFWI算法
2.1 加权构造树(WB-tree)和节点(WB-code)
传统算法通常将信息压缩到PPC-tree、FP-tree中,存在多次扫描效率低下的问题。因此BFWI算法采用一次扫描即可获得各节点开始和结束建立的全部信息的WB-tree结构。
定义5 WB-tree:加权构造树是由根节点“Root”和一系列作为根节点子树的项前缀树组成。项前缀树的各个节点信息由item-name, weight, parent-pointer, start-build和finish-build共5部分组成。其中item-name存储当前节点的名称,weight是通过该节点的tw值之和。parent-pointer是该节点指向父节点的指针。start-build和finish-build分别存储一个v值和w值,v表示树开始构建时的第v个节点,w表示树完成构建时的第w个节点。
由定义5,WB-tree的构造过程如算法1所示。
算法1: Build-WB-tree(WD,minws)
输入: WD,minws
输出: the corresponding WB-tree,F1
(1) Scan WD and calculatetw,wsof the 1-itemsets andsumtw
(2) Find out the set of 1-itemsets withws≥minws,F1, sort the element in descending order of theirwsvalues
(3) Build a root node named ‘Root’, initialize global variablestart=0,finish=0
(4)foreach different first itempin DBdo//pandqare the itemsets of WD, Node is the node of WB-tree
(5) CallWeightBuildTree(p, Node) to insertpinto WB-tree
(6)endfor
(7)end
functionWeightBuildTree(p, parent)
(1) LetTPbe a list of transactions in DB which contain prefixp
(2) Build a new nodeN∶N.name = name of the last item inp;N.weight=thesumoftwvalues of transactions passing throughN;N.parent = parent
(3)N.start = ++start
(4)foreach different first itemqinTPdo
(5) CallWeightBuildTree(p∪q,N)
(6)endfor
(7)N.finish = ++finish
(8)end
性质1 设m、n是WB-tree中两不同节点,其对应WB-code依次为
WB-code是不会丢失节点信息的数据库压缩内容。若已知两节点s和f,由性质1可快速判定两者的祖孙关系,加快挖掘FWIs的进程。
2.2 加权构造链表(WB-list)
定义6 WB-list:给定WB-tree,项集X的WB-list是由形如 <(s1,f1,w1),(s2,f2,w2),…,(sn,fn,wn)> 的WB-code组成的序列,并按s升序排序,其序列中的每个
定义7k-项集的WB-list:设PX和PY是两个 (k-1)-项集,有相同前缀P(P可为空),根据F1的顺序,X在Y之后,WBL(PX)、WBL(PY)、WBL(PXY)分别是PX、PY、PXY的WB-list,则WBL(PXY)由以下决定:
(1)对每个WB-code,Ci(si,fi,wi)∈WBL(PX) 和Cj(sj,fj,wj)∈WBL(PY), 若Cj是Ci的祖先,则将 (sj,fj,wi) 添加到WBL(PXY);
(2)遍历WBL(PXY), 将具有相同(s,f)信息的节点进行合并得到新WB-code,其权值为这些WB-code的权值之和。
性质2 给定一项集P=X1X2…Xn,Xi在Xi+1后面(按F1的排序),且P的WB-list是WBL(P)={(s1,f1,w1),(s2,f2,w2),…,(sm,fm,wm)}, 则项集P的ws计算如下
(3)
证明:设
(4)
假设T(P)为包含P的交易集,则由条件①可得
(5)
由定义3知
(6)
由式(4)和式(5)可得式(7),性质2由此得证
(7)
性质3 给定一项集P和项X,X∉P,若ws(P)=ws(P∪{X}), 对于任一个满足S∩P=∅且X∉S条件的项集S,都有ws(S∪P)=ws(S∪P∪{X})。
证明:由于ws(P)=ws(P∪{X}), 则对任意包含P的项集必然包含项X,所以对于S∪P的项集也必包含项X,即ws(S∪P)=ws(S∪P∪{X})。
采用性质3可很大程度地减少搜索空间,图1是以c,e,d,a,f为示例构造的集合枚举树。构造过程见文献[5]。
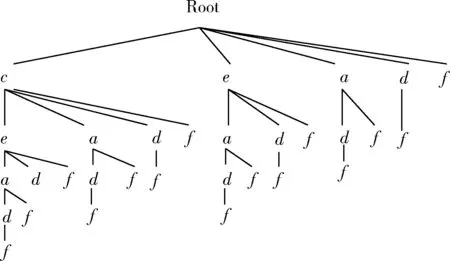
图1 示例集合枚举树
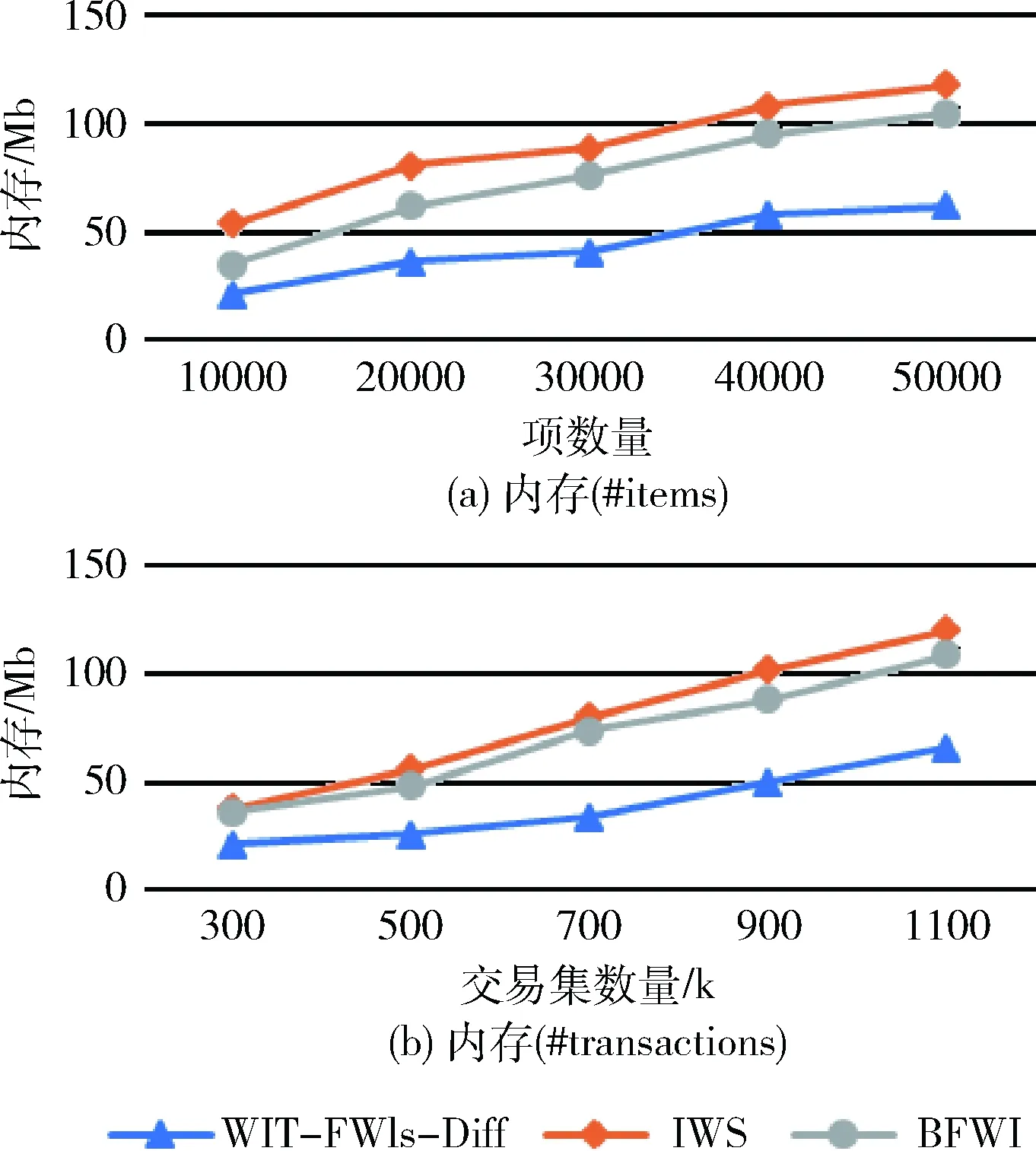
性质4 假设已知频繁k-项集P的WB-list,WBL(P)={(s1,f1,w1),(s2,f2,w2),…,(sm,fm,wm)}, 则s1 证明:由于项集的WB-list是按WB-code中s的升序排列,因此s1 由定义7,可对两(k-1)-项集求交得到k-项集的WB-list,求交集如算法2。根据算法2,WB-list交集的时间复杂度为O(l),其中l是最大长度的WB-list。以PX和PY的WB-list,Ci(s1i,f1i,w1i) 和Cj(s2j,f2j,w2j) 为例,用性质1判断子孙关系,若Cj为Ci的祖先,则将 (s2j,f2j,w1i) 插入到PXY的WB-list中。伪代码(5)-(12)行使用性质4来减少求WB-list交集的复杂度。如当s2j 算法2: Function WB-Intersection(WBLA,WBLB) 输入:PA、PB的WB-list,WBLA={(s11,f11,w11),(s12,f12,w12), …, (s1m,f1m,w1m)},WBLB={(s21,f21,w21),(s22,f22,w22),…,(s2n,f2n,w2n)},minws 输出:WBLC={(s31,f31,w31),(s32,f32,w32),…,(s3r,f3r,w3r)} 和ws//交集PAB的WB-list (1)WBLC←null (2) leti=0;j=0;r=0 (3)sum=ws(PA)+ws(PB)//sumis used to judge the ending (4)while(i≤mandj≤n)do//m和n分别为WBLA和WBLB的长度 (5)if(s1i>s2j)then (6)if(f1i (7)if(|WBLC|>0) and (s2j=s3r)thenw3r+=w1i (8)elser++; add (s2j,f2j,w1i) intoWBLC;i++ (9)elsesum=sum-w2j;j++ (10)elsesum=sum-w1i;i++ (11)ifsum (12) returnWBLC 定义8 包含索引:频繁项集A的包含索引用 subsume(A) 表示,即 subsume(A)={B∈F1|g(A)⊆g(B)} (8) 其中,g(A)表示项集A的事务集合。 性质5 设项集A包含索引为subsume(A)={A1,A2,…,Am}, 则 {A1,A2,…,Am} 与A相结合的2m-1非空子集的每个ws等于A的ws。证明参见文献[12]。 本文将包含索引与项集求交方法结合,通过将F1与不是其包含索引的F1进行连接合并,即可获得频繁候选2-项集,接着使用算法2产生k-FWIs;对含包含索引的F1,只需将之与其包含索引合并而无需计算ws,合并后的ws等于它本身的ws。利用包含索引减少了频繁2-项集的连接次数,不需产生项集与其包含索引子集结合的候选项,并结合性质3来减少计算k-FWIs的k(>2)时间,从而提高了算法效率。 从以上基础,本文提出挖掘FWIs的BFWI算法。算法具体流程如图2所示,步骤如下: (1)使用算法1构造WB-tree,并根据已定义的minws产生F1及其对应的WB-list; (2)获取所有1-项集的包含索引; (3)将包含索引与之对应的F1直接合并可得到F2,并将其插入到结果当中,其ws为F1的ws; (4)遍历集合枚举树并通过利用算法2对两(k-1)-项集的WB-list求交集以确定k-FWIs。将A与其包含索引根据性质5合并,与A相结合的2m-1非空子集的每个ws等于A的ws;在某些情况下,使用性质3可快速确定项集的ws值,而不需要计算项集的WB-list,从而减少了搜索空间; (5)重复步骤(4),直到无新的(k+1)-FWIs产生。 图2 BFWI算法流程 为验证本算法有效性,将BFWI算法与IWS和WIT-FWIs-Diff算法就运行时间和内存两方面进行对比。实验环境为Inter(R) Core(TM) i5 3337U @ 1.80 GHz CPU,内存4 GB,64位操作系统。用Java语言在同一机器上实现这3种算法,采用的测试集来自http://fimi.cs.helsinki.fi/data。实验所测试的4个数据库特性见表1。 表1 测试数据集特性 其中#Trans是事务集数目,#Items是项数目,Avg.Length是交易集平均长度。Spare level为数据稀疏性,值越小说明数据稀疏性越大。实验通过改变minws来记录算法的运行时间和内存占用情况,其中运行时间和内存占用分别如图3和图4所示。 图3 运行时间对比 图4 内存占用对比 如第3节所示,BFWI算法首先构建WB-tree,对于每个事务,删除不满足minws的项,其余项在WB-tree中进行排序和压缩。由下闭包属性,删除一个低于minws的项对整个结果没有影响。其次算法遍历WB-tree生成F1的WB-list,并将FWIs的信息存储于内。由性质1,值对(si,fi)在树中保持子孙关系,wi值则存储压缩在树中的事务集权值之和(性质2)。最后算法通过遍历和检查集合枚举树来挖掘FWIs,分别从F1集合开始,依次确定F2、F3等。原则上集合枚举树包含F1生成的所有子集,由此在遍历枚举树时不会遗漏任何情况,且基于性质3,算法可找出不需执行WB-list交集的WFIs。从以上分析,BFWI算法完全保证了FWIs的完整性和正确性。 图3是BFWI算法与IWS和WIT-FWIs-Diff算法在不同数据集上运行时间的比较。为减少算法运行时间之间的差距,纵坐标采用对数刻度(lb)。分析可知:在稠密数据集上,WIT-FWIs-Diff算法消耗时间较少,但在稀疏数据集上则较多。而IWS算法则相反,原因是IWS算法删除了tidset位向量表示中的所有0-字,因此IWS算法在稀疏数据集上有着较好的时间效果。总体来说,3种算法的运行时间都随minws的降低而增大,但IWS和WIT-FWIs-Diff算法的运行时间始终高于BFWI算法,表明BFWI算法有较高的时间效率。 图4是BFWI算法与其它两算法内存占用的对比。分析可知:BFWI算法在稠密和稀疏数据集上占用的内存都较少,表明该算法具有较好的空间效率。原因是BFWI算法中的WB-tree简单且高度压缩,改进的求交算法减少了计算项集ws的过程,加快确定k-FWIs。删除非频繁项缩小搜索空间,从而减少内存消耗。但当minws很低且在大而稀疏的数据集上如Retail和Kosarak(如图4(c)和图4(d)所示),BFWI算法的效率比消除0-字的IWS算法略差。 图5是在可伸缩性方面的内存消耗,可知WIT-FWIs-Diff效果最好,而 BFWI算法在构建WB-tree时需存储开始和结束建立的节点信息,随着项和交易集数量的增多,存储的节点信息量增多,内存占用也越来越大。如图5(b)中,当交易集数量从300 k到1100 k时,BFWI的内存增加了3倍,接近WIT-FWIs-Diff(3.1倍)和IWS(3.2倍)内存的增加。因此,BFWI算法在其内存占用可接受的范围下,具有良好的运行时间效果。 图5 内存可伸缩性 本文提出了一种新树结构WB-tree,该树简单且具高压缩性,由此提出BFWI算法。BFWI算法通过使用集合枚举树作为搜索空间,以防止漏掉项集;利用包含索引来减少2-项集的连接次数,提高了时间效率;并结合改进的WB-list求交集算法和超级等价性质,降低算法时间复杂度,以快速确定加权频繁k-项集,提高算法效率。实验结果表明,BFWI算法的性能在不同的数据集中均优于IWS和WIT-FWIs-Diff算法。根据不同的挖掘任务和需求,加权可擦除项集将会是下一步的研究方向。2.3 改进的WB-list交集
2.4 基于包含索引的频繁2-项集挖掘
3 算法描述
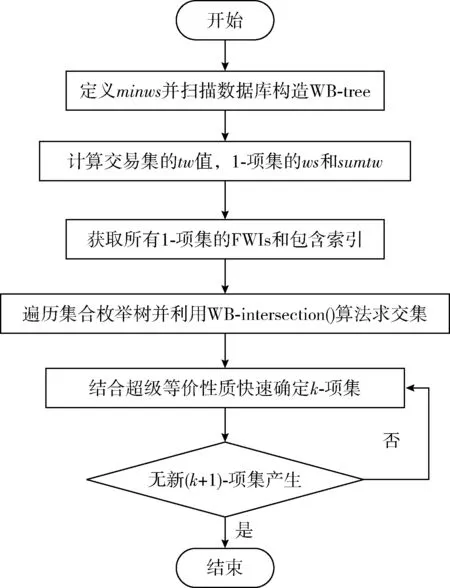
4 实验结果分析
4.1 算法的完整性和准确性
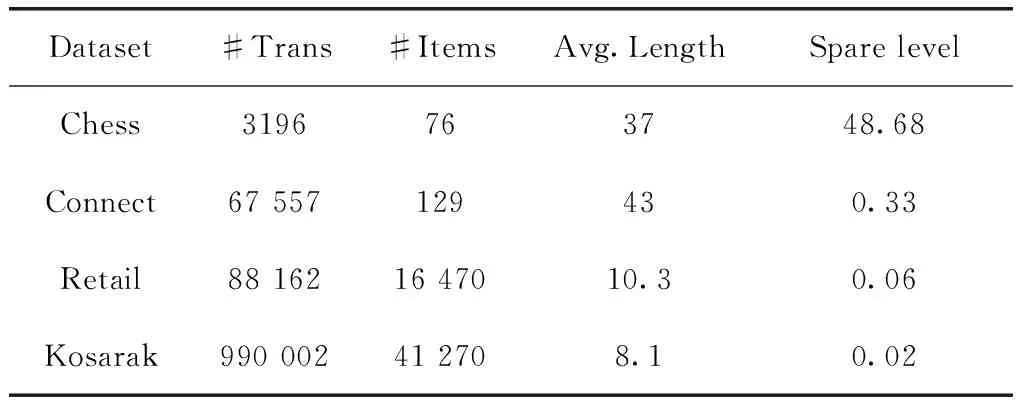
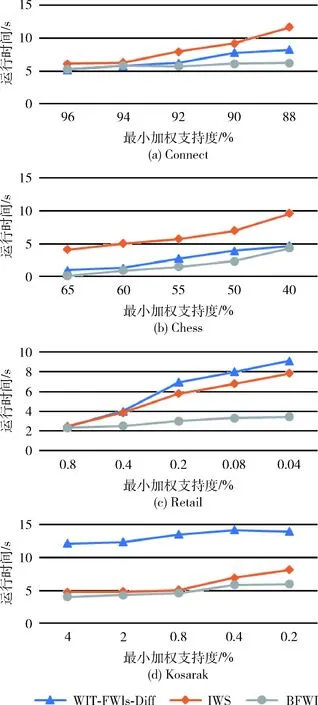

4.2 时间和内存对比
4.3 实验效果分析
5 结束语

