基于相邻像素间比特置乱的图像加密算法

郭 媛，敬世伟，周艳艳

(齐齐哈尔大学 计算机与控制工程学院，黑龙江 齐齐哈尔 161006)

0 引 言

图像信息具有直观生动形象的特性被广泛运用，其安全性受到大量学者关注[1-5]。其中陈关荣等[5]提出了像素置乱和异或扩散的加密算法，很好满足了香农提出的加密算法应具有的混淆和扩散原则。但由于混沌序列与明文无关联，导致加密方法被选择明密文攻击破译[6,7]。由此邓晓衡等[8-12]在文献[5]的基础上提出比特置乱加密算法，既保留了原算法的优点，又通过比特置乱进一步改变像素值，更好掩盖明文统计特性，同时将混沌序列与明文产生关联，使得中间密钥随明文自适应变化，能较为有效抵御选择明(密)文攻击。但上述加密方法仍存在以下两个问题：比特置乱环节所用混沌序列不敏感；对选择明文攻击防御力弱。文献[8-10]加密算法虽有不同，但都是对单一像素点八位二进制数置乱，使得一个像素点0 bit和1 bit的比重不变[14]。这引起所用混沌序列不敏感，即只进行扩散和全局置乱的解密，就能看到原图的大体轮廓。并且在第三步加密过程中采用单向扩散，使其很容易被列方程组的方式破解，同时使用明文像素值总和与平均值作为明文与混沌序列的联系，关联性不强被文献[15]破解。文献[11-13]提出一种比特置乱方式，虽然解决了比特置乱模板不敏感问题，但比特置乱方式较为复杂，且仍未改变明文关联方式易受到选择明文攻击[16]。

对此本文提出一种相邻像素间比特置乱方式，相邻两像素点间16位二进制数的置乱，充分利用了全局置乱后相邻像素点间的相关性被完全打破的特性，解决单一像素点二进制下置乱所用混沌序列不敏感问题。正反双向不同密钥扩散克服了文献[15,16]用列方程组的方式破解扩散中间密钥序列的问题，同时两个混沌序列和扩散的初值都由明文的SHA-256哈希值算出，明文哈希值比明文像素值总和、平均值对明文变化更为敏感，使得本文抗选择明文(密文)攻击更强，明文敏感性更好。

1 基本原理

本文提出的算法是将明文经过像素位置的全局置乱、比特置乱和正反双向不同混沌序列扩散处理得到密文，其中选择用明文的SHA-256值作为明文与随机序列关联的值，使得中间密钥随明文自适应变化。解密过程是加密过程的逆过程，其中全局置乱操作加解密完全相同。本文加解密过程如图1所示。

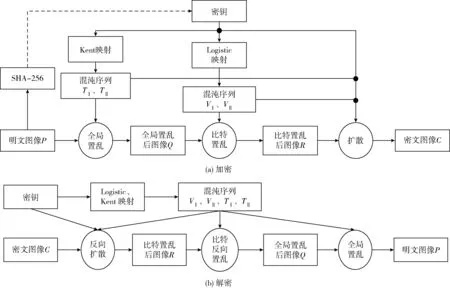
图1 加解密过程

由于Kent和Logistic映射是简单快速易于实现的两种映射，同时还具有很好的混沌特性，故本文采用这两种映射。Kent的映射关系为

(1)

其中，混沌控制参数s∈(0,1)， 序列值x∈(0,1)。 Logistic映射表达式为

xn+1=μxn(1-xn)

(2)

式中：序列值x∈(0,1)， 参数μ∈(3.57,4] 时整个映射处于混沌状态。

2 加密过程

2.1 初始值产生

步骤1 读取数字图像Pm*n，并求出明文图像P的SHA-256值H={H1,H2,……,H64}。

步骤2 由式(3)～式(5)计算出Kent和Logistic映射初值x0、y0以及异或扩散时初值C0

(3)

(4)

(5)

2.2 像素位置全局置乱

步骤1 设定Kent映射控制参数s=0.55，并将用式(3)算出的初值x0带入式(1)产生长度为2*m*n+1000的序列，丢掉前1000个迭代值以消除暂态效应的影响，得到一个长度为2*m*n的序列T={T1,T2,……,T2*m*n}。 并分成TI={T1,T2,……,Tm*n} 和TII={Tm*n+1,Tm*n+2,……,T2*m*n} 分别用于全局置乱和反向扩散。

步骤2 将TI按从小到大顺序排列，并用一个序列T′={T′1,T′2,……,T′m*n} 记录排序后对应点在TI中的位置。

步骤3 将图像矩阵Pm*n按行优先的顺序转换为一维序列P′={P′1,P′2,……,P′m*n}。

步骤4 将P′按式(6)进行全局置乱得到置乱后的序列Q

Qi=P′T′i

(6)

2.3 相邻像素比特置乱

步骤1 设定Logistic映射控制参数μ=3.99，并将用式(4)算出的初值y0带入式(2)产生长度为2*m*n+1000的序列，丢掉前1000个迭代值以消除暂态效应的影响得到一个长度为2*m*n的序列V={V1,V2,……,V2*m*n}。 并分成VI={V1,V2,……,Vm*n-1} 和VII={Vm*n+1,Vm*n+2,……,V2*m*n} 分别用于比特置乱和正向扩散。

步骤2 将全局置乱后的序列Q转化为二进制数得到矩阵mn*8的矩阵R′i,j。 通过对应序列VIi的大小决定R矩阵对应i和i+1行的置乱方式。交换过程如图2所示。

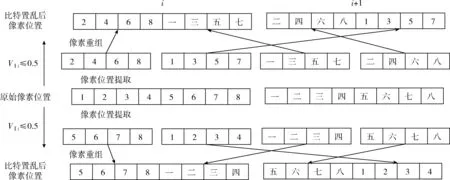
图2 比特交换原理

步骤3 将经过比特置乱后的序列转换为十进制得到比特置乱后的图像R。

2.4 正反双向不同混沌序列扩散操作

步骤1 将混沌序列VII、TII经过式(7)处理得到值在[0,255]之间的序列V′、T″

x′i=mod(xi×108,256),i=1,2,……,m*n

(7)

步骤2 对比特置乱后的R由式(8)进行正向扩散处理得到C′,其中C0由式(5)求得

(8)

步骤3 正向扩散处理得到的C′由式(9)进行反方向扩散处理得到C″,最后将C″转换为m*n密文矩阵C

(9)

3 解密算法

解密过程是加密过程的逆过程，如图1(b)所示。首先，将密文C中的值分别按式(10),式(11)进行反向扩散得R

(10)

(11)

将Ri转化为二进制，利用Vi将二进制数比特反向置乱，再转化为十进制可得置乱后图像序列Q,最后将Q进行全局置乱即可得到明文图像P。

4 算法实验性能对比分析

选取Lena(256×256)灰度图像在matlab2016a环境下进行实验仿真。设置Kent和Logistic映射控制参数s=0.55、μ=3.99，两映射初值和C0由算法求得。由图3可见密文中完全看不出明文信息。下面将对算法的比特置乱混沌序列敏感性、选择明(密)文攻击、抗差分攻击、统计特性和密钥空间进行分析对比。

图3 加解密效果

4.1 混沌序列敏感性分析

针对单一像素点比特置乱对比特置乱环节所用混沌序列不敏感，即在解密过程中不进行比特置乱解密也可看见明文信息问题。本文充分利用像素位置全局置乱后两像素相关性极低这一特性，在相邻两像素点间进行比特置乱，很好解决了上述问题，本文提出加密算法和文献[8,9,12]在解密过程中不解比特置乱过程的解密图对比如图4所示。

图4 比特置乱所用混沌序列敏感性分析

由图4可见，文献[8,9,12]不对比特置乱解密的图像依旧能看到明文图像的大致轮廓，本文提出的加密方案却完全看不出明文信息。故本文的加密方案对比特置乱的混沌序列敏感性更好，更适合用于图像加密。

4.2 抗选择明(密)文攻击分析

选择明(密)文攻击指攻击者选定一些特殊的明(密)文，放入加密(解密)系统中得到一些明密文对，从而推导出等价的中间密钥。

由图5分析可知破解关键在于文献[9]后两步加密的混沌序列未与明文产生关联，而第一步加密的混沌序列以明文的均值作为联系方式。本文加密算法针对选择明文攻击在以下三方面进行了加强：①将所用混沌均进行了关联，使得用特殊像素值方式求出的中间密钥与待破解的密文对应的中间密钥不同，而失去作用；②本文用哈希值作为明文与混沌序列的联系，由于哈希算法的单向性[17]，在第三步破解中，用密文反解后两步得到全局扩散后的图像得不到明文哈希值，同时也找不到一个哈希值相同且只有一个点为0的图像；③用双向不同混沌序列的扩散，解决以列方程组得到中间密文问题。

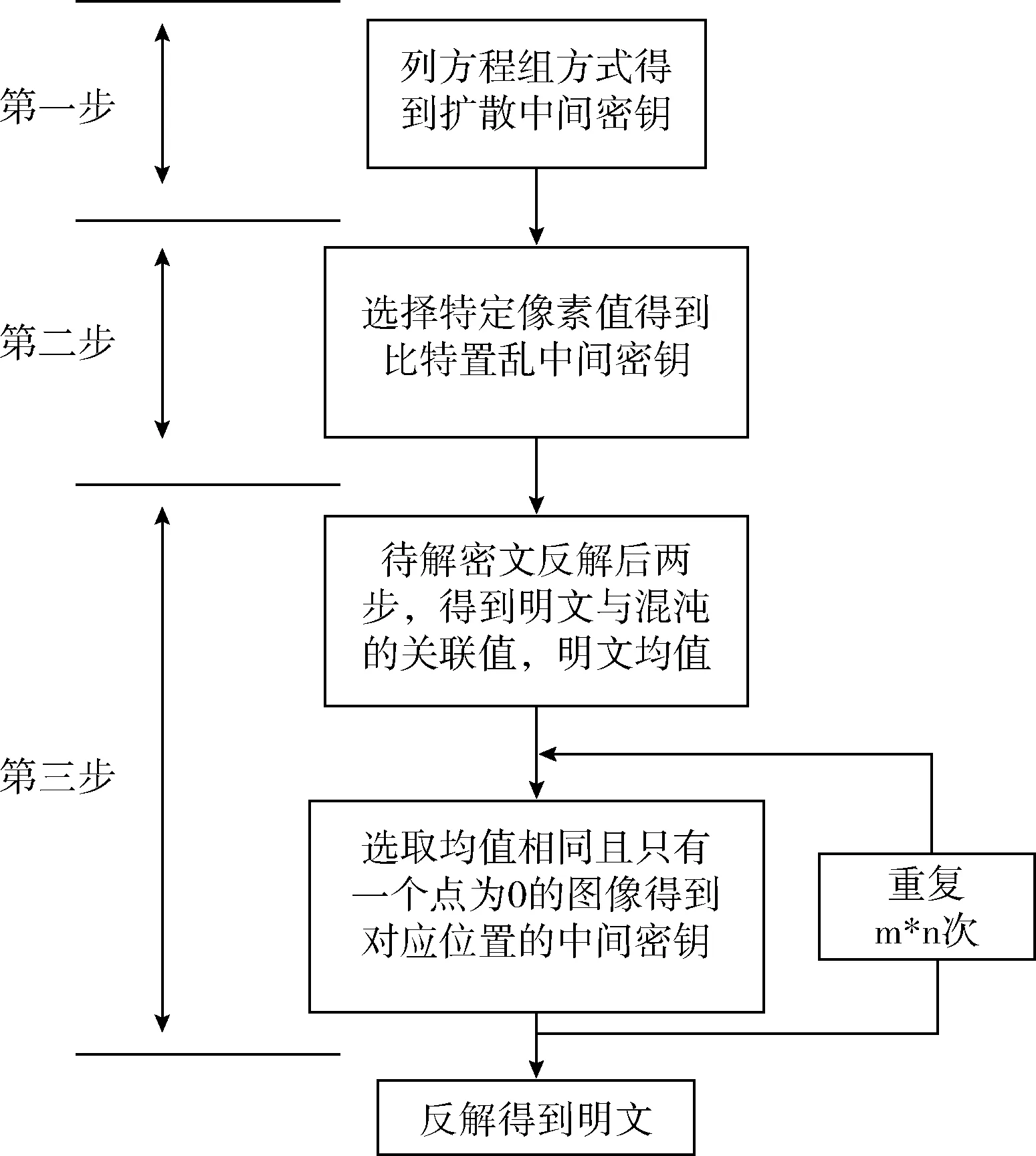
图5 文献[15]对文献[9]破解步骤

在明文未与扩散所用混沌序列关联情况下，运用方程组思想求解本文中间密钥，设扩散所用的中间序列设为A、D和初值C0。B1和B2分别为像素全为0和255的图像对应正向扩散密文C1′、C2′，和密文C1、C2。由于前两步加密对B1、B2没有影响所以

(12)

(13)

其中，C10=C0、C20=C0、C2m*n+1=C0、C2m*n+1=C0由式(12)、式(13)可知共4*m*n个方程式，由于不知中间密文C1′、C2′，故共有4*m*n+1个未知数，而解不出中间序列A、D和初值C0。所以本文不能用解方程组的形式来破解扩散时的中间序列。故本文所用的正反双向不同密钥的加密方式比单向在抗选择明文攻击时更强。

4.3 抗差分攻击

4.3.1 明文敏感性分析

好的加密算法明密文之间应该具有雪崩效应，即使明文发生细微变化，密文图像也应该有巨大变化。为此本文引入明文图像的SHA-256值作为混沌序列的初值。SHA-256比明文像素总和及均值更加敏感。如明文仅在第一个和第三个像素点(两像素点相差一)发生置换的情况下SHA-256就由65f8fc53cabb54d9ea7ab076271904289531ff4bebcd8543df9752ff5018f797变为了1b6162c66fe3a6367f51f529c76c95336946c72ef394ec1c9d579a5449d472d6，而明文的像素值总和却不变。本文运用像素值变化率(NPCR)和归一化平均变化强度(UACI)来定量分析明文敏感性。将明文图像、明文图像第一个像素点加一、和明文的第一三像素点交换位置进行加密得到C1、C2、C3，计算C1和C2、C1和C3的NPCR和UACI的值见表1。NPCR和UACI公式如下

(14)

(15)

其中，当C1(i,j)=C2(i,j) 时p(i,j)=0， 否则p(i,j)=1。

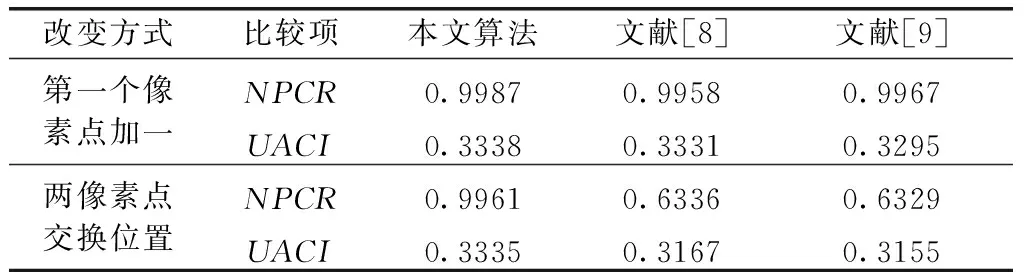
表1 NPCR和UACI值

由表1可见，本文像素变化率达到99%，说明本文在明文改变一个像素值的情况下，密文基本上每个像素值都得到了变化，同时值得注意的是当明文图像像素点位置发生微小变化时，文献[8,9]的密文变化就大幅降低，而本加密方法得到的密文完全不同。由此可见本算法更适合图像加密。

4.3.2 密钥敏感性分析

密钥敏感性指当密钥发生细微变化密文应完全不同，同样两个具有微小差别的密钥解密结果也应该不同。本文算法在密钥发生微小变化时，解密效果如图6所示。

图6 密钥偏差时的解密图像

由图6可见当密钥s，x0相差10-16时解不出原图像，当密钥s、x0相差10-17时成功解出原图，故s和x0的灵敏度为10-16。同理密钥y0和μ的灵敏度为10-15。由此可见，本文加密算法对密钥极其敏感。

4.4 统计特性分析

本文主要通过直方图和信息熵以及相邻像素的相关程度来分析算法的统计特性。

4.4.1 直方图与信息熵

直方图最能直观反映图像灰度值分布，信息熵能定量的分析。比特置乱后，以及最终密文的直方图如图7所示，其信息熵见表2

(16)

式中：pi为对应像素值出现的概率，一个系统越是混乱信息熵就越高，在int8型数据下理想值为8。

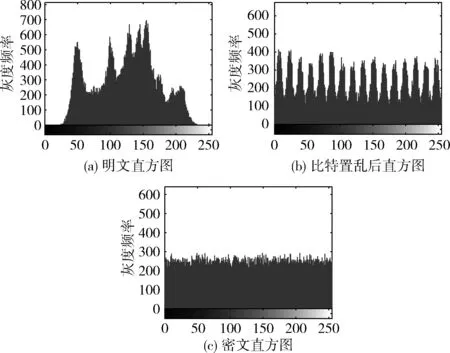
图7 直方图

由图7可见，明文图像的灰度值分布呈现出明显的分布统计规律，比特置乱后更平滑，密文已变得非常均匀，很好地隐藏了明文图像信息，留给密码分析者分析空间很小，能有效抵御统计分析攻击。通过表2信息熵对比可见本算法信息熵最接近理想值8，密文像素值分布最均匀，加密效果最好。

4.4.2 相邻像素的相关性

一个好的加密算法应该显著破坏相邻像素的相关性[18]。明密文的水平、垂直、对角方向的相邻像素的相关系数见表3。为在视觉上看出相邻像素相关性，画出本算法明密文在水平方向上的相关性如图8所示。相邻像素的相关系数公式如下

表2 信息熵对比

(17)

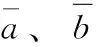
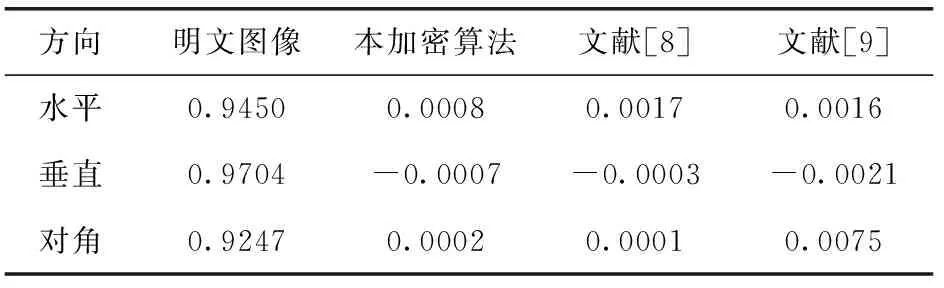
表3 密文图像像素相关系数

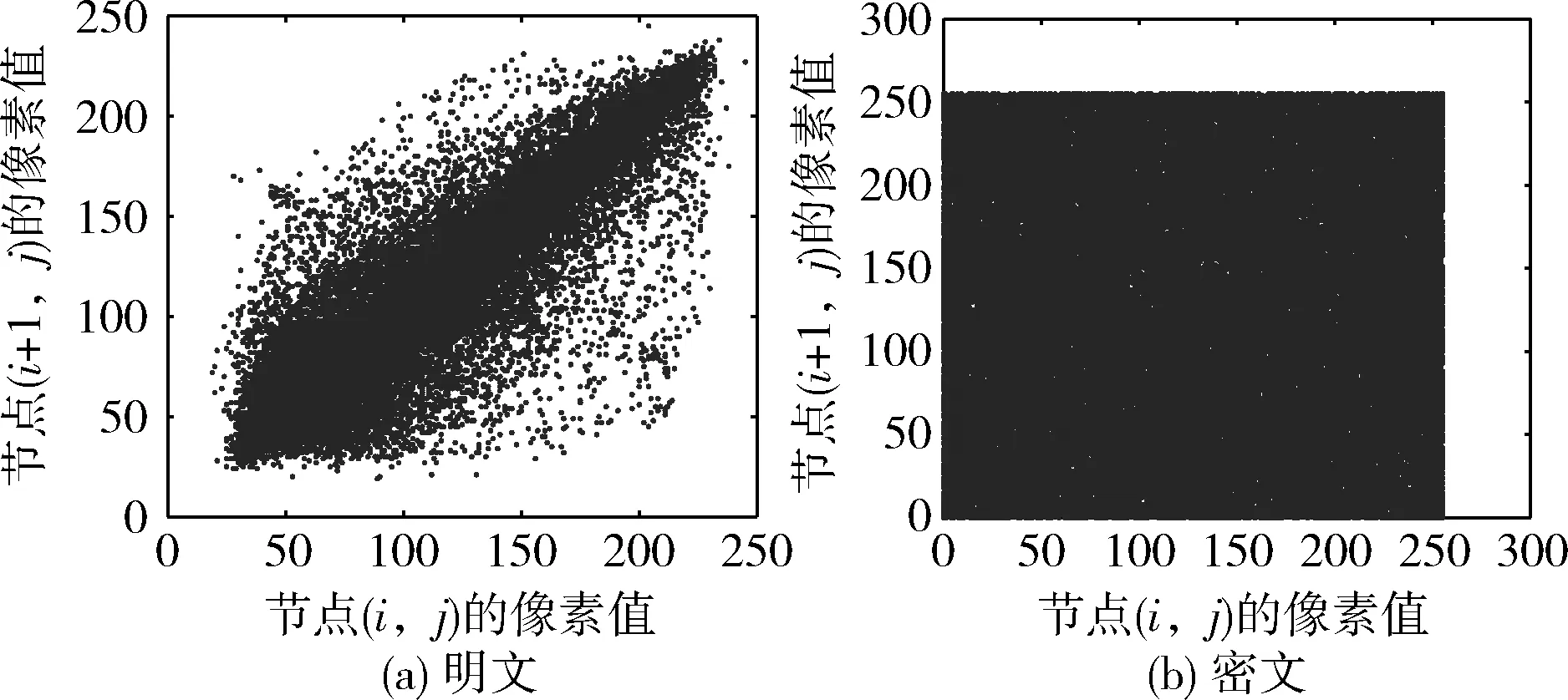
图8 明文和密文水平方向上的相邻像素分布

由图8可知明文图像的相邻两点大部分都几乎相等，密文图像就分布就非常均匀，相邻像素相关性就极低。表3也可见明文图像的相邻相关系数接近1，而密文图像的接近于0，相比于其它对比文献本文具有更小的相邻像素相关系数，说明本文在密文的相邻像素相关性上表现更好。

4.5 密钥空间分析

本文的密钥为Kent和Logistic映射的初值x0、y0和控制参数s、μ。每个初始密钥都采用双精度数据，保留小数后15位有效数字。本文的密钥空间至少是1060。本加密算法也可以将去掉混沌序列前n项值作为密钥，从而使得密钥进一步扩大。从安全的角度，密钥空间≥2100≈1030就能满足较高的安全级别，所以本算法的密钥空间对穷举攻击是安全的。

5 结束语

比特置乱加密算法不仅保留了“置乱-替代”加密算法的优点，同时强化了密码学性能，增加了密码系统的安全性和实用性，因此在图像加密中更具优势。但单一像素点进行比特置乱对所用的混沌序列不敏感；明文图像与混沌序列关联弱；对抵御选择明(密)文攻击效果不佳。由此本文提出了相邻两像素点间的比特置乱，充分利用了像素点置乱后的图像相关性极低这一特性，解决了单一像素点进行比特置乱对所用混沌序列不敏感问题，同时用正反双向不同混沌序列的扩散和用明文的哈希值算出加密过程中两个混沌序列和扩散的初值，很好抵御了选择明(密)文攻击，极大提升了明文敏感性。实验结果还表明本加密算法的密文分布均匀、相邻相关性低、密钥空间也足以抵御穷举攻击，因此本加密算法具有更好的应用前景。