群智感知系统中基于鲸鱼优化算法的任务分配
袁 姝,周朝荣,2+,杨正清,王婧柔
(1.四川师范大学 物理与电子工程学院,四川 成都 610101;2.成都信息工程大学 气象信息与信号处理四川省高校重点实验室,四川 成都 610225)
0 引 言
群智感知(crowdsensing,CS)[1,2]利用智能设备收集数据,提供了静态传感器网络难以支持的大规模应用服务,比如ParkSense[3]等。为了更好地支持各类应用服务,群智感知系统要求在某些约束条件下将任务分配给合适的工人,工人移动到对应位置执行任务,这样的任务分配问题是当前群智感知相关研究领域中的热点。
目前,已有学者针对群智感知系统中的任务分配问题展开研究。文献[4,5]考虑到任务的执行时长分配任务,但忽略了工人的在线时间限制。因此,针对工人在线时间存在限制的情况,文献[6,7]利用感知设备的可用时间代表工人的在线时间,从而分配任务。然而,工人的在线时间并非简单等同于感知设备的可用时间。为了避免此局限,文献[8,9]分别用工人活跃时间与最晚工作时间来表示工人的在线时间,但忽略了工人在线时间的不确定性。此外,考虑到工人的在线时间,则不能忽视工人的时间成本。虽然文献[10]考虑了预算对任务分配的影响,但预算中忽略了工人的延时成本与空闲成本。
为此,考虑工人在线时间为弹性时间的情况,采用模糊机会约束规划方法[11]对工人的在线时间进行建模,并引入延时成本与空闲成本。对应的任务分配问题为组合优化问题,属于NP-hard问题范畴,不存在时间有效的最优算法,只能考虑次优算法。鉴于鲸鱼优化算法(whale optimization algorithm,WOA)[12]具有全局搜索能力强等优点,利用WOA设计了两阶段算法求解该任务分配问题。仿真结果表明,所提出的算法与其它算法相比具有更好的搜索性能;同时,较之于固定在线时间,考虑弹性在线时间工人效率更高且工人成本更低。
1 问题描述与系统模型
考虑一个存在t个感知任务以及w个注册工人的群智感知系统。其中,T={T1,…,Tt} 以及W={W1,…,Ww} 分别表示任务集合与工人集合。对于任务i来说,TTi为该任务执行所需时间;对于工人j来说,WTj为该工人在注册时设定的预计在线时间。为便于问题的描述,给出以下定义。
定义1 任务执行时间MissionTime: 任务执行时间为工人执行系统所分配任务的总时间花费,其定义如式(1)所示
(1)
其中,Vj表示分配给工人j的任务集合。
定义2 空闲时间IdleTime: 工人在预计在线时间内未执行任务的时间称作空闲时间,其定义如式(2)所示
ITj=WTj-MTj
(2)
此时,WTj≥MTj。
定义3 延时时间DelayTime: 工人任务执行时间超过工人预计在线时间的情况下,工人实际在线时间即为工人任务执行时间,而工人超出预计在线时间的部分则为延时时间,其定义如式(3)所示
DTj=MTj-WTj
(3)
根据工人存在空闲时间定义工人空闲代价如式(4)所示
ICj=α*ITj
(4)
其中,α为单位空闲时间代价。
此外,根据工人存在延时时间定义工人延时代价如式(5)所示
DCj=β*DTj
(5)
其中,β为工人单位延时代价。
在任务分配之前,由于工人还没有开始执行任务,工人不能确定自己是否会在执行任务之后选择延长在线时间,此时,系统考虑工人均不延长在线时间,从而为工人初次分配任务。V′={V0′,V1′,V2′,V3′,…,Vw′} 表示此时感知任务的分配结果。其中,V0′为感知系统中未被分配的任务集合;V1′~Vw′分别表示感知系统为工人分配的任务集合。在这个阶段,由于系统考虑工人均不延长在线时间,工人的任务执行时间均不超过工人预计在线时间。此时,若工人存在空闲时间,则会产生空闲代价ICj′, 确定此时工人总代价(TotalCost)为
(6)
在初次任务分配之后,工人能够根据自身空闲情况以及后续安排决定是否考虑延长在线时间。此时,利用工人时间约束可能性(即工人不选择延长时间的可能性)及置信水平大小来表示工人最终是否选择延时。根据模糊机会约束规划方法,当工人时间约束可能性大于置信水平时,工人必须保证任务执行时间不超过预计在线时间,此时工人不选择延长在线时间来执行额外任务;而当工人时间约束可能性小于置信水平时,工人选择延长在线时间来执行额外任务,此时给工人分配额外任务。基于此,对初次任务分配的结果进行调整。集合V={V0,V1,V2,V3,…,Vw} 表示最终任务分配结果。同理,V0为最终任务分配后未被分配的任务集合;V1~Vw表示工人最终的任务分配集合。分配完成后,根据工人是否选择延时确定工人代价为延时代价或空闲代价
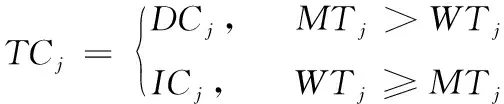
(7)
对应的工人效率也分为两种情况
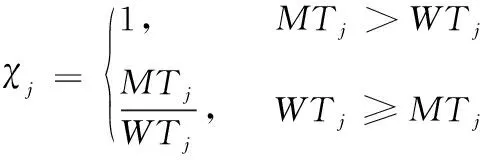
(8)
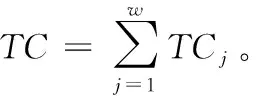
基于上述定义,考虑工人弹性在线时间的任务分配模型给出如下
(9)
约束条件
(10)
V0∪V1∪…∪Vw=T
(11)
V0∩Vj=∅,Wj∈W
(12)
Vk∩Vj=∅,j≠k
(13)
|Vj|≥1,Wj∈W
(14)
Cr(WTj-MTj≥0)>τ,Wj∈W
(15)
TC≤TC′
(16)
∃WTj,WTj-TTi≥0,Ti∈T,Wj∈W
(17)
其中,式(9)为优化目标即最大化工人总效率;式(10)与式(11)表示分配的任务为系统中发布的任务;式(12)与式(13)表示一个任务不能同时出现在工人任务集合以及未分配任务集合中;式(14)表示每个工人至少需要完成一个任务;式(15)为工人在线时间的模糊机会约束,其中τ为置信水平,采用模糊机会约束规划模型建模,在一定程度上允许工人实际在线时间超过工人预计在线时间;式(16)表示引入弹性时间之后工人总代价不能超过未引入弹性时间的工人总代价;式(17)表明至少存在一个工人的预计在线时间超过所需执行时间最长的任务,保证执行时间最长的任务在初次分配时能够有机会被执行。由于考虑工人在线时间为弹性的任务分配问题是组合优化问题,属于NP-hard问题的范畴,不存在时间有效的最优算法,只能考虑次优算法,所以在求解时考虑使用智能算法。相较于其它智能算法,鲸鱼优化算法能够更好地平衡全局寻优和局部寻优阶段且收敛速度更快,因此,在求解式(9)~式(17)所确定的任务分配问题时考虑采用鲸鱼优化算法。
2 求解算法
鲸鱼优化算法[12]是由Mirjalili等提出,其思想源自座头鲸的捕食行为。根据座头鲸的捕食行为将算法分为3个阶段:包围猎物,气泡网攻击,搜索猎物。由于鲸鱼优化算法最初提出是为了求解连续问题,而上述任务分配问题为组合优化问题,因此,需要对鲸鱼优化算法进行改进,使之更加适合求解该任务分配问题。
2.1 改进鲸鱼优化算法
2.1.1 鲸鱼优化算法过程
包围猎物阶段:座头鲸根据猎物的位置更新自身位置,从而接近猎物,称作包围猎物阶段。相关定义如式(18)所示
(18)
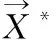
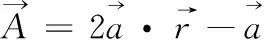
(19)
(20)

气泡网攻击阶段:气泡网攻击阶段座头鲸螺旋移动并吐出气泡以包围猎物。此时,座头鲸的螺旋运动轨迹定义如式(21)所示
(21)
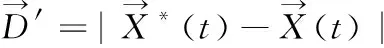
综合上述两个阶段,此时座头鲸处于已经发现猎物并且向猎物移动的过程,因此,这两个阶段也称作局部搜索阶段。通过观察发现,座头鲸在猎物周围游动行为同时包括了包围猎物以及气泡网攻击两种行为。因此,为了描述此时座头鲸的行为,假设座头鲸包围猎物以及气泡网攻击的概率各为50%,此时,座头鲸行为总结如下
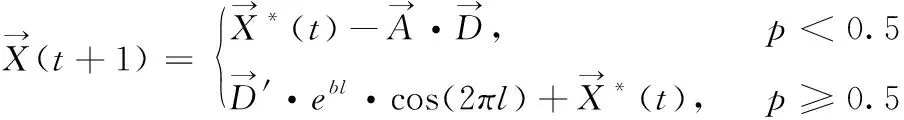
(22)
其中,p为[0,1]之间的随机数。
搜索猎物阶段:在这个阶段,座头鲸还处于寻找猎物阶段,它们根据彼此位置在空间内进行随机搜索。因此,这部分也称作全局搜索阶段,其定义如下
(23)
(24)
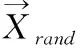
2.1.2 编码及改进
由于鲸鱼优化算法最初提出是为了求解连续优化问题,而工人弹性在线时间的任务分配为组合优化问题,其中涉及到任务和工人的配对问题,因此需要对任务与工人序列进行编码并且对鲸鱼优化算法进行改进,使之能够求解该任务分配问题。
分别将任务和工人编码成两个序列。 [N1,N2,N3,…,Nt] 表示t个任务的排列,其中Ni∈{1,2,3,…,t}; [m1,m2,m3,…,mt] 表示任务对应的执行工人排列,其中mi∈{0,1,2,…,w}。 当mj=0时,表明任务序列中Nj任务未被分配;而当mj≠0时,表示对应位置的任务分配给对应位置的工人,从而确定任务分配结果。对应的任务序列和工人序列相结合为一个鲸鱼,此时,工人总效率即为鲸鱼优化算法的适应度值。在利用鲸鱼优化算法进行组合优化问题求解时,额外设计反转模块与局部搜索模块以保证算法的搜索性能。为更好描述反转模块与局部搜索模块,假设系统中存在9个任务和3个工人。初始化任务序列为[1 2 3 4 5 6 7 8 9],随机生成工人序列为[1 2 3 1 2 3 1 2 1],相同位置的任务和工人构成任务-工人对,表示该任务由该工人执行。
反转模块:如图1所示,选择反转起始点为4,反转长度为4,则需要反转的任务序列为4 5 6 7;反转之后该任务序列变为[1 2 3 7 6 5 4 8 9]。根据优化后的任务及工人序列可以发现任务分配发生了变化。

图1 反转模块
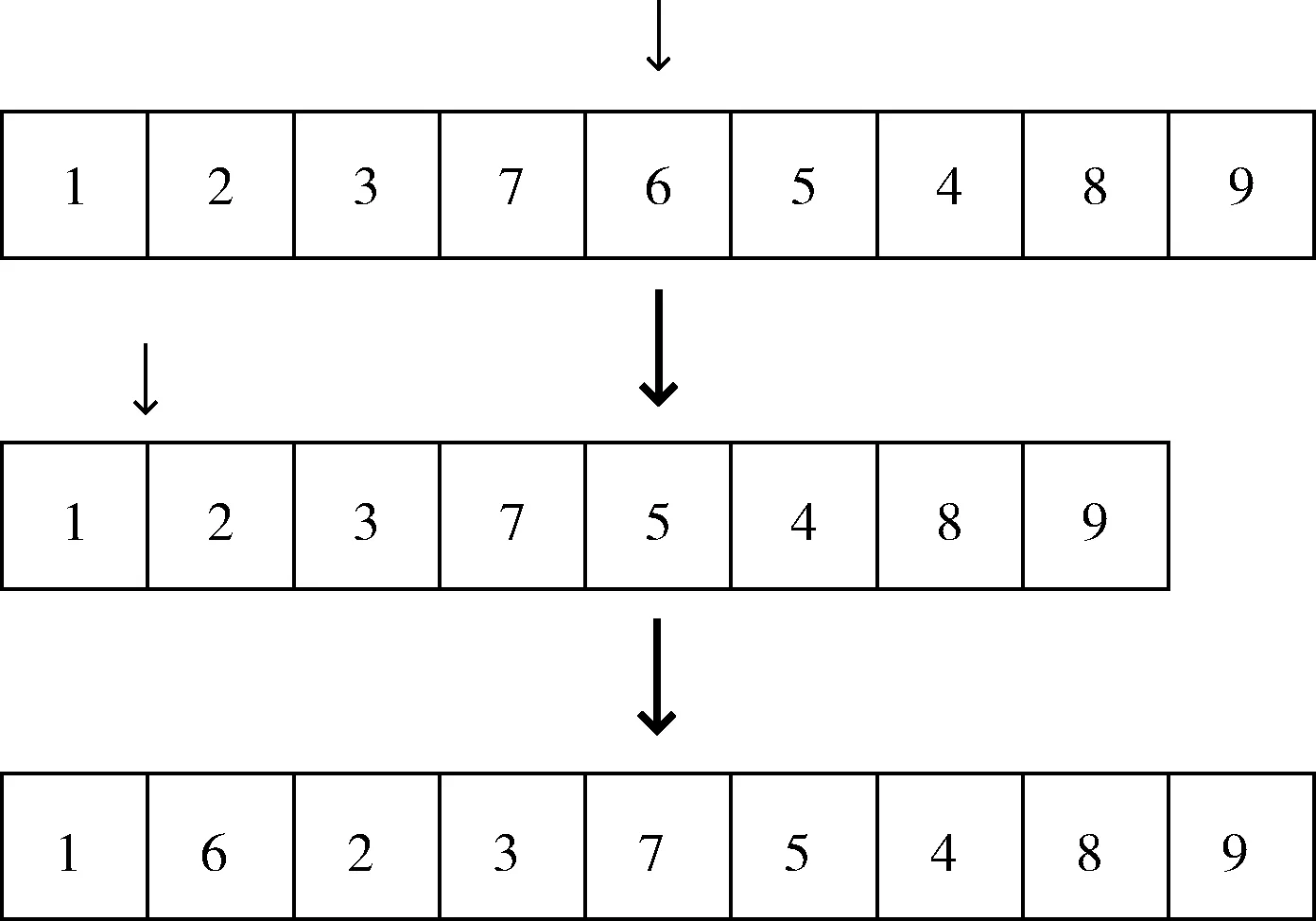
图2 局部搜索模块
局部搜索:如图2所示,选择任务序列中的第5个元素进行局部搜索优化,因此,将第5个元素即任务6剔除,选择第2个位置将该任务重新插入,则该任务序列变为[1 6 2 3 7 5 4 8 9]。结合随机生成的工人序列可知,任务分配发生了变化,使得任务分配的优化结果跳出局部最优。
2.2 两阶段任务分配算法
针对式(9)~式(17)所确定的任务分配模型,设计任务分配过程为两个阶段:初次分配与弹性调整。初次分配阶段中群智感知系统首先将系统中所有任务初步分配给注册工人,系统预评估感知系统所分配任务需花费的总时间,当发现某工人执行完某个任务之后,执行接下来的任务会使工人任务执行时间超过工人预计在线时间,此时,系统确定分配给工人的任务为不超过预计在线时间的部分任务。没有被执行的任务聚集在一起为未分配任务,此时,工人的总代价中都只存在空闲代价,初次分配阶段完成。其过程如算法1所示。
算法1: 初次分配
输入: 工人信息W及任务信息T, 初始化工人任务执行时间MTj’=0(j=1,2,…,w),工人空闲时间ITj’=0 (j=1,2,…,w), 工人总代价TC’=0,单位空闲代价c。
系统将任务随机分配给工人, 生成任务分配集Vj(j=1,2,…,w)
forj=1 towdo
forTvinVjdo
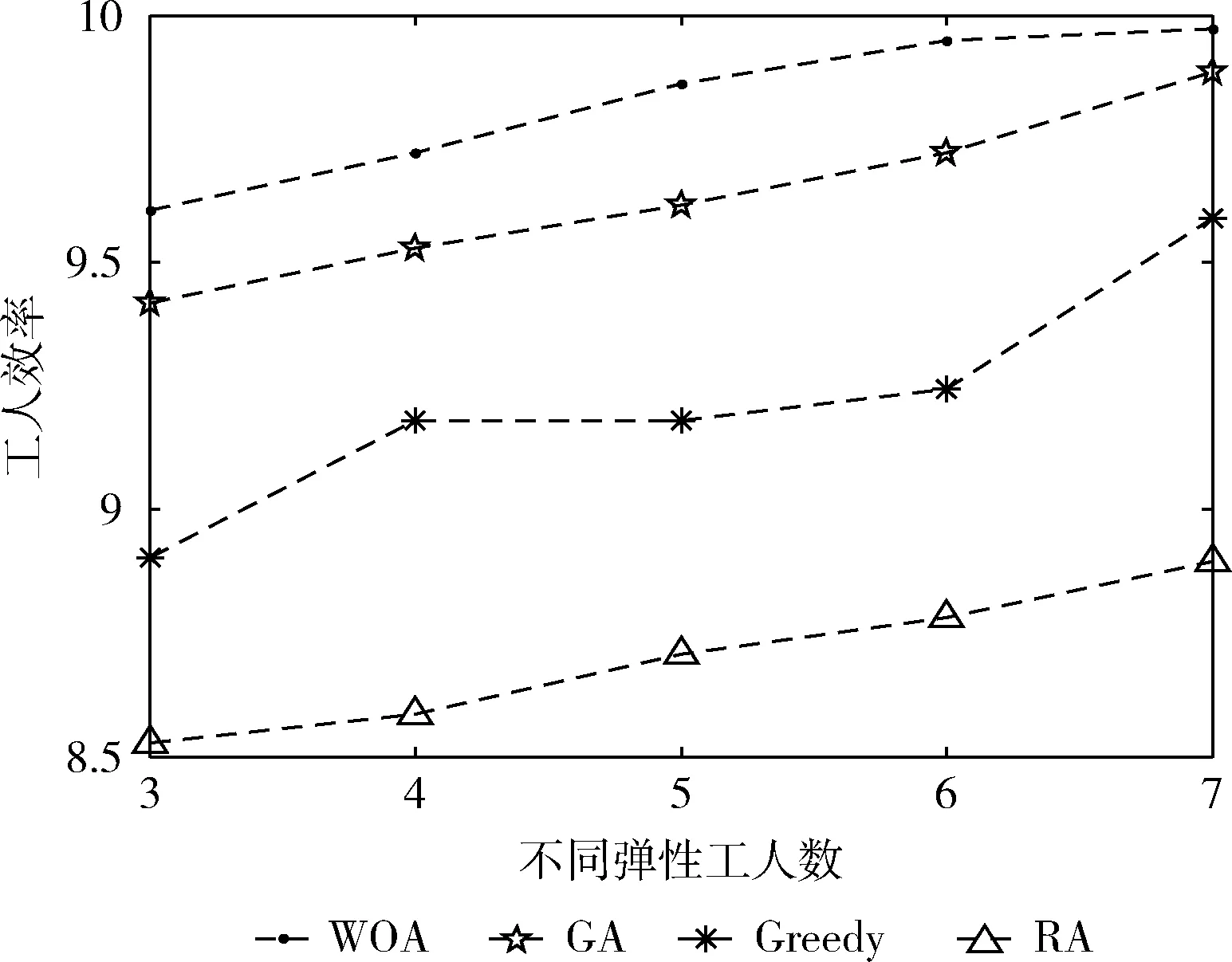
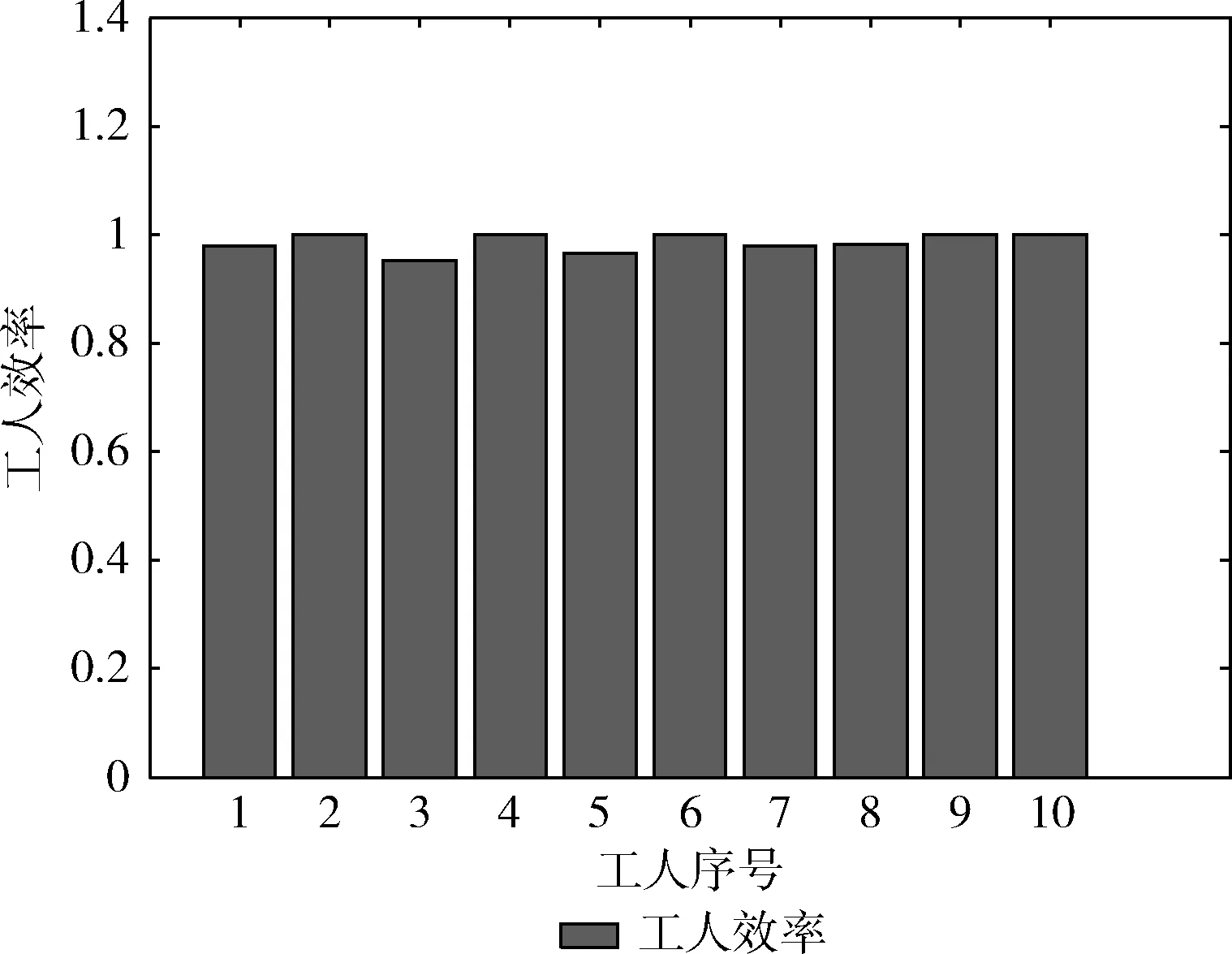
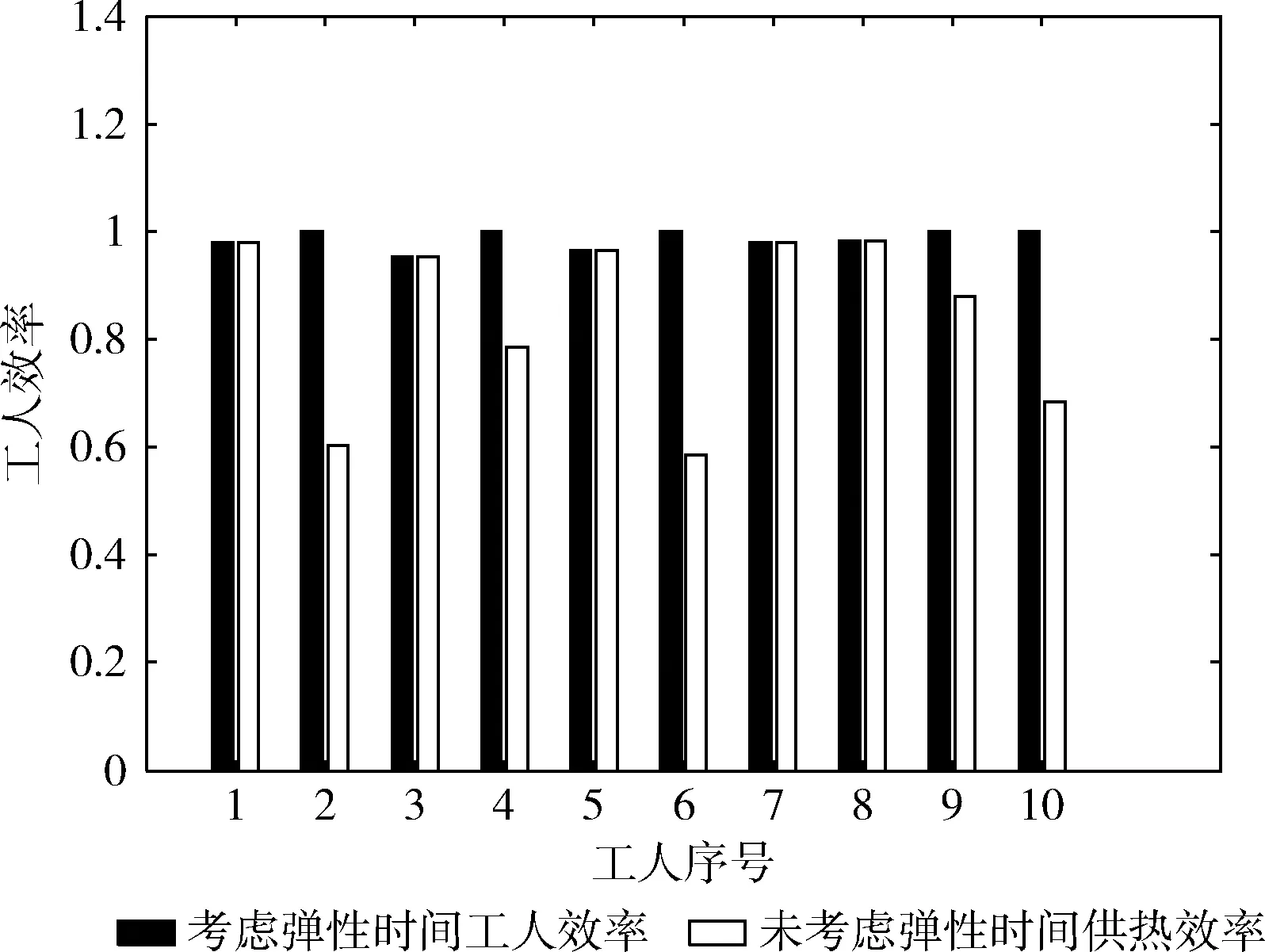
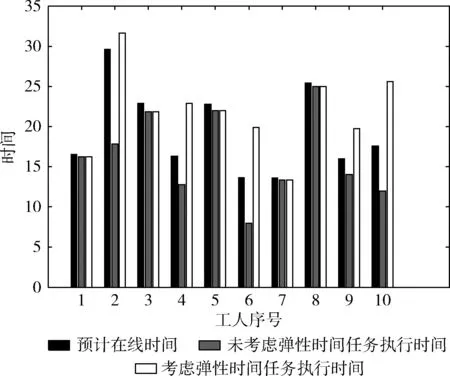
ifMTj’+TTv= MTj’=MTj’+TTv else 将该任务从该工人任务集中转移到未分配任务中 endif endfor ITj’=WTj-MTj’ TC’=TC’+c*ITj’ endfor 输出:工人最终任务集Vj’,未分配任务集V0’,总代价TC。 完成初次分配后,系统开始弹性调整阶段。在弹性调整阶段中,根据每个工人的时间约束可能性以及预设的置信水平,确定工人是否选择延时,从而确定是否为工人分配额外任务。当工人的时间约束可能性大于置信水平时,说明工人任务执行时间不能超过工人预计在线时间,此时工人不选择延长时间;当工人时间约束可能性小于置信水平时,此时工人选择延长时间,执行额外任务,因此将未分配任务集中的某一个任务从未分配任务集中剔除,分配给该工人,在分配该任务时保证任务分配成功后的工人代价不能够超过初次分配时的工人代价。其过程如算法2所示。 算法2: 弹性调整 输入: 任务分配集合Vj’(j=0,1,…,w), 工人时间约束可能性Pbj(j=1,…,w), 预设置信水平z, 初次分配分配阶段工人总代价TC’, 初始化最终工人总代价TC=TC’。 forj=1towdo ifPbj 未分配任务集中选择一个任务预分配分配给工人j 计算TC ifTC’ 将该任务分配给工人j endif endif 更新工人任务集、 未分配任务集 endfor 输出: 最终工人任务集合Vj(j=0,1,…,w), 工人总代价TC。 综合以上两个阶段,在基于鲸鱼优化算法设计的两阶段任务分配算法中,首先执行初次分配,即根据工人、任务的相关信息随机分配任务,然后利用改进鲸鱼优化算法对随机分配结果进行优化;接着执行弹性调整,即根据初次分配结果以及工人时间约束可能性判断工人是否选择延长时间,从而确定是否选择额外任务分配给该工人,经过多次迭代之后得到一个较优的结果。完整的任务分配过程如算法3所示。 算法3: 离散鲸鱼算法 输入: 置信水平z, 工人集W, 任务集T, 工人时间约束可能性Pbj(j=1,2,…,w), 迭代次数maxIter 初始化种群Xi(i=1,2,…,n) 计算工人总效率 X*=工人总效率最高的任务分配方案 Whilet fori=1tondo 更新鲸鱼优化算法中参数a,A,C,l和p 改进鲸鱼优化算法优化初次分配 弹性调整 endfor 计算每个个体适应度值 更新X* t=t+1 endwhile 假设算法的最大迭代次数为T,种群大小为P,工人数量为W。由算法3可知,完整算法中包含初次分配以及弹性调整两个阶段。在初次分配以及弹性调整中,算法的时间复杂度均只与工人数量有关,表示为O(W)。 由于两部分都处于种群迭代优化的内层,因此,算法3的时间复杂度为O(TPW)。 可以看出,算法的时间复杂度是随种群大小、迭代次数以及工人数量线性增长的,这样的复杂度是可以接受的。 通过仿真实验验证所设计任务分配算法的性能,系统参数见表1。由于工人选择延时会执行额外任务,从而得到额外收益,使得工人延时成本降低;而工人空闲时,由于不执行任务而没有额外收益,不能降低空闲成本,因此,设置工人单位延时成本小于单位工人空闲成本。基于表1中的参数设置,我们首先分析置信水平对各算法中选择弹性时间的工人数量的影响。然后,对比分析工人数量变化、置信水平变化以及弹性工人数量变化时,所提任务分配算法与基于遗传算法(genetic algorithm,GA)[13]、贪婪算法(greedy algorithm,Greedy)以及随机分配(random allocation,RA)的任务分配算法的性能比较。其中,基于遗传算法的任务分配算法中,遗传算法被用于优化初步分配结果;基于贪婪算法的任务分配算法中,依次为工人分配使得当前工人总效率达到最大的任务;基于随机的任务分配算法中,根据工人是否选择弹性时间将任务随机分配给工人。最后,验证考虑工人弹性时间相较于不考虑工人弹性时间的优势。本文算法均以MATLAB R2014a为仿真平台,所用机器配置为Intel®CoreTMi7-4710MQ 2.50GHz 8GB RAM,操作系统为Windows。 利用模糊机会约束方法对工人在线时间建模,工人能够根据自身情况选择是否延时以执行额外任务,因此,每次仿真选择弹性时间的工人数可能不同,从而影响优化的结果。在仿真中预设置信水平,随机生成工人的时间约束可能性,当某个工人的该时间约束可能性大于置信水平时,判定该工人不选择弹性时间,当该工人的可能性小于置信水平时,则该工人选择弹性时间,可以看出置信水平的大小会影响到选择弹性时间的工人数,将选择弹性时间的工人称作弹性工人。表2给出了经过重复多次实验后在不同的置信水平下基于鲸鱼优化算法、遗传算法、随机分配以及贪婪算法的任务分配算法中弹性工人数量的平均值。从表2可以看出,随着置信水平的增加,算法中的弹性工人数量也在增加,弹性工人数量在总工人数中所占比例大约等于置信水平。这说明选择弹性时间的工人数量会受到置信水平的影响,当置信水平越大时,能够满足延时要求的工人数量就越多,此时,就有越多的工人选择弹性时间。 表1 参数设置 表2 弹性工人数量随置信水平变化的变化 为了验证置信水平对工人效率的影响,分别取置信水平为 [0.3,0.4,0.5,0.6,0.7] 时进行多次仿真,从而得到图3结果。可以发现在不同的置信水平下,相较于遗传算法、随机分配算法以及贪婪算法,鲸鱼优化算法得到的工人效率最高。此外,在不同算法中工人效率均会随置信水平的增加而增加。 图3 工人效率随置信水平变化而变化 图4给出了工人效率随工人数变化而变化的趋势。可以看出随着工人数量的增加,工人总效率也相应增加,而基于鲸鱼优化算法制定的任务分配算法始终比其它算法所得工人效率好。 图4 工人效率随工人数变化而变化 由于选择弹性时间的工人效率会得到提高,在相同单位代价、工人数量、任务数量以及置信条件下,不同的弹性工人数也会影响到工人总效率,记录在工人、任务数量以及置信水平不变的情况下弹性工人数量分别为3、4、5、6、7时工人总效率的变化。如图5所示,随着弹性工人数的增加,不同算法中的工人的总效率均增加了。鲸鱼优化算法中工人总效率接近最高值,此后,工人总效率增长变缓。此外,随着弹性工人数量增长,基于鲸鱼优化算法制定的任务分配算法的工人效率始终高于其它算法。 图5 工人效率随弹性工人数变化而变化 为了讨论引入工人弹性时间的重要性,图6展示了鲸鱼优化算法的最优任务分配结果中各工人效率。可以看出有一半工人达到了最高效率1;图7展示了工人任务执行时间与预计在线时间的对比,可以看出工人2、4、6、9、10选择了延长时间执行额外任务,所以他们达到了最高效率。因此,考虑工人弹性时间能够提升工人效率。 图6 工人效率 图7 工人执行任务时间与预计在线时间对比 为了进一步展示弹性时间的效果,将考虑弹性时间与未考虑弹性时间的任务分配结果进行对比。从图8中可以看出未考虑弹性时间的工人总效率较低,相比来说,考虑弹性时间的工人效率比不考虑弹性时间的工人效率高,其中工人2、4、6、9、10在考虑弹性时间之后均提高了工人效率。图9展示了工人未考虑弹性时间以及考虑弹性时间之后工人任务执行时间与工人预计在线时间的对比。可以看出,在未考虑弹性时间时,每个工人的任务执行时间都不会超过工人预计在线时间,工人2、6、10即使空闲时间很多,也不会再执行任务;而在考虑弹性时间之后,一部分工人选择延长在线时间执行额外任务以达到更高的效率。图10给出了未考虑弹性时间与考虑弹性时间后工人代价对比。可以看出,考虑弹性时间时工人代价均不会超过未考虑弹性时间时的工人代价,且总代价大幅度降低。因此,考虑工人弹性在线时间不但增加了工人效率,同时也降低了工人总代价,使得资源利用更为合理。 图8 工人效率对比 图9 任务执行时间与预计在线时间对比 图10 工人代价对比 任务分配问题是群智感知相关研究中的重点。针对该任务分配问题,本文考虑工人在线时间为弹性在线时间,采用模糊机会约束规划方法进行建模。由于该任务分配问题为组合优化问题,不存在时间有效的最优解,因此,基于鲸鱼优化算法设计了两阶段的任务分配算法进行求解。仿真结果表明,所设计的任务分配算法相较于其它算法具有更高的工人效率;此外,相较于工人固定在线时间,在进行任务分配时考虑工人弹性在线时间能够提高工人效率同时降低工人成本。2.3 算法的计算复杂性
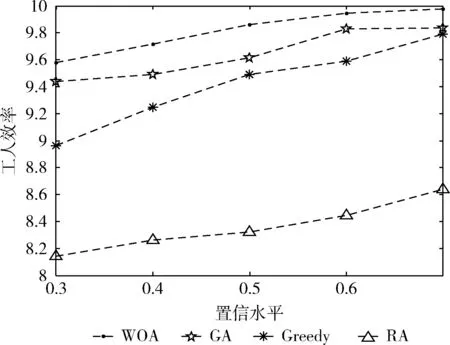
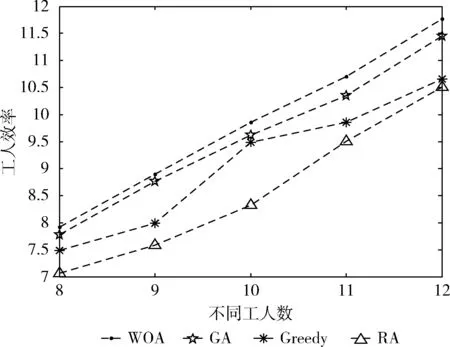
3 仿真结果与分析




4 结束语

