基于分布式存储的OHitchhiker码
李 慧,李贵洋,胡金平,周 悦,江小玉,韩鸿宇
(四川师范大学 计算机科学学院,四川 成都 610101)
0 引 言
作为云计算基础的大规模分布式容错存储系统[1,2],采用纠删码作为数据冗余技术能比多副本技术以更低的存储开销获得相同的数据可靠性。例如Google文件系统[3]部署RS(9,6)码、Baidu Atlas云平台[4]部署RS(12,8)码、Facebook 存储系统[5]部署RS(14,10)码,Hadoop分布式文件系统[6]则提供多种参数的RS (n,k) 码,以供用户选择。在分布式存储系统中,节点失效是一种常态。比如在Facebook的3000个节点生产集群中,每天发生高达20个或更多节点故障[7,8],从而触发修复作业,导致修复带宽占比高达10%-20%。过高的修复带宽使得纠删码技术在实际中的应用受到限制,所以如何降低修复带宽问题成为纠删码的研究热点之一[9,10]。
Reed-Solomon码[11]常常是分布式存储系统的标准设计选择,但是其高昂的修复成本被认为是高存储效率和高可靠性不可避免的代价。为降低修复成本,Rashmi等提出了Piggybacking设计框架,保证在较低的存储开销下,进一步减少修复带宽;Rashmi等对Piggybacking框架进一步完善补充[12]。基于Piggybacking框架,Rashmi等又提出了一种在工程中易于实现的双条带结构Hitchhiker码[13]。Hitchhiker码不仅具有RS码的通用性,同时适用于各种 (n,k) 参数配置,在Facebook存储系统和Hadoop分布式系统中已部署实现。
本文基于Hitchhiker码,提出一种结合不同参数 (n,k) 值动态选择的数据分配算法DSDA(dynamic selection of data allocation algorithm),构造出一种最优分配的OHitchhiker码,可以针对不同 (n,k) 值选择具有最小修复代价的编码结构,进一步降低下载带宽。
1 相关工作
本文定义了如下参数,见表1。

表1 参数
纠删码可通过 (n,k) 两个参数表示,其包含编码、解码两个过程。编码是指通过k个数据块 {A1,…,Ak} 计算产生n个块 {C1,…,Cn}。 解码是指当 {C1,…,Cn} 中不大于n-k个块失效时,则可任选其中k个未失效的块,计算恢复失效块数据。分布式系统中使用的纠删码通常满足两个性质:①最大距离可分性(MDS性质),即能实现所需的容错基础上保证存储冗余也最小;②系统性,即编码后的n个节点中,有k个节点存储原始数据,则r个节点存储校验数据。
通常,我们将n个节点(数据节点和校验节点)统称为一个条带,条带中的节点将会被分到不同的机架(如存储服务器)上去分布式存储。由于数据的分布式存储,导致节点故障频率增高,修复过程也就频繁发生。所谓的修复过程,传统的纠删码在分布式存储系统环境中不是最优的:因为当一个节点失效时,通常会从存储在该节点中的每个子条带中丢失一个块。以RS码和Hitchhiker码为例进行分析,Hitchhiker码编码思想:在双条带RS码上利用异或操作将第一子条带原始数据块 {a1,…,ak} 附加在第二子条带的校验数据块上,以此减少修复成本。Hitchhiker码主要采用均分的数据分配思想。由于数据分配算法的不同,Hitchhiker码可细分为两种:Hitchhiker-XOR码和Hitchhiker-XOR+码。

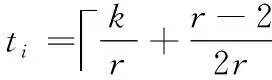
当一个系统节点Nodei失效时,3种码的修复下载量:双条带RS码需要下载2k个数据块;当Nodei中ai∈Sj,(i=1,…,k),(j=1,…,r-1), Hitchhiker-XOR码和Hitchhiker-XOR+码都需要下载k+|Sr| 个数据块;当Nodei中ai∈Sr时,Hitchhiker-XOR+码则需要下载k+|Sr|+r-2个数据块。
以参数 (n,k)=(13,10) 为例,当节点Node8失效时,此时RS码、Hitchhiker-XOR和Hitchhiker-XOR+码的修复下载情况,如图1所示。
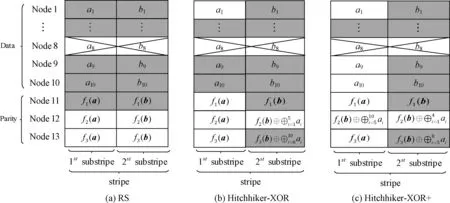
图1 (n,k)=(13,10) 3种纠删码
从图1中可以发现,Hitchhiker-XOR码将原数据块 {a1,…,a10} 均分成2份,其分块情况S={5,5}, 其中S1={a1,…,a5},S2={a6,…,a10}, Hitchhiker-XOR+码则分成3份,分块情况S={4,4,2}, 其中S1={a1,a2,a3,a4},S2={a5,a6,a7,a8},S3={a9,a10}。 由于不同的编码结构,系统节点修复带宽存在差异。
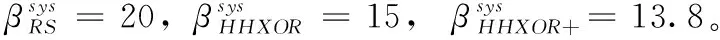
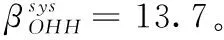
2 OHitchhiker码
本文提出一种最优分配的OHitchhiker编码,通过在编码的分配环节引入一种高效的动态算法,使得OHitchhiker编码可以针对不同 (n,k) 值选择具有最小修复代价的编码结构。
2.1 动态选择的数据分配算法
根据数学推理和OHitchhiker码的特征,本文提出了动态选择的数据分配算法DSDA(dynamic selection of data allocation algorithm)。DSDA执行两步分配:均分分配和移动分配。
为了更好地描述根据不同(n,k)值来动态选择最优的分配,现引入两个参数q和p, 其中q表示商,即q=k/r;p表示余数,即p=k%r。
均分分配:将原始数据块 {a1,…,ak} 划分成r份,每一份存放的数据块数为ti=q,(i=1,…,r); 当k不能整除r时,将余下数据块存放到第r份中,即tr=q+p。 分块情况S={|S1|,…,|Sr|}; 其中 |Si|=ti,(i=1,…,r-1),|Sr|=tr。 此时系统节点数据aj和bj,(j=1,…,k) 的修复下载量为
(1)
此时系统节点的平均修复数据下载量为
(2)
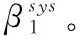
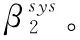
将两者的平均修复数据下载量相减,得到
(3)
当Δβsys>0时,即表示移动后的下载量更少,则需要移动分配,进一步降低修复成本。
移动分配:即当Δβsys>0时,则需要将Sr中的数据移动一块到Si,(i=1,…,r-1) 中,再更新p=p-1, 循环m次移动后,直到Δβsys>0不满足为止。最后得到分块情况S={|S1|,…,|Sr|}; 其中|Si|=q+1, |Sj|=q, |Sr|=q+p-m,(i=1,…,m;j=m+1,…,r-1)。
根据以上原则,动态选择数据分配算法DSDA的过程如算法1所示:①初始分块,得到平均分块数q和剩余分块数p;②均分分配,将原数据 {a1,…,ak} 划分成r份;③移动分配,当Δβsys>0时,将Sr中的数据移一块到Sj,(j=1,…,r-1) 中,更新p, 循环直到Δβsys≤0; ④分配结束,输出分块情况S。
算法1: 动态选择的数据分配算法DSDA
输入:k—数据节点
r—校验节点数
输出:
S—数据分配情况
过程:
步骤1 初始分块:
q=k/r,p=k%r
步骤2 均分分配:
Foriin len (S)
Si←q
IFq>0 Then
Sr←q+p
步骤3 移动分配:
While Δβsys>0
Si←Sr,q--
步骤4 结束, 输出S。
动态选择数据分配算法DSDA紧密契合了OHitchhiker码的双条带结构特性,使得OHitchhiker码在修复过程中首先实现全局均分分配,大幅度降低修复带宽;然后通过不同 (n,k) 参数判断执行移动分配,达到最优动态选择模式,从而降低修复时所需的总数据下载量,保证系统节点的平均修复带宽最低。
2.2 OHitchhiker编码结构
OHitchhiker码继承Hitchhiker码的双条带结构,利用异或操作将数据节点块叠加在校验节点上的方式,根据动态选择的数据分配算法,将系统节点的修复成本降到最低。
OHitchhiker编码过程分成如下3步:
(1)利用RS编码,将原始k个数据 {a1,…,ak} 进行编码,计算产生r个校验块;然后将数据块和校验块,共n个块 {a1,…,ak,f1(a),…fr(a)} 分布式存储在n个节点中,即为一个条带;
(2)根据DSDA分配算法,首先均分分配,将原始数据块 {a1,…,ak} 划分成r份;然后根据式(3)判断Δβsys, 当Δβsys>0时,进行移动分配;得到分块情况S={|S1|,…,|Sr|}; 其中 |Si|=q+1,|Sj|=q, |Sr|=q+p-m,(i=1,…,m;j=m+1,…,r-1);
(3)利用RS编码生成两个条带拼接合成一个条带,细分为第一子条带 {a1,…,ak,f1(a),…fr(a)} 和第二子条带 {b1,…,bk,f1(b),…fr(b)}。 通过将第一子条带的系统节点数据 {a1,…,ak} 分块叠加在第二子条带的校验节点上 {f2(b),…fr(b)}。 为保证MDS性质,第一个校验节点中的数据不作修改。首先利用第一子条带的数据分块情况S, 将前r-1份数据Si,(i=1,…,r-1) 与第二子条带中的后r-1 个校验节点数据进行异或操作,更新保存到校验节点中。然后将第r份数据Sr通过横向减法原则间接保存在第一子条带中的第二个校验节点中,即第一子条带的第二个校验节点的数据减去同一节点的第二子条带数据。
以OHitchhiker码 (n=13,k=10) 为例,编码结构如图2所示。
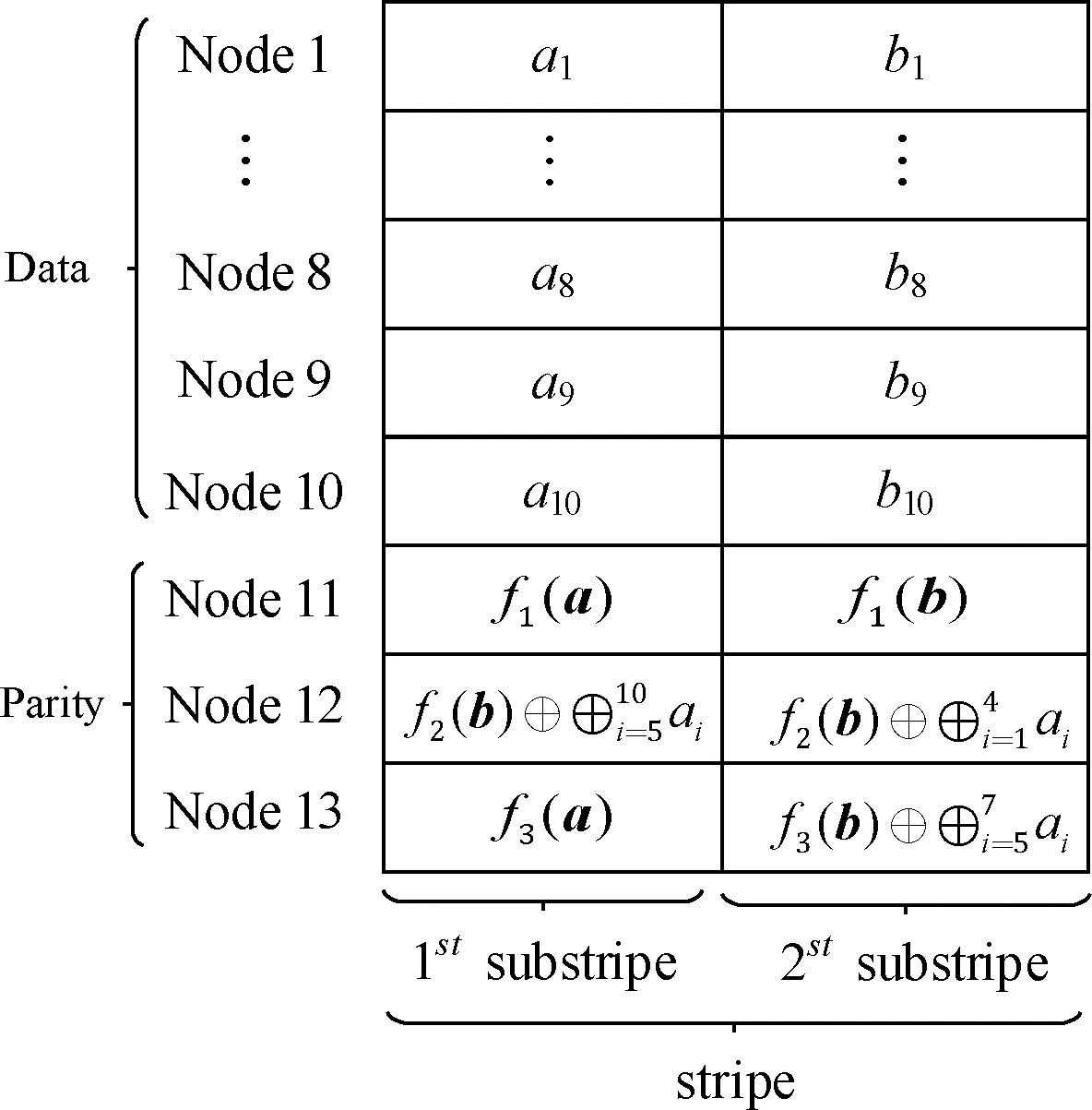
图2 OHitchhiker码 (n=13,k=10) 的编码结构
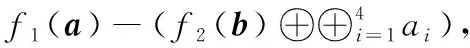
2.3 OHitchhiker修复过程
当节点失效时,通过下载一定数据块,利用MDS性质计算恢复出节点数据,将失效的块重新写入,这个过程被称为数据修复。OHitchhiker码最多能容忍r个节点失效,而在分布式存储系统中单节点失效占比高达90%,所以本文主要讨论单节点失效而启动修复的过程。
OHitchhiker码的修复过程分成如下4步:假设节点Nodei失效,即数据ai,bi失效。
(1)下载第二子条带中的数据{b1,…,bk,f1(b)}/bi, 共k个数据,据MDS性质,计算恢复出原数据bi。
(2)通过动态选择数据分配算法DSDA生成分块情况S, 判断节点Nodei中ai属于Sj,(j=1,…,r-1) 还是Sr。
(3)如果数据ai∈Sj,(j=1,…,r-1), 即存放在第二个子条带的校验节点中。那么首先下载含有数据ai的校验块 [f2(b)⊕Sj], 因为此时b已经全都下载,那么线性组合f2(b) 也就得到;再下载{Sj}/ai, 共|Sj|-1个数据,相互异或恢复出数据ai; 此时共下载 |Sj| 个数据。
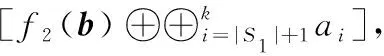
以OHitchhiker码 (n=13,k=10) 为例,当节点Node8失效时,修复过程如图3所示。
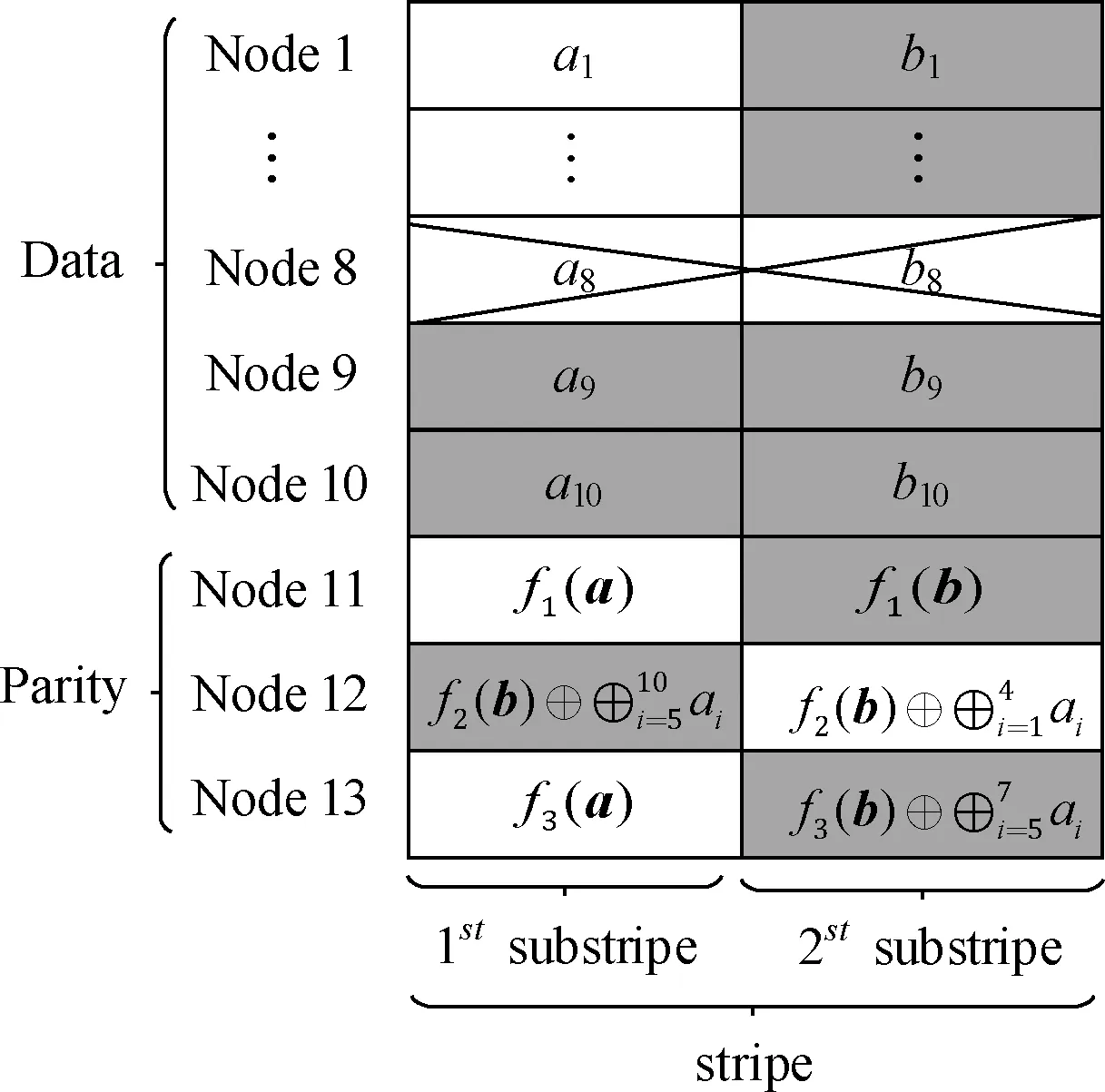
图3 OHitchhiker码 (n=13,k=10) 的节点修复

3 实验结果与分析
本文在HDFS-RAID[14]中实现OHitchhiker码,通过插件方式将编码加入HDFS中,此时的分布式容错存储系统称为HDFS-OHitchhiker。根据实验结果,对比分析OHitchhiker码与RS码、Hitchhiker-XOR码和Hitchhiker-XOR+码的平均修复带宽、修复带宽率和总修复下载量。
3.1 实验环境
实验通过部署分布式系统集群,集群由一个NameNode节点和19个DateNode节点组成。所有节点运行在Ubuntu16.04系统和JDK1.7.0_37中,其中每个节点配置两个8核Intel 2.5 GHz处理器,48 G RAM,2T硬盘和 2 GB/s 以太网卡。
实验数据为500个640M文件,保持默认HDFS的数据块大小64 M,通过设置不同 (n,k) 参数和4种编码策略(OHitchhiker码、RS码、Hitchhiker-XOR码和Hitchhiker-XOR+码),将每个文件分块编码分布式存储在DataNode节点中。
3.2 实验分析
3.2.1 平均修复带宽
为了更全面的比较,我们通过实验计算并对比了满足k∈{1,…,100},n∈{k+1,…,2k} 的所有取值下4种编码的实际平均修复带宽,发现OHitchhiker码在所有 (n,k) 参数情况下都是最优的。
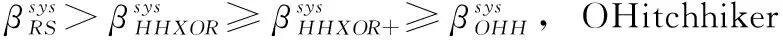
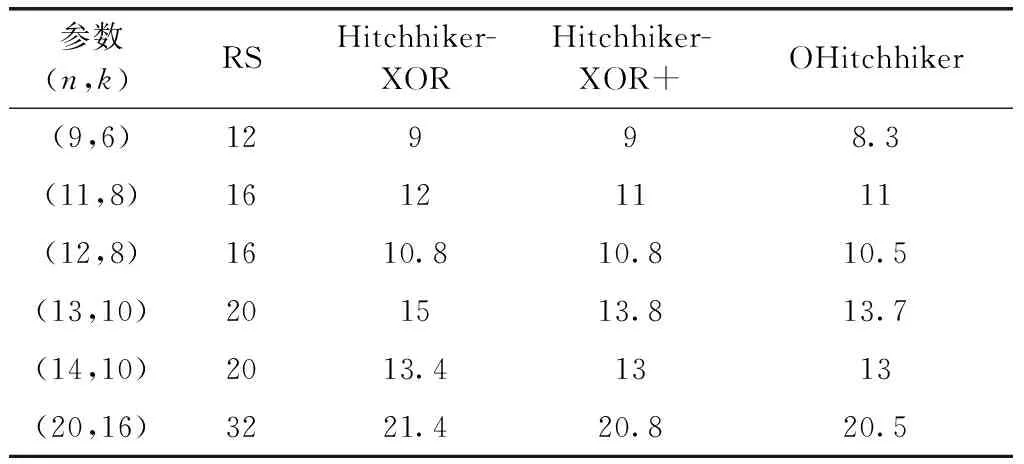
表2 系统节点平均修复带宽对比
3.2.2 修复带宽率
当系统节点失效时,修复节点下载量占原数据总量的百分比,称为修复带宽率rsys
(4)
图4描述在 (n,k)={(8,5),(9,6),(12,8)} 这3种取值下,Hitchhiker-XOR,Hitchhiker-XOR+和OHitchhiker码之间的系统节点修复率对比图,图中的横坐标表示参数 (n,k), 纵坐标表示系统节点的修复带宽率。
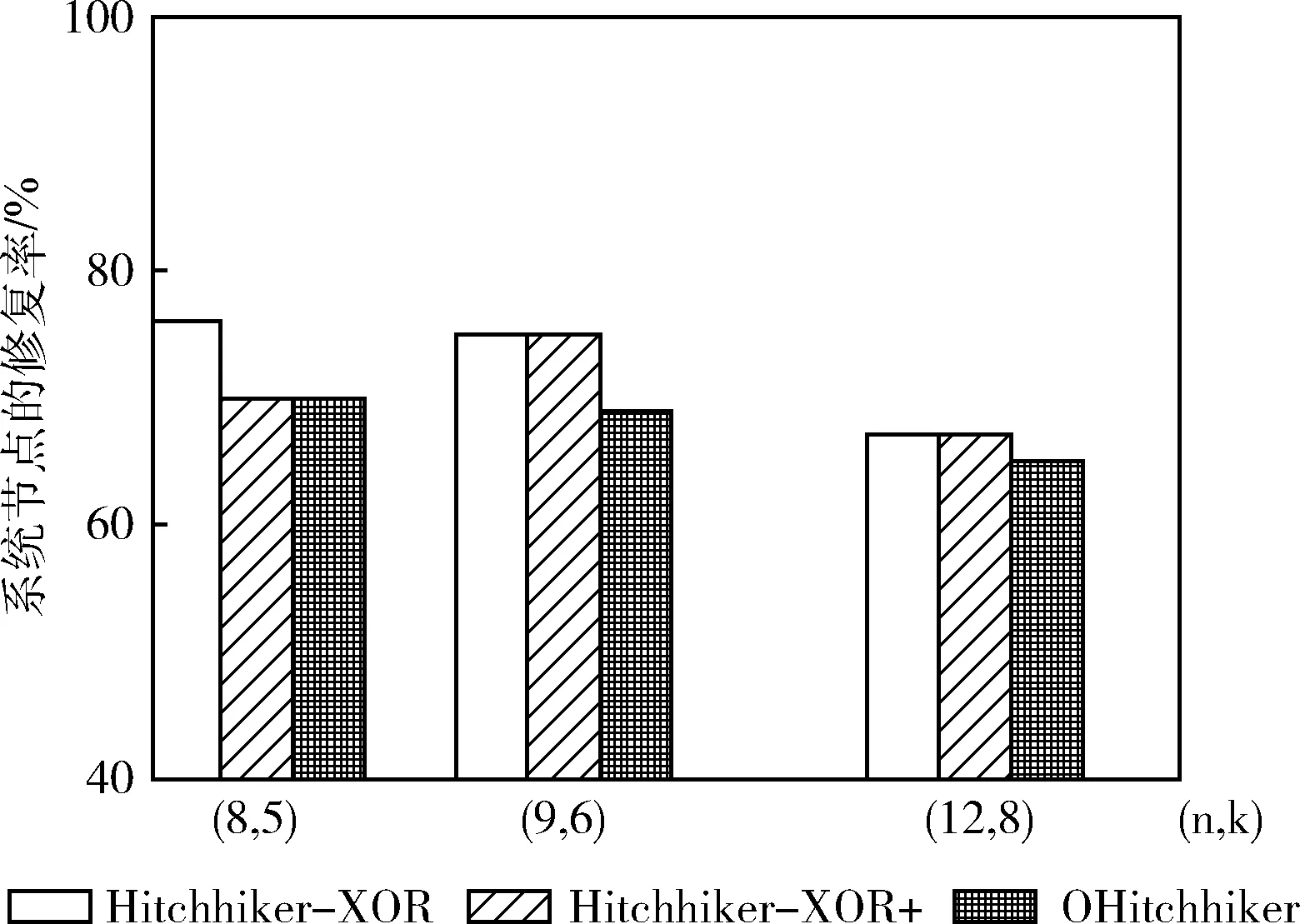
图4 Hitchhiker和OHitchhiker码的修复率对比
从图4中可以发现,OHitchhiker码的系统节点修复率始终保持最低。在参数为 (n,k)=(8,5) 时,OHitchhiker码的修复带宽率相比于Hitchhiker-XOR码降低了6%,与Hitchhiker-XOR码则相同。在参数为 (n,k)=(9,6) 时,OHitchhiker码的修复带宽率相比于Hitchhiker-XOR码和Hitchhiker-XOR+码都降低了5.6%。在参数为 (n,k)=(12,8) 时,OHitchhiker码的修复带宽率相比于Hitchhiker-XOR和Hitchhiker-XOR+码都降低1.6%。
3.2.3 总修复下载量
修复每个系统节点所需的下载量之和,称为总修复下载量δsys
(5)
图5(a)描述在保持总节点数 (n=12) 不变的情况下,随着校验节点数 (r=1,…,6) 增加,RS码、Hitchhi-ker-XOR码、Hitchhiker-XOR+码和OHitchhiker码之间的下载量对比折线图。图中横坐标表示校验节点数,纵坐标表示系统节点总修复下载量。
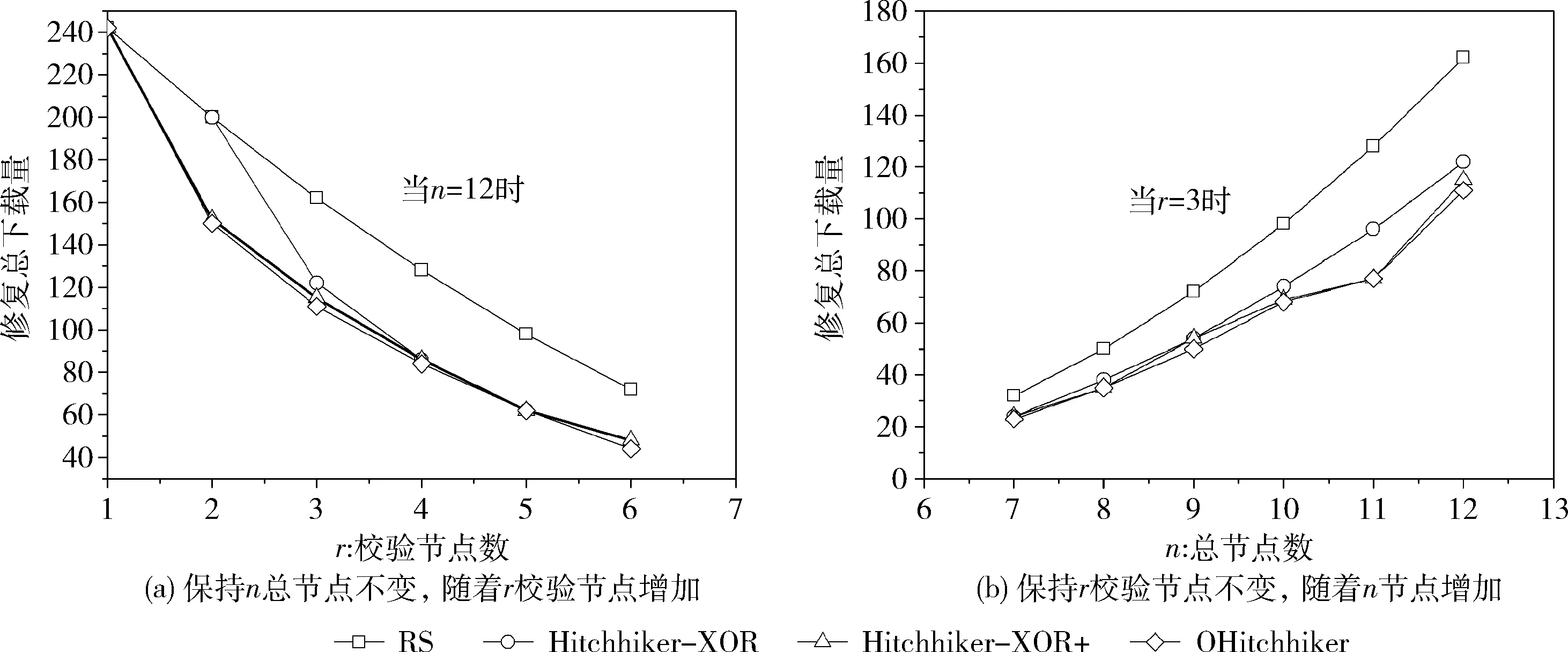
图5 RS、Hitchhiker和OHitchhiker码的总修复下载量对比
图5(b)描述在保持校验节点数 (r=3) 不变的情况下,随着总节点数 (n=7,…,12) 增加,RS码、Hitchhiker-XOR码、Hitchhiker-XOR+码和OHitchhiker码之间的下载量对比折线图。图中横坐标表示总节点数,纵坐标表示系统节点总修复下载量。
从图5中可发现,随着r的增加,RS码、Hitchhiker-XOR码、Hitchhiker-XOR+码和OHitchhiker码的修复下载量整体减少;随着n的增加,RS码、Hitchhiker-XOR码、Hitchhiker-XOR+码和OHitchhiker码的修复下载量整体增加。所以不管是总节点还是校验节点怎样变化,相比于RS码、Hitchhiker-XOR码和Hitchhiker-XOR+码,OHitchhiker码的总修复下载量始终保持最低。
4 结束语
本文通过研究分布式存储系统的Hitchhiker码,在分析均分数据分配算法的基础上,提出一种最优分配的OHitchhiker码。它可针对不同 (n,k) 值动态选择最优的数据分配算法,利用DSDA算法使得编码结构具有最小修复带宽,进一步降低修复成本。理论分析及实验结果表明,在任意 (n,k) 参数取值下,对比RS码和Hitchhiker码,OHitchhiker码始终保持最低修复下载带宽。
但是本文基于Pigyybacking框架下设计的OHitchhiker码,只降低了系统节点失效时的修复下载带宽;当校验节点失效时,仍根据MDS性质下载任意k个数据进行修复,没有进行任何改进。下一步工作将关注校验节点的修复过程,进一步减少校验节点的修复下载带宽。

