逼近插值于一体的二次Bézier曲线同次扩展

程黄和

（汕头职业技术学院 自然科学系，广东 汕头 515078）

用Bernstein基函数定义的Bézier曲线曲面［1-2］是计算机辅助几何设计（CAGD）中一个经典的造型工具，它具有许多优良的性质，在实际的工程中也得到了广泛应用.然而，Bézier曲线曲面也存在不足，如给定控制顶点后，Bézier曲线曲面的形状是唯一的，如果要调整曲线曲面的形状，就必须修改控制顶点，而且Bézier曲线只具有插值作为端点的控制顶点，对其他控制顶点不具有插值的特性，但插值曲线也是CAGD的主要研究对象.为了克服上述不足，学者们研究诸多带形状参数的Bézier曲线曲面［3-9］，通过引入形状参数，使新的Bézier曲线曲面具有更加灵活的形状可调性.但现有带形状参数的n 次Bézier 曲线曲面，多是由一组n+1 次多项式基函数来定义的，也就是说扩展了的n 次Bézier 曲线，虽然引入了可调整曲线形状的参数，但提高了基函数的次数，且所定义的带形状参数的n次Bézier曲线曲面只具有类似Bézier曲线曲面逼近控制顶点的性质，而不可插值控制顶点.

本文给出了二次Bézier曲线的一种同次扩展，在不改变Bézier曲线基函数次数的情况下，引入一个形状参数，使得曲线有更多的自由度，更加的灵活调整曲线形状，特别地，当形状参数λ=-1 时，所生成的曲线具有插值所有控制顶点的特性，能更好地满足实际应用中不同的需求.

1 二次λ-Bernstein 基函数及其性质

首先给出带形状参数的二次λ-Bernstein 基函数，再讨论其性质.

定义1：对∀t ∈[0,1],0 ≤λ ≤1,称关于t的多项式

为带形状参数λ 的二次λ-Bernstein 基函数.

二次λ-Bernstein 基函数（1）具有下列性质

性质1 当λ ∈[0,1),二次λ-Bernstein 基函数b0,2(λ,t),b1,2(λ,t),b2,2(λ,t)是线性无关性的.

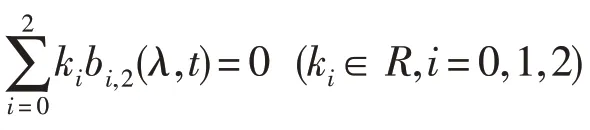
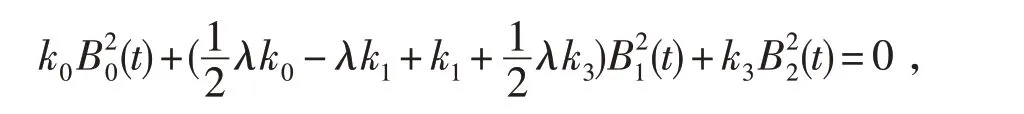
性质3 非负性.即对∀t ∈[0,1],0 ≤λ ≤1,有bi,2(λ,t)≥0(i=0,1,2);特别地当λ=0 时

此时二次λ-Bernstein 基函数为二次Berstein基函数.

当λ=1时

当λ=-1时

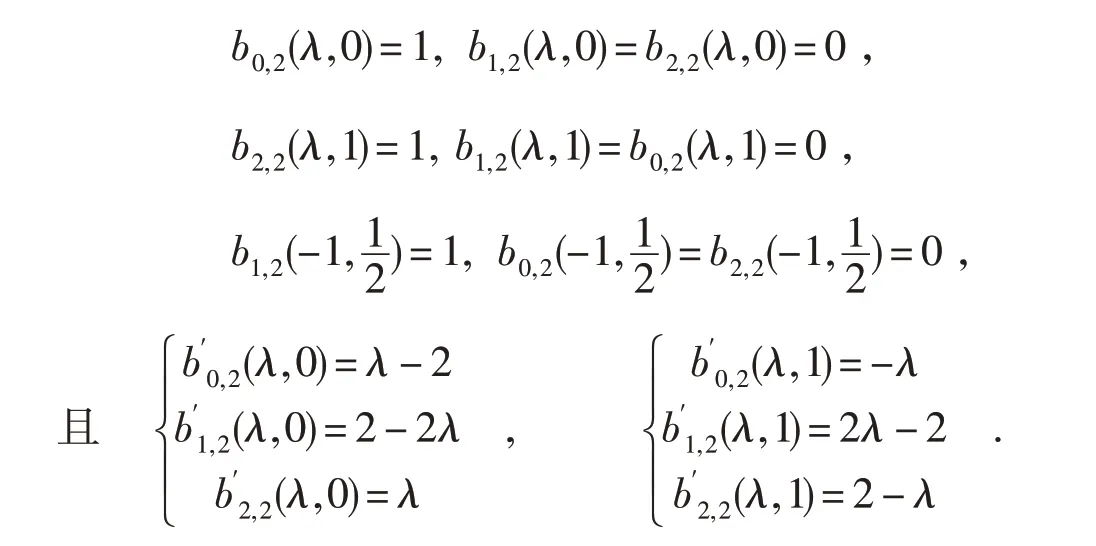
性质5 对称性.b0,2(λ,t)=b2,2(λ,1-t)，b1,2(λ,t)=b1,2(λ,1-t).

2 带形状参数的二次Bézier曲线

本节给出带形状参数的二次Bézier曲线的定义及其性质.

定义2 给定控制顶点Pi∈Rd(d=2,3;i=0,1,...2n)和节点u0＜u1＜…＜un，对∀u ∈[ui-1,ui],

i=1,2,…n,定义多项式曲线段

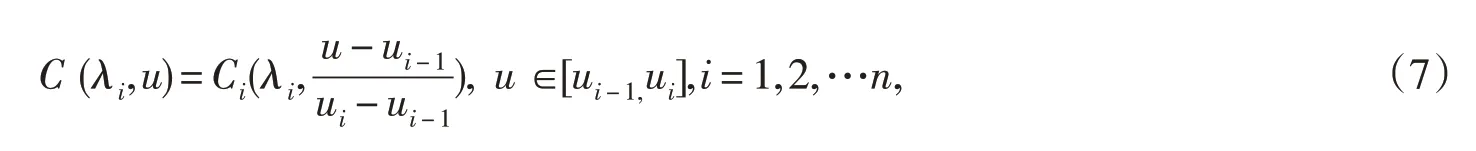
则曲线C (λi,u)(i=1,2,…n)是定义在[u1,un]上的分段多项式曲线，是二次Bézier曲线的推广.通过改变形状参数λi(i=1,2,…n)可以改变曲线的形状.

性质6 式（6）所定义的曲线段首末端点及导矢

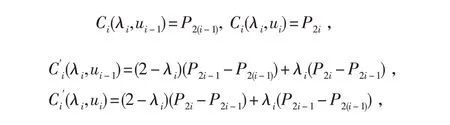
即该曲线段插值首末端点，但仅当λi=0(i=1,2,…n)时才与控制多边形的首边和末边相切.

性质7 由λ-Bernstein 基函数的性质3 知，当λi=-1(i=1,2,…n)时，曲线段Ci(λi,t)不仅过首末端点P2(i-1),P2i，且过控制点P2i-1.此时曲线C (λi,u)(i=1,2,…n)由若干插值曲线段组成.

由二次λ-Bernstein 基函数的性质，容易得到式（6）所定义的曲线还具有对称性、凸包性和几何不变性.

3 曲线的应用

图3-1给出了形状参数λ 取不同值得二次λ-B 基的图像.从图3-1可以看出当λ(0 ≤λ ≤1)值较小时，3个二次λ-B 基图像的切线斜率变化较大，因此当λ(0 ≤λ ≤1)值较小时，本文所定义的带形状参数的二次Bézier曲线更靠近控制多边形.

图3-2给出了具有相同控制顶点，但形状参数λ 取不同值的带形状参数的二次Bézier曲线.图3-2中虚线为控制多边形，实线部分依次为λ=2,1,0.5,0,-0.5,-1,2 时带形状参数的二次Bézier 曲线.可见，当0 ≤λ ≤1 时，曲线位于控制多边形内，且λ 越小，曲线越靠近控制多边形；当λ =-1 时，曲线为过3各控制顶点的插值多项式曲线，λ =1 时，曲线为连接首末端点的线段，且这些性质具有一般性.

图3-3和图3-4给出了λ =0.5,0.3,0,-1时的星形花瓣、六角形花瓣的应用实例.

本文所定义的带形状参数λ 的二次Bézier 曲线，当0 ≤λ ≤1 时，所生成的曲线位于二次Bézier曲线与连接控制顶点首末端点的线段之间，随着形状参数λ 的改变，可以调整曲线的形状，当λ=-1时，所生成的曲线为插值控制顶点的二次多项式曲线.后续将进一步讨论用（2）式定义一般的带形状参数的n次Bézier曲线，并讨论其性质.

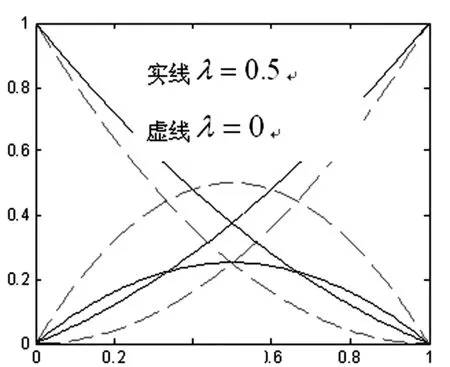
图3-1

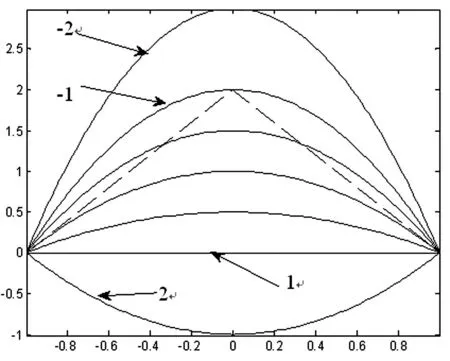
图3-2

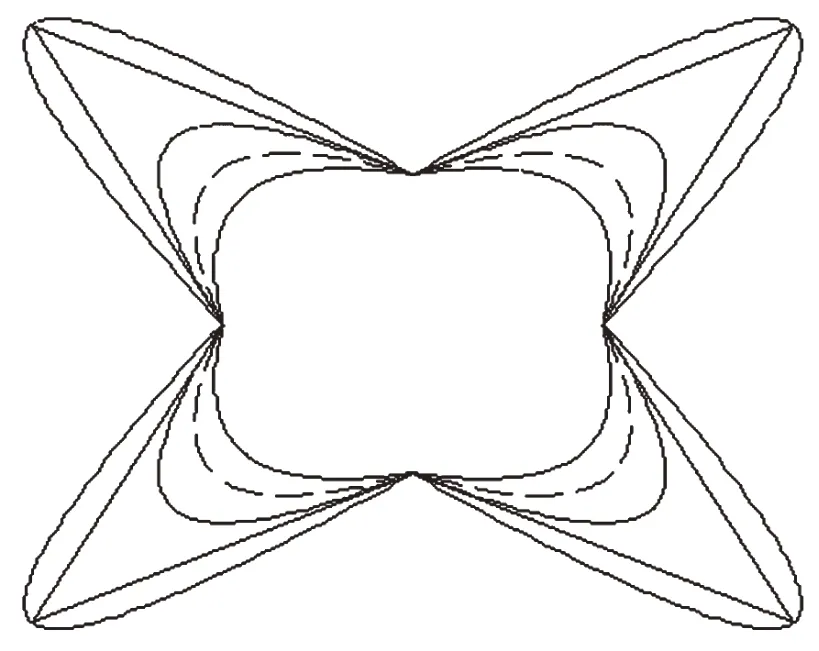
图3-3 λ=0.5,0.3,-1

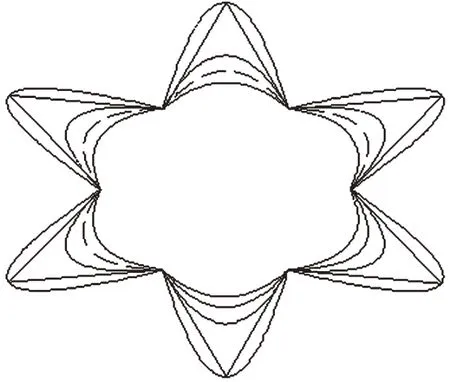
图3-4 λ=0.5,0.3,0,-1