无码间串扰基带传输系统的仿真设计

汤巧治,陈双燕

（闽南理工学院电子与电气工程学院,福建泉州 362700）

由于各种噪声和随机因素的影响，进行通信系统实际电路及性能的试验与研究已经变得不可行。若系统若干参数不满足工程要求，意味着整个通信系统需要重新建设，如此代价实在太大。因此，Matlab作为强大的计算机辅助分析与设计工具，结合其系统仿真方法，人们可以迅速构建一个通信系统模型，提供一个便捷、高效和精确的评估平台。此法将有助于提高新技术理论成果转化为实际产品的效率，进一步降低成本，因而越来越受到业界的青睐[1]。数字基带传输是数字频带通信系统的基础，其研究内容涉及码间串扰（InterSymbol Interference，ISI）的成因以及消除技术、功率谱（power spectral density，PSD）分析和抗噪声性能分析等[2]，因此研究并改善基带传输系统的性能意义重大。

1 基带传输系统原理分析

基带传输系统框图如图1所示。发送滤波器至接收滤波器总的传输特性为H(ω)，则H(ω)=GT(ω)C(ω)GR(ω)。其中，GT(ω)、C(ω)、GR(ω)分别对应发送滤波器、信道和接收滤波器的频谱[2-3]。

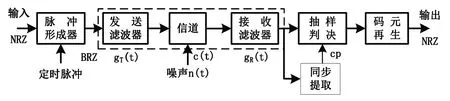
图1 基带传输系统框图

所谓基带传输系统的码间串扰ISI是由于系统传输总特性不理想，导致前后码元的波形畸变、展宽，并使前面波形出现很长的拖尾，蔓延到当前码元的采样时刻上，从而对当前码元的判决造成干扰[4]。相关理论分析表明：奈奎斯特第一准则是判断一个基带系统能否实现无ISI的理论依据。工程上，具有滚升余弦频率特性的传输信道Hrcos(ω)可满足无码间串扰传输要求[1-2]，其频谱为：

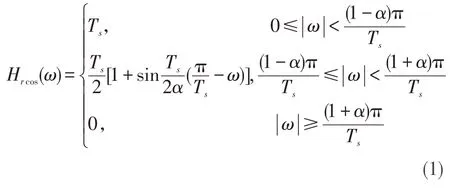
其中，Ts为一个码元的持续时间，0 ≤α≤1称为滚降系数。其冲激响应为：

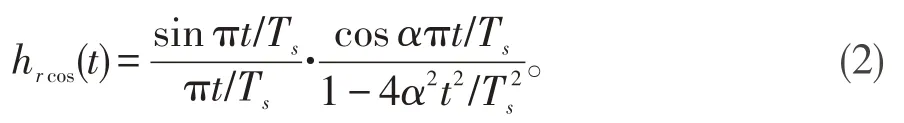
对于物理信道是加性高斯白噪声信道的情况，可以证明，当发送滤波器与接收滤波器相互匹配的时候，即GT(ω)=GR∗(ω)时，通信性能（误码率最小）达到最佳[1]。对于理想的物理信道(C(ω)=1)，收发滤波器相互匹配时有：

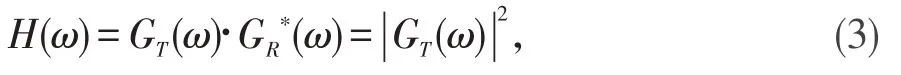
此时可求得发送滤波器和接收滤波器的传递函数的实数解为：

无ISI条件下，信道传递函数是滚升余弦的，匹配的收发滤波器称为平方根滚升余弦滤波器(Square Root Raised Cosine Filter)[1]，其传递函数的实数解为：

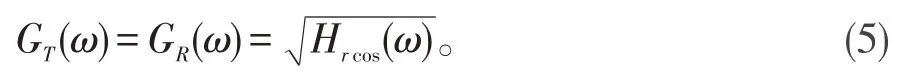
匹配的收发滤波器的冲激响应是：

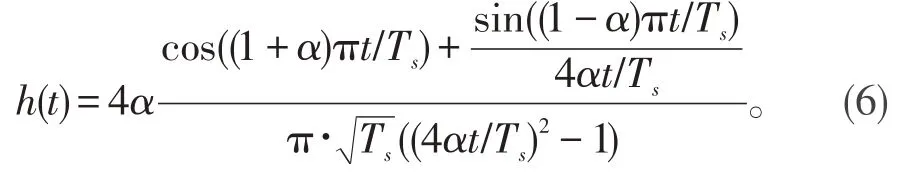
工程上，滚升余弦滤波器和平方根滚升余弦滤波器通常用FIR滤波器来近似实现。Matlab通信工具箱中提供了设计升余弦滤波器的函数“rcosine”，用于计算升余弦或平方根升余弦滤波器的写法为[1]：num=rcosine(Fd,Fs,'fir/normal',r,delay)或者num=rco⁃sine(Fd,Fs,'fir/sqrt',r,delay)。

其中，'fir/normal'用于FIR滚升余弦滤波器设计，'fir/sqrt'用于FIR平方根滚升余弦滤波器设计；r是滚降系数，在0到1之间取值；Fd为输入数字序列的码元速率；Fs为滤波器采样率，其值必须是Fd的正整数倍；delay是滤波器输入到响应峰值之间的时延（单位是码元周期个数）。

2 基带系统仿真设计

基于Matlab/Simulink对数字基带无ISI传输系统进行系统建模，具体模型如图2所示[5]。

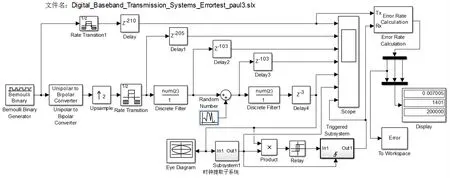
图2 无ISI基带传输系统的Simulink模型（高斯噪声Var=0.01 W）

基带传输系统模型的发送部分各模块说明如下，选用贝努利二进制序列发生器（Bernoulli Bina⁃ry Generator）模块作为系统信号源，来产生单极性非归零矩形脉冲（NRZ），设置信源传码率为1000 Baud（数值上等于比特率1000 bit/s），其输出为冲激脉冲形式的数据序列。单双极性转换模块将NRZ转换成BRZ。系统仿真时，系统的仿真速率设置为10000（即1e4）Hz，对应的固定仿真步长为1e-4 s。因此BRZ数据进入发送滤波器之前需要进行采样率（速率）转换，由上采样和速率转换两个模块实现。发送滤波器为平方根升余弦滤波器，以DSP系统工具箱的“Discrete Filter”模块实现，参数设置如图3。

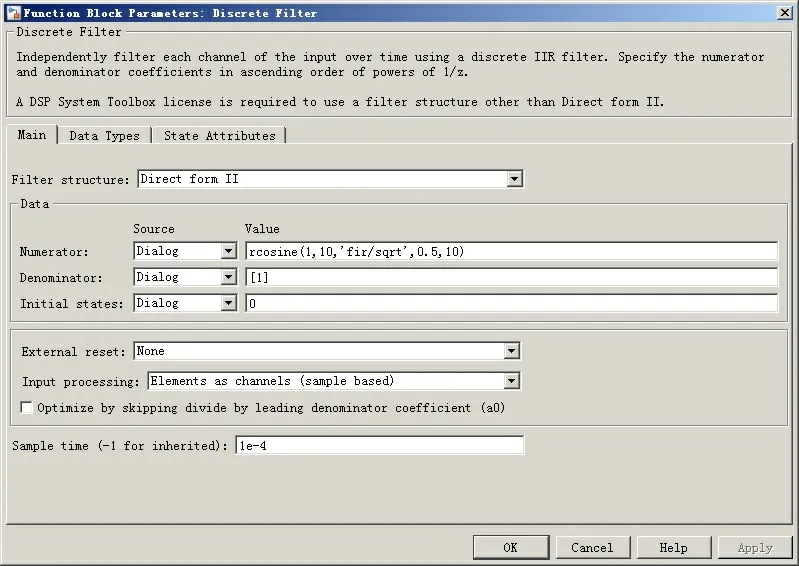
图3 平方根滚升余弦滤波器参数设置

模块关键参数说明如下：分子系数通过“rco⁃sine”函数计算，滚降系数为0.5，滤波器延时为10个码元时间，故设置为：rcosine(1,10,'fir/sqrt',0.5,10)；其分母系数设置为1；采样周期与系统仿真步长一致。信道为加性高斯信道，采用随机数发生器和加法器来实现。随机数发生器产生的高斯噪声均值（Mean）设为0，Var设为固定值0.01 W。由随机过程分析可知，噪声的方差即是噪声平均功率[2]。

接收部分，接收滤波器与发送滤波器相匹配，参数设置与发送滤波器相同。将接收信号进行眼图观察。眼图是一系列数字信号在示波器上累积而显示的图形，因形状像人眼睛而得名。在工程上，为了便于观察接收波形中的码间串扰和噪声的情况，可在采样判决设备的输入端口处以恢复的采样时钟作为同步，用示波器观察该端口的接收波形。Simulink眼图模型参数设置如图4所示。

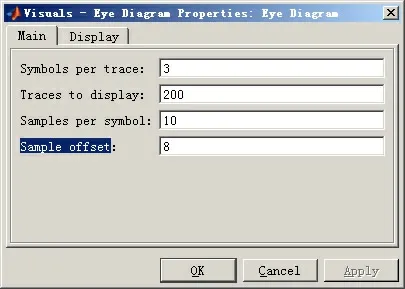
图4 眼图模块参数设置

眼图关键参数设置如下：每次扫描显示（Sym⁃bols per trace）的码元个数若设置为3，则显示3只眼睛；每个码元的采样点数（Samples per symbol）设置为10个；并调整采样延时偏移量（Sample offset），使图位于观察范围的正中央。

接收端采样判决时需要提供位同步时钟脉冲，由时钟提取子系统来恢复，其内部结构如图5所示。

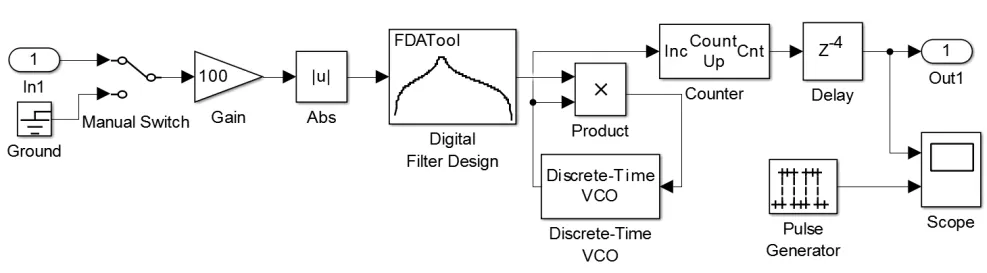
图5 位同步时钟提取子系统

其中，Abs求模模块的作用是倍频。由于信源的传码率为1000 Baud，故IIR带通滤波器的中心频率应为2000 Hz，其通频带设置为1900～2100 Hz。采用锁相环来锁定定时脉冲的二次谐波分量，再通过二分频得出位定时脉冲。故压控振荡器VCO的静态频率可设置为1995 Hz左右，灵敏度8 Hz/V，输出信号幅度为1 V，采样时间同系统仿真步长。计数器最大值设置为1，用于二分频。延时模块用于调整时钟起始时刻对准眼图的最佳采样时刻。

接收端数据恢复部分由乘法器、滞环比较器（Relay）和触发子系统（Triggered Subsystem）构成，分别实现采样、判决以及数据脉冲的再生。由于基带系统传输的双极性信号，所以Relay模块的判决电平设置为0，大于0判为1，否则判为0。触发子系统设置为上升沿触发，用来恢复NRZ矩形脉冲数据。

3 基带传输系统结果测试

3.1 仿真环境说明

本次设计在Matlab 2014b版本的仿真环境中进行。仿真求解器采用固定步长方式，步长为1e-4 s。由于发送滤波器、接收滤波器以及采样判决过程均存在一定的延时，为使示波器各个窗口的信号波形能精确对齐，需要精心设置各部分观测点信号的延时量。各点延时量具体值见图2中5个Delay模块所示。

3.2 基带传输系统测试结果

图2为无ISI基带传输系统模型某次仿真所得结果。现将该次仿真结果补充说明如下：随机数发生器中高斯噪声Var=0.01 W，Matlab仿真时间设置为20 s（200000个仿真步长），所得误码率Pe=0.007005。

（1）功能分析

基带系统模型仿真结果的各观测点信号均已送至示波器进行显示，示波器各信号波形如图6所示。

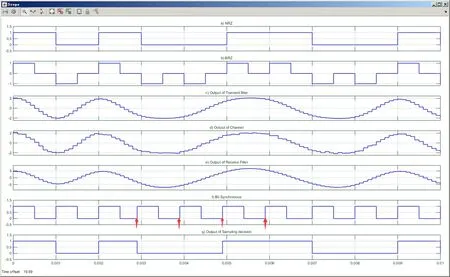
图6 基带传输系统各点信号波形

现对基带传输系统各点信号波形进行分析。示波器设置信号波形显示的时间范围是0～0.01 s。示波器共设置7个显示窗口。第1个波形为系统信号源产生的单极性非归零矩形脉冲（NRZ）。由于码率为1000 Baud，因此一个码元持续时间（码元周期）为0.001 s，所以图6第一个窗口显示的NRZ个数刚好10个，分别表示二进制的1010011001。第2个波形为对应的双极性归零矩形脉冲（BRZ）。第3个波形为经发送滤波器变换后的升余弦信号，滚降系数为0.5。第4个波形为叠加上高斯白噪声后的升余弦信号，即经信道传输的信号。第5个波形为接收滤波器输出信号。第6个波形为位同步时钟信号，对比发送端的BRZ波形，同步保持时间约为6个码元持续时间，有4个时钟同步脉冲出现微小偏差（见图6中红色箭头所示）。当时钟同步出现偏差的值大于一个阈值后，同步提取子系统中的锁相环开始工作以获取同步时钟。第7个波形为经采样判决后恢复的NRZ矩形脉冲。在这一阶段虽然出现微小的时钟偏差，但接收端仍能够正确无误地恢复信源发送的数据。

（2）眼图分析

将接收端经接收滤波器滤波之后的升余弦信号进行眼图观察和分析，所得眼图波形如图7所示。

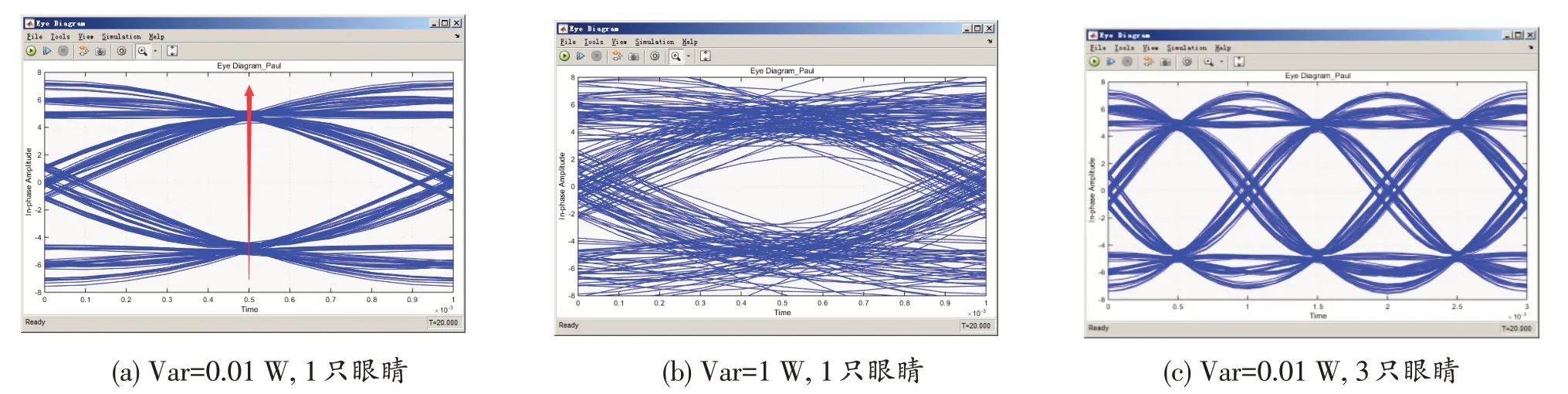
图7 接收信号眼图波形分析

从图7可知，当方差Var=0.01 W时，接收信号的眼图规整，信号线迹清晰。图7(a)中，中央的红色箭头表示该码元的最佳采样判决时刻。当噪声方差增大至1 W时，眼图线迹模糊，此时将导致接收端恢复数据时误码率急剧增大。

（3）误码率分析

误码率是数字通信系统一个极为重要的性能指标。仿真过程中发现，单次启动模型仿真时，不同的仿真时间会得出差别较大的误码率值，这是由Matlab仿真环境本身的影响导致的。每一次仿真结果需要满足一定的数据点数才能得出较为精确、可靠的结果，故需研究系统不同的单次仿真时间对此基带系统抗噪性能的影响。故设置噪声方差Var=0.01 W，改变不同的单次仿真时间t，执行一次系统仿真所得误码率Pe的结果如图8。

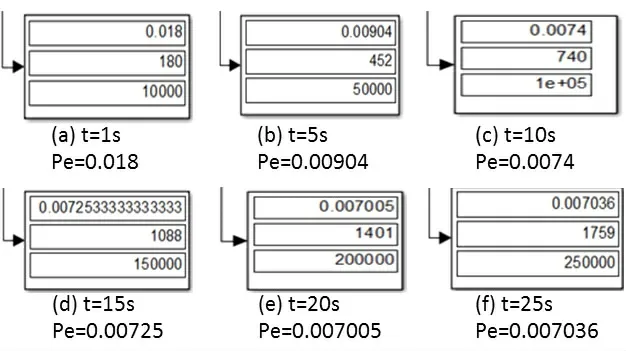
图8 单次仿真时间与基带系统误码率的关系

从图8可知，系统单次仿真时间需要设置大于10 s，误码率才能小于7e-3。另外，当单次仿真时间取15 s、20 s和25 s这三个值时，系统的误码率相当接近；并且当单次仿真时间设为25 s时的误码率反而比单次仿真时间为20 s的误码率更大了。考虑到系统仿真分析的效率，故选定此基带系统单次仿真时间为20 s，并在此基础上进一步研究此基带系统的误码率与噪声方差的关系。

在Matlab中可通过错误率统计模块（Error Rate Calculation）绘制此无ISI基带传输系统的误码率与噪声方差的关系曲线。为了获得此曲线图，需要编写一个M文件，通过运行此M文件多次调用系统仿真模型，从仿真结果中得到不同噪声方差值时的误码率，从而绘制出误码率曲线[6-7]。相应的M文件代码如下：

程序执行之前，需要将随机数发生器中噪声的方差Var设为变量sigma2。并将错误率统计模块输出的误码率值以变量Error形式传输到Matlab的工作空间。

M文件程序执行完毕，获得不同噪声方差值时的误码率曲线，相关曲线图如9。

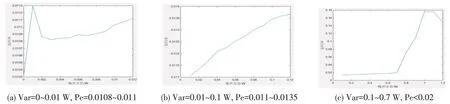
图9 不同噪声方差与误码率曲线（模型单次仿真时间t=20 s）

从噪声方差与误码率曲线来看，通过程序调用基带传输系统的Simulink模型进行仿真所得的误码率要比单次执行基带传输系统的Simulink模型进行仿真所得的误码率大，例如当噪声方差Var=0.01 W时，误码率曲线图中的误码率Pe≈0.011；而单次执行Simulink模型所得的误码率Pe=0.007005。对比分析原因有二：其一是程序调用方式得到的误码率是平均值，而单次执行Simulink模型所得的误码率是最后较稳定较精确的值。其二，通过程序调用基带传输系统的Simulink模型进行仿真所得的误码率要通过变量返回到Matlab工作空间，再调用画图语句画图所得，这过程也导致误码率增加。但是通过程序调用基带传输系统的Simulink模型进行仿真获得误码率方式具有明显的工程指导意义，从图9中的（a）和（b）来看，噪声方差Var<0.1 W时，误码率较小，且变化平缓。从（c）图中可知，噪声方差Var<0.7 W时，误码率Pe<0.02，而且变化也较平缓；当Var>0.7 W时，误码率Pe随噪声增大而明显地增大。

4 结论

首先阐述了数字基带传输系统的组成以及相关原理。其次利用Matlab/Simulink仿真平台，对无ISI基带传输系统进行系统建模、功能仿真和抗高斯噪声的性能分析。系统仿真步长为1e-4 s，信源传码率为1000 Baud。

仿真结果表明：在高斯噪声方差Var=0.01 W条件下，Matlab单次仿真的最佳时间为20 s，此时仿真数据点数充足，所得误码率Pe=0.007005。并且在Var=0.01 W条件下，接收信号的线迹清晰，眼图规整。从系统的噪声方差与误码率曲线来看，当Var<0.1 W时，误码率小，且变化平缓；当Var<0.7 W时，误码率Pe<0.02，而且变化也较平缓；当Var>0.7 W时，误码率Pe随噪声增大而明显地增大；此结果在工程领域的参数计算及性能优化方面极具指导价值。