基于自适应遗传算法的层合板铺层优化设计

杨洋，代文猛，年春波

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

复合材料主要由树脂基体和增强纤维组合而成，因其具有比强度高、比刚度高且具有良好的可设计性能等优点，纤维增强复合材料在工业领域得到越来越广泛的应用[1-3]。复合材料的可设计性能主要体现在充分利用复合材料铺层的各向异性特性和结构的压层特性上，在复合材料结构的设计过程中，通过调整复合材料各角度铺层的顺序和百分比可以得到满足设计要求的最优结构。然而铺层优化设计并不是简单的线性函数求解问题，而是离散的层叠顺序优化设计问题[4]，该类问题具有很大的解空间并且其解具有无序性和干扰性。传统思路是建立大量的铺层结构而后逐一验证，其成本较高、效率较低。

遗传算法是模仿自然界“优胜劣汰，适者生存”的生物进化机制，运用计算机技术发展起来的随机全局搜索和优化算法，既适合于线性问题又适合于非线性问题的求解，尤其适合于离散设计变量优化问题以及混合离散设计变量的复杂优化问题。目前遗传算法在复合材料结构的优化设计方面得到了越来越多的国内外研究人员的重视[5-9]。冯消冰等[10]针对铺层结构参数具有离散型的特点，采用整数编码策略并针对结构强度优化的目标构造适应度函数，应用遗传算法对大型风机复合材料叶片进行了铺层优化设计。设计的结果表明，在铺层的优化设计中应用遗传算法是可行和可信的。丁玲等[11]采用整数编码的遗传算法研究了无人机机翼复合材料蜂窝夹层结构蒙皮的铺层优化问题，并通过有限元分析和静力试验验证了优化结果的有效性。武佳男等[12]利用MATLAB编程联合ANSYS有限元分析对复合材料声呐导流罩铺层结构进行优化设计，结果表明优化设计后的声呐导流罩强度性能显著提高。史旭东等[13]通过MATLAB调用Patran进行建模分析，编写遗传算法程序对大展弦比机翼进行结构优化设计。然而上述遗传算法收敛效率低，可靠性差，故而本文基于改进自适应遗传算法对层合板铺层进行优化设计。

1 自适应遗传算法

针对遗传算法早熟、收敛慢、可靠性低的缺点，提出了一种新的概率调整算法：当某些个体的适应度Fi大于平均适应度Favg时，为了加快淘汰劣质基因和不良个体，需增大交叉概率Pc和变异概率Pm；当某些个体的适应度Fi小于或等于平均适应度Favg时，为了保留优良基因和优秀个体，需降低Pc和Pm，即：

(1)

(2)

式中：Pc0为基础交叉概率；Pm0为基础变异概率。

当Fi≤Favg时，(Fmax-Fi)/(Fmax-Favg)≥1，故需要设定Pm和Pc的上限。此处规定Pc≤1，Pm≤0.1。

2 层合板铺层优化算法设计与实现

基于自适应遗传算法的复合材料层合板铺层优化算法设计以经典层合板理论为基础，以遗传算法为核心，以MATLAB与ABAQUS联合使用为主要实现平台，主要实现过程包括编码、设定初始种群、给定约束条件、有限元分析、计算适应度、遗传操作、追踪遗传算法性能等7个方面。

a) 编码。由于复合材料层合板铺层优化的变量为离散变量，而遗传算法的整数编码策略在解决离散变量的寻优问题时具有独特的优势，因此本文采用整数编码方式对允许使用的[0°/45°/-45°/90°]铺层进行编码，即[0/1/2/3]分别代表角度为[0°/45°/-45°/90°]的铺层。

b) 初始化种群。设定初始种群数目、最大遗传代数、种群代沟、交叉概率、变异概率等遗传算法相关参数。

c) 约束条件。复合材料铺层结构的设计一般需要考虑以下两个原则：

1) 同一复合材料构件中应包含[0°/45°/-45°/90°]4种角度铺层，以应对复杂的受载情况。

2) 同一铺设角的单层连续铺放，其层数不得超过4层，以免引起树脂基体开裂以及层间应力增高。

d) 有限元分析。首先在MATLAB中依据种群中不同个体的编码基因状况修改有限元分析模型的INP文件，更新各角度铺层的分布情况，然后调用ABAQUS进行有限元分析，并输出分析结果。调用方式如下：

! abaqus job=Job-laminate

system(′abaqus cae noGUI=abaqus2.py′)

使用MATLAB读取层合板各节点处的应变值，并保存最大应变量作为该个体的目标值。

e) 计算适应度值。遗传算法通过对目标值分配适应度值确定相应个体被选中进行遗传操作的概率。文中利用ranking函数将个体适应度值进行排序返回。该函数能够按照个体的目标值由小到大的顺序进行排序，并返回包含个体适应度值的列向量。

FitnV=ranking(-ObjV)

f) 遗传操作。通过select函数依据个体适应度值选择个体组成子代种群SelCh，个体的适应度值越大，则被选中的几率越高。

SelCh=select(′sus′,Chrom,FitnV,GGAP)

通过recombin函数依据交叉概率RecOpt对子代种群染色体进行基因交叉重组操作并返回新的种群。

SelCh=recombin(′recdis′,SelCh,RecOpt)

通过mutbga函数依据变异概率MutOpt对子代种群染色体进行基因变异操作并返回新的种群。

SelCh=mutbga(SelCh,FieldDB,MutOpt)

因为代沟的选择作用使得子代种群规模小于原始种群，故需要对子代种群大小进行恢复。这里采用恢复函数reins进行恢复。

[Chrom,ObjV]=reins(Chrom,SelCh,1,1,ObjV,ObjVSel)

g) 追踪遗传算法性能，记录最优解。使用trace函数记录每一代种群的最大适应度值，并记录最优解，使用plot函数绘制出各代种群的最优解变化曲线。

具体流程如图1所示。

图1 流程图

3 算例及优化结果

为了验证该算法针对复合材料层合板铺层优化问题的有效性，选用100mm×100mm的单层厚度为0.25mm的16层层合板进行铺层优化设计。该层合板四边简支，上表面施加竖直向下的1MPa表面压强。初始种群数目为40，最大遗传代数为100，种群代沟为0.9，初始交叉概率为0.7，初始变异概率为0.05，材料选用AS4/9773复合材料，其材料参数如表1所示。分别使用经典遗传算法和经过改进过后的自适应遗传算法对该复合材料层合板进行优化设计。

表1 AS4/9773复合材料参数

单向载荷下的层合板铺层优化过程如图2所示。从图2中可以看出，随着遗传迭代次数的不断增加，目标函数值(即最大形变量)也在呈现阶梯式下降直至收敛于最小值。在11代以前，优化曲线一直在波动，说明遗传算法在最大限度地搜索全域铺层角度的排列组合。11代以后，优化曲线趋于平稳，说明在全部铺层方案中找到了相应的最优解。

从图2与图3自适应遗传算法与经典遗传算法的对比中可以看出，两者的优化结果相同，经典遗传算法需要迭代20多代左右才能收敛，而自适应遗传算法迭代运算至11代即收敛，展现了自适应遗传算法的快速收敛性。

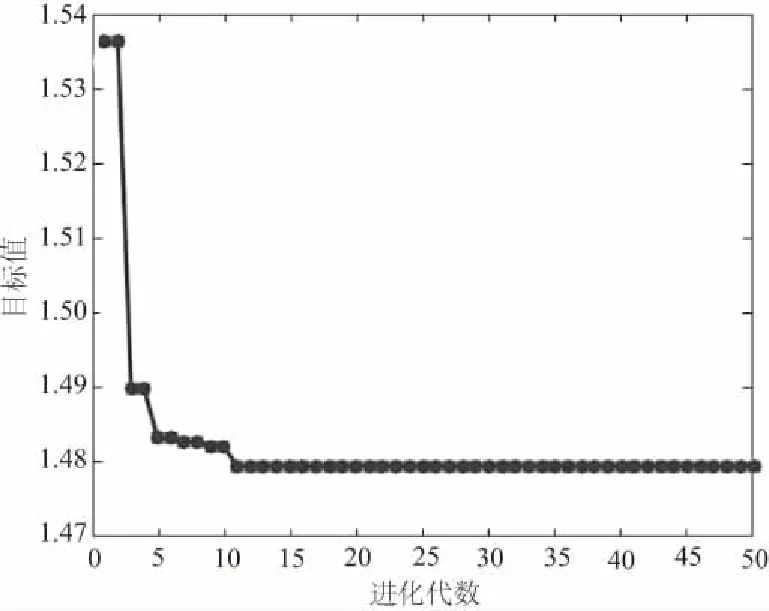
图2 自适应遗传算法

图3 经典遗传算法

表2所示的是铺层部分优化结果。在铺层优化的过程中，由于上表面施加的表面压强产生较大的剪切力，所以尽量保留了0°和90°的铺层，逐渐增加±45°铺层，用以抵抗横向载荷与纵向载荷。层合板的最大变形量从1.5361mm降低到了1.4796mm，可见层合板的强度有了显著的增强。

4 层合板铺层优化的有限元仿真验证

为了进一步验证优化设计的有效性，针对表2中所取得的优化铺层结果进行有限元仿真验证。将表2铺层部分优化结果中获得的铺层角度，利用ABAQUS软件进行有限元仿真以获得层合板最大形变量的变化趋势。

表2 铺层部分优化结果

图4为优化后层合板形变量云图。从4张对比图中可以看出层合板的最大形变量经过优化后在逐渐减少，说明层合板强度在不断提升。可以体现逐步达到优化目的。从自适应遗传理论中可以得出，经过不断优化，最大形变量最终值收敛于1.4796mm。最后一张云图显示形变量从外围向中部逐渐增大并在中心呈现最大值约是1.48mm，与算例中理论经过遗传迭代，最终趋于稳定值1.4796mm相一致，说明本文建立的优化平台可靠有效。

图4 优化后层合板形变量云图

5 结语

本文在复合材料力学经典层合板理论的基础上，借助ANSYS实现了复合材料的分析；以经典遗传算法为基础，提出了一种自适应遗传算法，通过MATLAB建立自适应遗传算法程序。两者相结合建立了复合材料铺层设计优化平台，并得到以下结论：

1) 以层合板最大形变量为优化目标，利用提出的自适应遗传算法，依据适应度值调整个体的交叉概率和变异概率，相比于经典遗传算法的优化方案提高了算法的收敛速度。

2) 以单向载荷下层合板铺层优化设计为例进行了验证，结果显示优化后的层合板最大形变量显著减小，并对优化结果进行有限元仿真，仿真结果表明，理论上优化后的最大形变量与实际层合板在该铺层角度下形变量相一致，验证了该优化平台的可靠性与有效性。