蒸发器除霜喷嘴的高压射流特性分析与结构优化
邢鹏成,丁武学,楼晓华,杨长春
(1. 南京理工大学 机械工程学院,江苏 南京 210094; 2. 四方科技集团股份有限公司,江苏 南通 226371)
0 引言
蒸发器广泛应用于制冷行业中,但在低温高湿环境下运行时,蒸发器壁面容易结霜。一方面霜层会增加蒸发器与空气的换热热阻,降低蒸发器换热效率,另一方面霜层会堵塞蒸发器的流通通道[1]。为了解决上述问题,需要定期对蒸发器进行除霜。蒸发器射流除霜过程通常包括2个阶段:第1阶段霜层加热,帮助融化;第2阶段喷嘴喷出高压气体通过射流击破冰霜。
在蒸发器除霜系统中,喷嘴起到能量转化的作用,即将压缩气体的压力能转化为射流动能,形成高压气射流对外做功。喷嘴作为能量转换部件,广泛应用于纺织、煤炭等多个领域中。陈巧兰等研究了不同孔径的喷气织机单圆孔辅助喷嘴的射流特性,优化了喷嘴结构参数,发现孔径最小的喷嘴能耗较低[2]。蔡毅等分析了直线型喷嘴和流线型喷嘴速度场和压力场的分布规律,发现流线型喷嘴的水射流出口速度大,动压大,破煤效率高[3]。胡俊等讨论了激光切割中喷嘴扩散段长度对流场参数的影响规律,发现扩散段存在一个最佳长度,压力能向动能转化效率最高[4]。目前,有关除霜喷嘴方面的研究较少。
为了提高喷嘴的除霜效率,本文设计了两种流道结构不同的喷嘴,采用理论计算和数值仿真两种方法获得了入口气压在0.3s内从0.6MPa快速降至0.1MPa时的喷嘴射流参数,并在此基础上,改进和优化喷嘴结构参数。
1 研究对象
除霜喷嘴由引流段l1、收缩段l2和扩散段l3组成。两种喷嘴结构参数如图1所示。1) 喷嘴收缩段为凹型圆弧收缩,引流段和扩散段呈圆柱状,计作喷嘴1;2) 喷嘴收缩段为直线收缩,引流段和扩散段呈圆锥状,计作喷嘴2。两种喷嘴长度为32mm,入口直径D为20mm,喷嘴1出口直径d为8mm,喷嘴2出口直径d为10mm。图中虚线区域为喷嘴收缩段与扩散段过渡区域。

图1 喷嘴结构参数
喷嘴入口连接储气罐,出口正对蒸发器结霜层,用0.2s喷射完储气罐中0.4m3的0.6MPa压缩空气,对蒸发器射流除霜。压强在0.2s后降至0.2MPa,在0.3s后降至0.1MPa。根据上述除霜方案,选取6组入口气压,分别为0.6MPa、0.5MPa、0.4MPa、0.3MPa、0.2MPa、0.1MPa,研究喷嘴入口气压在0.3s内从0.6MPa快速降至0.1MPa时的射流参数。
2 理论计算与数值仿真
2.1 理论计算
喷嘴入口和出口满足伯努利方程[5]:
(1)
式中:p1为喷嘴入口气压;p2为喷嘴出口气压;ρ为工作介质的密度;a为动能修正系数,本文喷嘴内流动为湍流,故取a1=a2=1;u1和u2分别为喷嘴的入口平均速度和出口平均速度;Δp为压力损失[6]。
根据文献[7]研究表明:压力损失以流道收缩处产生局部分离脱流为主,满足下式:
(2)
式中ξ为流阻系数。
根据文献[8]研究表明:ξ取值与喷嘴出入口面积之比有关。喷嘴1:A2/A1=0.14,取ξ=0.42;喷嘴2:A2/A1=0.25,取ξ=0.38。
喷嘴实际出口速度与理想出口速度满足[9]:
u3=μu2
(3)
(4)
式中:u3为喷嘴实际出口速度;μ为流速系数。
2.2 数值仿真
两种喷嘴的边界参数设置一致,出入口设置为压力边界条件,参考气压设置为0.1MPa,入口压力边界条件设置为喷嘴的入口气压,出口压力边界条件设置为大气压;固体壁面设置为无滑移边界条件,代入0.001mm的壁面效应;射流速度方向垂直于入口边界。两种喷嘴流场计算模型如图2所示。

图2 喷嘴流场计算模型
代入喷嘴入口边界条件分别为0.6MPa、0.5MPa、0.4MPa、0.3MPa、0.2MPa、和0.1MPa的理想气体,采用Simple算法、SSTk-ω模型、可压缩流,基于密度计算流体的平流和湍流特性。检查迭代收敛条件等各项参数和模型设置无误后开始求解,得到不同入口气压下喷嘴1和喷嘴2的流场计算结果。
3 射流特性分析
为研究两种喷嘴的射流特性,分别从湍动能、静压和出口速度3个方面分析喷嘴流场计算结果。
3.1 湍动能
图3为入口气压0.6MPa时,喷嘴1和喷嘴2的湍动能云图(单位:m2/s2)。可以看出:湍动能在引流段和收缩段趋于稳定,扩散段增幅上升,靠近出口位置处有最大值。喷嘴1的最大湍动能为2570m2/s2,喷嘴2的最大湍动能为5430m2/s2。
根据文献[10]研究表明:湍动能越大,湍流强度越高,能量损失越高。入口气压为0.6MPa时,喷嘴2的湍动能大于喷嘴1,能量损失高于喷嘴1。
不同入口气压下两种喷嘴的最大湍动能对比如表1所示。因其余入口气压下,湍动能分布规律相类似,故不再重复讨论。

图3 湍动能云图
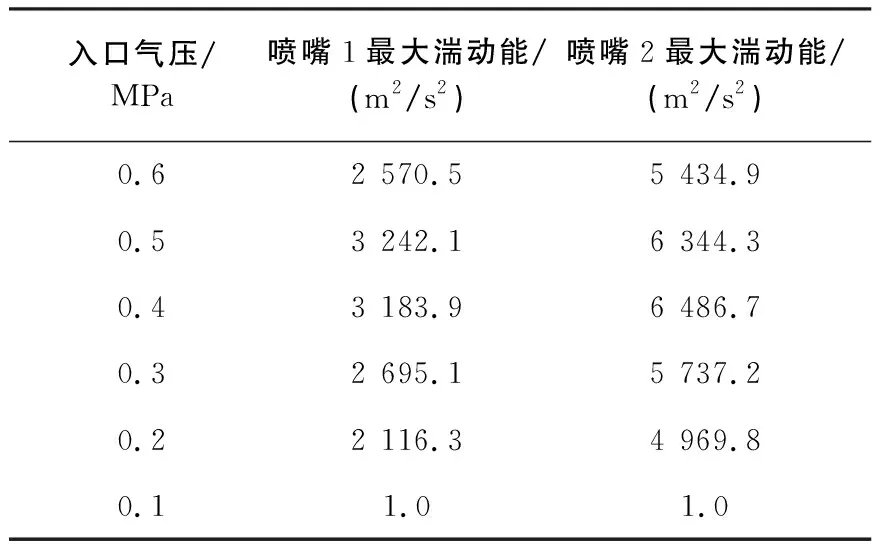
表1 最大湍动能结果对比
3.2 静压
图4所示为入口气压0.6MPa时,喷嘴1和喷嘴2的静压云图(单位:Pa)。可以看出:喷嘴1的静压沿轴向逐渐衰减;在过渡区域,喷嘴2的静压出现大幅度波动。
定义喷嘴气压波动幅度f,满足:
(5)
式中:ptmax为喷嘴过渡区域最高气压;ptmin为喷嘴过渡区域最低气压;pmax为喷嘴最高气压;pmin为喷嘴最低气压。
入口气压为0.6MPa时,喷嘴1的气压波动幅度f1=0.20,喷嘴2的气压波动幅度f2=0.75。喷嘴2的气压波动幅度较大,容易引起振动和噪声等问题。
不同入口气压下两种喷嘴的气压波动幅度对比如表2所示。因其余入口气压下,静压分布规律相类似,故不再重复讨论。

图4 静压云图
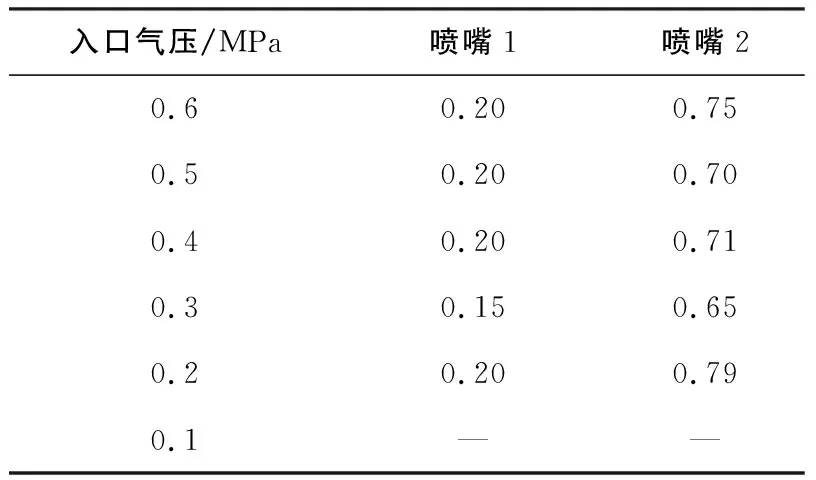
表2 气压波动幅度结果对比
3.3 速度
图5为入口气压0.6MPa时,喷嘴1和喷嘴2的速度云图(单位:m/s)。可以看出:喷嘴速度沿轴向逐渐增加,沿径向逐渐衰减,在出口处取最大值。通过数值仿真计算得到喷嘴1的出口质量平均速度为343.9m/s,喷嘴2的出口质量平均速度为477.1m/s。
入口气压为0.6MPa时,喷嘴2的出口质量平均速度优于喷嘴1。喷嘴2的流道结构较喷嘴1更能达到扩张提速的目的。
不同入口气压下喷嘴1、喷嘴2出口速度的理论计算和数值仿真结果对比如表3所示。可以看出:理论出口速度随p1的衰减逐渐降低。对于喷嘴1:当p1>0.3MPa时,出口质量平均速度将趋于固定值;而p1<0.3MPa时,出口质量平均速度随p1衰减而急剧降低。对于喷嘴2:当p1>0.5MPa时,出口质量平均速度趋于固定值;而p1<0.5MPa,出口质量平均速度随p1衰减而急剧降低。理论出口速度和出口质量平均速度数值接近。

图5 速度云图
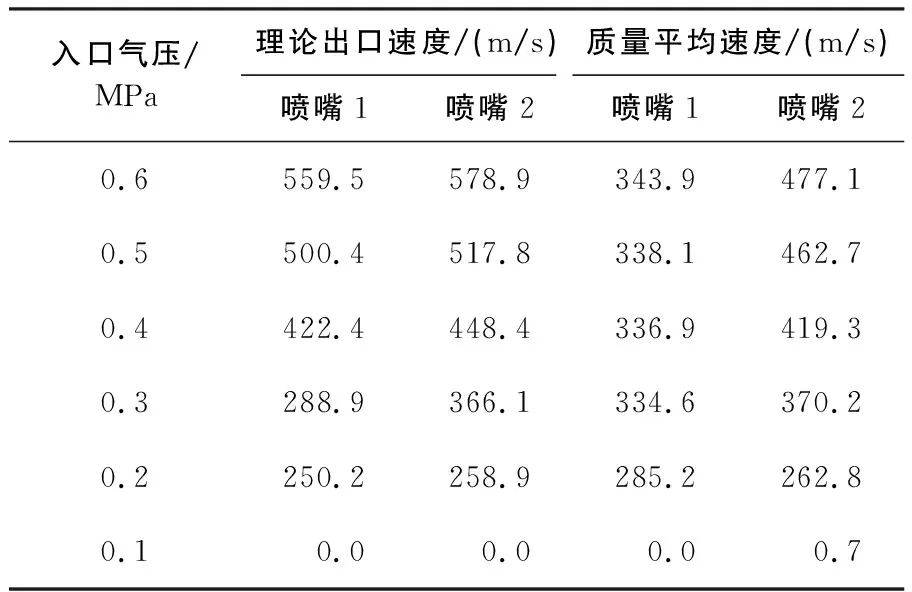
表3 两种喷嘴出口速度的理论计算和数值仿真结果对比
图6为喷嘴1和喷嘴2的出口质量平均速度随时间变化曲线。可以看出:
1) 0≤t<0.17s时,喷嘴2的出口速度优于喷嘴1;
2)t=0.17s时,两种喷嘴的出口速度相等;
3) 0.17s 图6 出口质量平均速度随时间变化曲线 综合喷嘴1和喷嘴2的结构特征和射流特性,改进喷嘴结构参数。喷嘴引流段通过样条曲线拟合而成,收缩段为凹型圆弧收缩,扩散段呈圆锥状,计作喷嘴3,其结构参数为:D=20mm,d=10mm,l1=2.81mm,l2=7.44mm,l3=21.75mm。 为了降低喷射过程中能量损失和气压波动幅度,同时保证出口质量平均速度不会受到影响,对喷嘴3的结构参数进行优化。 以喷嘴3为研究对象,r为设计变量,取5组数据r=8mm、r=9mm、r=10mm、r=11mm、r=12mm,湍动能、气压波动幅度和出口质量平均速度为优化目标设计优化方案。研究喷嘴3入口气压在0.3s内从0.6MPa快速降至0.1MPa时的射流参数。按照2.2节中流场计算方法计算流体的平流和湍流特性,得到不同入口气压下喷嘴3的流场计算结果。 表4和图7为入口气压0.6MPa时,喷嘴3的优化计算结果。从表4可以看出:当r=11mm时,喷嘴3的能量损失最低,气压波动幅度最小,出口质量平均速度较高。从图7可以看出:当r=11mm时,喷嘴3的能量损失低于喷嘴1和喷嘴2;气压波动幅小于喷嘴1和喷嘴2;出口质量平均速度优于喷嘴1和喷嘴2。其余入口气压下,喷嘴3的优化计算结果与此相类似,故不再重复讨论。 综上所述,当r=11mm时,喷嘴3的射流除霜能力优于喷嘴1和喷嘴2,除霜效率较高。 表4 喷嘴3的数值仿真结果 通过对蒸发器除霜喷嘴进行高压射流特性分析和结构优化,得到如下结论:1) 在0.3s的喷射过程中,喷嘴2的湍动能高于喷嘴1,能量损失较高;喷嘴2的气压波动幅度大于喷嘴1,易引起振动和噪声等问题;喷嘴2的出口质量速度优于喷嘴1。2)当r=11mm时,喷嘴3的射流除霜能力比喷嘴1和喷嘴2好,除霜效率较高。3) 本文关于除霜喷嘴的高压射流特性分析及结构参数优化可为除霜喷嘴的实际设计提供理论依据。 图7 r=11mm时喷嘴3流场计算结果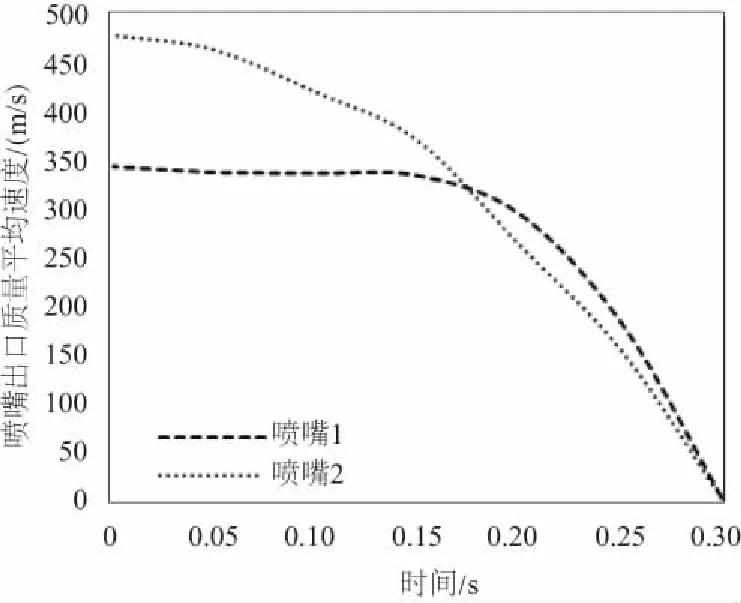
4 喷嘴结构参数优化
4.1 参数优化方案
4.2 优化结果与讨论

5 结语


