新型液压式动力反共振隔振器的试验研究
邓雨河,龙新华
(上海交通大学 机械与动力工程学院,上海 200240)
0 引言
随着隔振技术在工业领域的广泛应用,低频线谱隔振问题已成为日益突出的研究热点和难点[1]。传统被动隔振系统能够较好地隔离中、高频振动,但低频隔振能力较差[2]。为了扩大隔振范围,需要减小系统刚度来获得低频隔振能力,但往往存在着系统稳定性和隔振效果的权衡问题[3]。利用惯性耦合的动力反共振技术针对特定频率的激励产生的惯性力与弹簧作用力相位相反,从而实现线谱振动的隔离[4]。FLANNELLY W.G[5]提出了一种机械式动力反共振器(DAVI),解决了直升机主减系统隔振频率低和静位移不能太大的矛盾[6]。HALWES.D.R等人[7-8]提出了一种液弹式动力反共振隔振器(LIVI),利用惯性液体在流动过程中产生的动压力和弹性力相互抵消,从而实现隔振效果,其采用流体作为惯性质量,结构更加紧凑。为拓宽隔振器的反共振隔振频带,N. F. Du Plooy[9]提出刚度可调的带空气弹簧的液压隔振器。
本文基于动力反共振隔振原理设计制作了一种新型液压式动力反共振隔振器,进行了一系列试验研究,验证反共振隔振原理的正确性。基于试验结果对原有的反共振隔振模型进行修正,进一步验证了隔振模型的合理性。为了调节隔振器的反共振频率,进行了在不同惯性质量、初始静压下的试验测试,基于试验结果提出兼顾反共振频率可调性与隔振效果的方法。
1 试验装置
液压式动力反共振隔振器由内筒、外筒、波纹管、惯性质量等部件组成,结构示意图见图1。其内筒和外筒通过橡胶硫化成一体,橡胶提供隔振器刚度且作为隔振器的密封件,隔振器封闭腔室内充满水等低黏性液体。隔振器基座与振源(液压振动台)刚性连接,负载(被隔振对象)与隔振器上端盖刚性连接,振源激振力由基座传至负载。
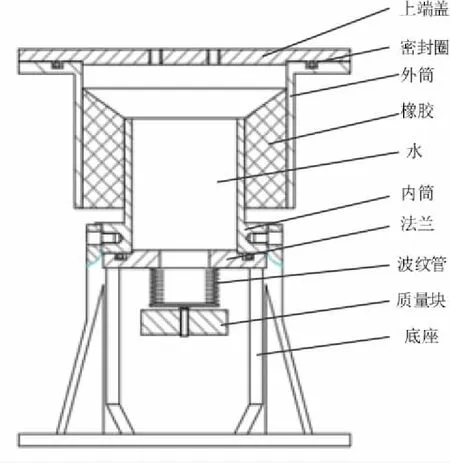
图1 液压隔振器结构
图2是隔振器试验装置,液压隔振器的试验特性与隔振器封闭腔室的液体初始静压有关[10],隔振器的进水泵口2与加压装置连接,通过调节加压装置进而改变初始静压。负载和惯性质量块仅在轴向上运动,两组传感器分别装在隔振器上端盖和内筒上。

1—上端盖1#传感器;2—进水泵口;3—液压传感器;4—上端盖2#传感器;5—内筒传感器。图2 液压隔振器试验装置
2 数学模型
液压隔振器包括固体、液体两种形式的材料,可以简化为机械DAVI隔振器力学模型。图3是液压隔振器的物理模型及其等效模型,其上液腔与波纹管通道面积之比等效于机械式DAVI隔振器中的杠杠比。隔振器外筒和被隔振对象连接,内筒和基础激励连接。被隔振对象质量为m1,内筒质量为m2,惯性质量块质量为m3,其位移分别为x1、x2、x3;外筒内直径、内筒外直径、波纹管直径分别为db、d0、da,其对应的截面积分别为Ab、A0、Aa;橡胶动刚度、波纹管刚度分别为k、k1,作用在内筒上的激励力为f。
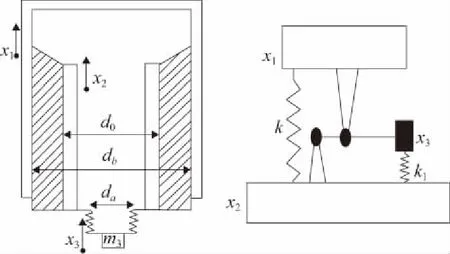
图3 液压隔振器物理模型及其等效模型
隔振器在受到外界激励时,隔振器的内筒、外筒、惯性质量块之间会产生相对运动,由流体连续性可知,运动前后上液腔减少的液体体积V1等于波纹管下液腔增加的液体体积V2,其中:
(1)
V2=Aa(x2-x3)
(2)
由V1=V2,得
x3=αx1+(1-α)x2
(3)
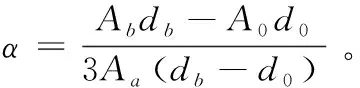
系统动能
(4)
系统势能
(5)
不考虑阻尼,由拉格朗日方程得到系统动力学方程有:
(6)
设外激励x2=X2ejωt,x2=X2ejωt,由上式可以得到隔振器的位移传递率
(7)
由式(7)可以得到
系统的共振频率
(8)
反共振频率
(9)
由式(9)可以看出,隔振器的反共振频率与隔振器橡胶动刚度、波纹管刚度、惯性质量及隔振器放大比有关,因此可以选择合适的隔振器参数,从而得到特定的反共振频率。
3 试验及理论对比分析
3.1 隔振器参数辨识
为了验证液压隔振器动力反共振理论,设计和加工了图1所示的液压隔振器,其具体尺寸为:da=25mm,db=136mm,d0=80mm,k1=20.59N/mm。通过隔振器无水情况下的振动试验可以拟合得到隔振器相关参数,图4是负载为13kg的频响曲线,表1是在不同负载质量下试验得到的隔振器固有频率。
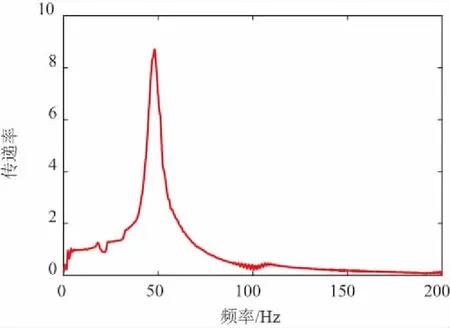
图4 无水情况下的振动传递实验曲线

表1 无水情况和不同负载下隔振器固有频率
得到以上隔振器参数后,进行隔振器有水情况下的振动测试,初步验证动力反共振理论。图5是在惯性质量为0.3kg、负载质量23kg下的振动测试试验结果,可以看出隔振器在42.2Hz的频率下具有较好的隔振效果。

图5 有水情况下的振动传递实验曲线
由式(8)和式(9)可以得到隔振器的理论共振频率38.2Hz和反共振频率43Hz,与图5中试验共振频率38.5Hz及反共振频率42.2Hz基本一致,但是试验结果中的二阶共振峰是式(7)中未出现的,为了对试验结果进行进一步理论分析,下面建立两自由度隔振系统对原隔振模型进行修正。
3.2 隔振器模型修正
参考文献[8]对液压式动力反共振隔振器建立的考虑隔振器体积刚度的机械式集中参数隔振器模型,在图3所示的机械杠杆式DAVI等效模型中考虑铰支点处的非完全刚性,对应铰支点处的位移为x4,其铰支点刚度对应液压隔振器中波纹管径向膨胀带来的隔振器体积刚度,其等效数学模型见图6。

图6 考虑隔振器体积刚度的等效数学模型
系统动能
(10)
系统势能
(11)
不考虑阻尼,由拉格朗日方程得到系统动力学方程式有:
(12)
设外激励x2=X2ejωt,x1=X1ejωt,由上式可以得到隔振器的位移传递率
(13)
进一步得到隔振器的反共振频率
(14)
令式(13)分母为0,可以得到隔振器的第一阶固有频率fp1和第二阶固有频率fp2。
由于隔振器的体积刚度ku未知,为了对以上隔振器动力学模型进行验证,采用参数识别法,将不同惯性质量m3下的反共振频率fz代入式(14)中,进而识别出未知参数即隔振器的体积刚度ku,进一步将参数代入共振频率fp1和fp2中,从而验证改进后的动力学模型的合理性。图7、图8是隔振器在惯性质量分别为0.3kg、0.6kg负载质量下的振动传递试验曲线。
由图7、图8可以看出0.3kg、0.6kg的惯性质量对应的反共振频率分别为42.1Hz、33.3Hz,将其代入式(14)中,可以拟合得到ku=123.39N/mm。进一步,可以求得fp1和fp2,其结果见表2、表3。

图7 0.3kg惯性质量不同负载的振动传递试验曲线
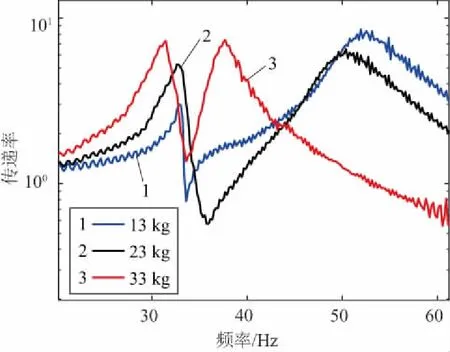
图8 0.6kg惯性质量不同负载的振动传递试验曲线

表2 0.3kg惯性质量不同负载下理论共振频率和反>共振频率与试验值对比
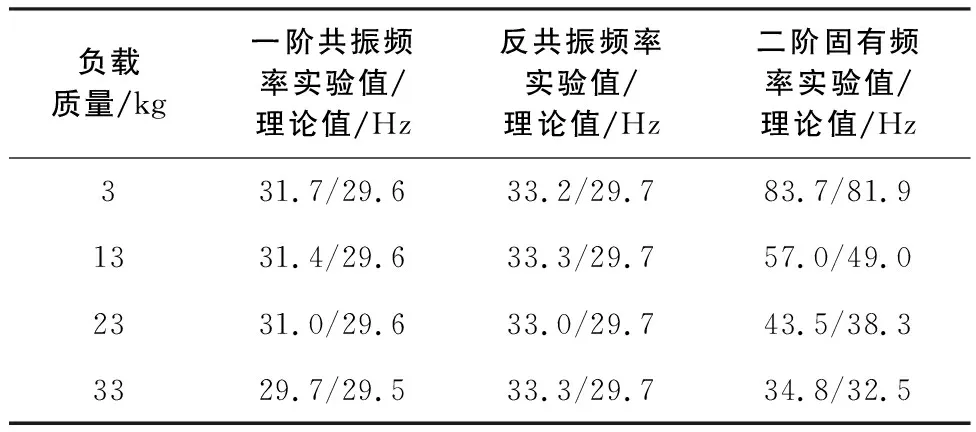
表3 0.6kg惯性质量不同负载下理论共振频率和反共振频率与试验值对比
由表2、表3可以看出,隔振器的共振频率及反共振频率理论值与试验结果基本一致,说明修正后的隔振器模型能够较好地预测试验结果。
3.3 初始静压影响性分析
文献[10]指出液压隔振器的隔振特性与液体初始静压有关,为了探究其关系,在不同液压下进行新型液压隔振器的振动传递试验:在惯性质量为0.9kg,在13kg、23kg、33kg不同质量的负载下,分别在隔振器初始液压为0.1MPa、0.2MPa、0.3MPa、0.4MPa的不同工况下进行振动传递试验,实验结果如图9-图11所示。

图9 负载13kg不同初始液压下的频响曲线

图10 负载23kg不同初始液压下的频响曲线

图11 负载33kg不同初始液压下的频响曲线
由以上试验结果可以看出,在惯性质量不变的情况下,增大隔振器液体的初始液压,隔振器的反共振频率点向右下侧移动,说明增大初始液压可以增大隔振器的反共振频率,并且可以进一步提高隔振效率。由修正后的液压隔振器模型可以知道,隔振器的共振频率和反共振频率与隔振器的体积刚度有关,隔振器的体积刚度会随着隔振器液体的初始静压增大而增大,从而影响隔振性能。
4 结语
本文设计制作了一种新型液压式动力反共振隔振器,进行了大量试验研究,并与理论分析进行比较,得到如下结论:
1) 考虑隔振器体积刚度的新型液压隔振器模型能够较好地预测隔振器试验结果,较单自由度集中参数模型能够更好地预测系统的二阶共振峰值。
2) 新型液压隔振器的反共振频率可通过调节惯性质量的大小来实现,隔振系统的两阶共振峰值都会随着负载的增大而减小,但对反共振频率没有影响。
3) 隔振器的初始液压影响着隔振效果,合理增加初始液压能够提高隔振效率。

