Spatial Fractal Properties of Loess Plateau in the Northern Shaanxi Province of China Kamila J
-, , , ,
(1.School of Geography,Nanjing Normal University,Nanjing 210023,China) (2.School of Geosciences,University of Energy and Natural Resources,Sunyani 214,Ghana) (3.Earth Observation Research and Innovation Centre(EORIC),University of Energy and Natural Resources,Sunyani 214,Ghana) (4.Key Laboratory of Virtual Geographic Environment of Ministry of Education,Nanjing Normal University,Nanjing 210023,China) (5.Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application,Nanjing 210023,China)
Abstract:The Loess Plateau of the Northern Shaanxi Province of China is an important area of research for geomorphological studies. Several studies have been conducted in the past in this particular subject of geomorphology. However,spatial variability of fractal dimension(FD)vis-à-vis its relationship with landform characteristics have been limited. Thus,the paper assessed the application of fractal methodology to investigate the fractal properties the terrain and stream networks. The results show that Grid Size(GS)for the FD estimation affects the distribution of the values obtained. It was recommended that for the Loess Plateau understudy,a GS of 32 was realistic and mimics well with the landform classification types provided by other studies. The GS of 16 and 64 underestimates and overestimates the FD respectively. The FD values for the stream networks indicate that Strahler Numbers(SN)and FD are related. For instance,the higher SN,the higher FD. However,a more in-depth analysis of the SN and FD needs to be conducted in future studies. The findings from this study could provide a baseline support for future research on geomorphology in the Loess Plateau and support for other regions interested in similar work.
Key words:digital elevation model,grid size,fractal dimension,Strahler number,landform types
CLCnumber:P208Documentcode:AArticleID:1001-4616(2020)02-0056-07
陕北黄土高原地貌空间分形特征
卡米拉1,2,3,汤国安1,4,杨 昕1,5,那嘉明4,5,熊礼阳1,5
(1.南京师范大学地理科学学院,江苏 南京 210023) (2.能源与自然资源大学地球科学学院,加纳 苏尼亚尼 214) (3.能源与自然资源大学地球观测研究和创新中心,加纳 苏尼亚尼 214) (4.南京师范大学虚拟地理环境教育部重点实验室,江苏 南京 210023) (5.江苏省地理信息资源开发与利用协同创新中心,江苏 南京 210023)
[摘要]陕北黄土高原因其地貌类型既丰富又典型,是地貌研究的重要区域,已有不少关于本地区的地貌研究成果. 然而对分维值的空间分异及其与地貌特征之间的关系的认识还十分有限. 因此,本文评估了用分形方法探索地形和河网的分维特征的应用适宜性. 结果显示,计算分维值的窗口大小影响结果的空间分布特性. 当格网大小为32时是最适合黄土高原地区的分维值估算,其结果与其他研究展示的地貌分类一致. 网格大小分别为16和64时,会产生高估或低估分维值的结果. 对河网的分形研究表明,分维值与Strahler级数相关,河网级数越多,分维值越大. 河网结构的分形特征还有待进一步研究. 本文研究成果可为地貌特征和其他地区的分形研究提供参考.
[关键词]数字高程模型,格网大小,分维数,Strahler 级数,地貌类型
Receiveddata:2019-03-29.
Foundationitem:Support by the National Natural Science Foundation of China(41930102,41771415),the Priority Academic Program Development of Jiangsu Higher Education Institutions(164320H116).
Correspondingauthor:Yang Xin,PhD,Professor,majored in digital terrain analysis. E-mail:xxinyang@njnu.edu.cn
doi:10.3969/j.issn.1001-4616.2020.02.010
Digital Terrain Models(DTMs)provide an easy simple data structure that allows for easy and effective extraction of terrain derivatives and hence has led to the wide acceptability and use of DTMs for geomorphological studies,hydrology and soil science[1]. Geomorphological features include points,lines and polygons such as peaks,ridges,saddles and gullies on the land surface that help to classify landform types. Such features control the spatial geomorphology of a particular place in question. Several Chinese scholars have proposed the extracting of geomorphological points from DTMs,typically from Digital Elevation Models. Typical examples include extraction of saddles based on runoff concentration simulations or extreme elevation points along water-shed boundaries[2]. Watershed hydrology is one of the key components of geomorphometry. For instance,surface geomorphometry affects the water flow regime,flow generation and the routing in the watershed hydrology. Differences in terrain,also affect the spatial dynamics of the hydrological characteristics. DEMs have been used for hydrological modelling and prove to be an important entry point for geomorphometry studies[1,3].
One of the emerging techniques,has been the application of fractals to improve understanding of hydrological regimes and geomorphological feature complexity. The word fractal invented by Mandelbrot was to bring together under one umbrella of objects that have certain structural features in common,regardless of their appearance in geography,astronomy,fluid dynamics,probability theory and pure mathematics[4]. This fractal phenomena has received several attention in the field of mathematics,biology and geomorphology[5-12]. It has evolved to become new for traditional applied mathematics and a revolution in topological space theory research,which is applicable for simulating and characterizing landscapes precisely by using mathematical formulae[13].
The integrated and cumulative influence of various geological processes result in the formation of topographic features[14]. The spatial entities are the result of different features such as in shape,size,and relief. Fractal properties of geomorphic features have been investigated by several authors such as slopes[15],coral reefs[16]and river networks[17]. In landscape research,fractal measurements provide information about the space-filling properties of a mosaic of patches at all scales. The fractal dimension,FD,provides a characteristic variable to indicate the variation that is useful in terms of the processes influenced by development. In order to estimate the fractal dimension of any linear phenomenon,variety of methods exist. These include box counting,triangular prism areas,projective covering method and fractal Brownian model[18-21].
In this paper,we assessed spatial fractal properties of stream networks in the Loess Plateau in the Northern Shaanxi Province. Terrain complexities in general are shaped by various riverine processes on the landscape indicating their degree of importance of rivers and streams. The degree of complexity of the fractal properties of the stream networks would inform about unit of complexity of such a geomorphic feature. Therefore,the research findings would bring to fore,deeper understanding of differential changes in geomorphological features. This could also be used in conjunction with traditional methods for improved interpretation and understanding of landform complexity.
1 Materials and Methods
1.1 Study area and dataset
The Northern Shaanxi region is dominated by continental monsoon climate but with some regional disparities. The average annual precipitation is 570 mm. This falls within the period of July-October. The climate is characterised by warm,windy spring when the temperatures rise steadily. The average annual temperature is 13.8 ℃. The main rainfall occurs in the periods in July-September. The study area is located between 107°28′E-111°15′E and 35°20′N-39°34′N showing the middle belt of the Loess Plateau(See Fig.1). The Advanced Spaceborne Thermal Emission and Reflection Radiometer(ASTER)Digital Elevation Model(hereby referred to as GDEM2)was obtained from the Earth Explorer[22].
1.2 Box counting method(BCM)
The BCM is mostly used to determine the fractal dimension. It has been widely used to determine area of irregular cartographic features. It is sometimes called the grid or reticular cell counting method[19]. The box counting approach has been applied to many several studies about streams,coastlines and linear features[21]. The general mathematical form of the box counting method is:
N(r)=Cr-D,
(1)
whereDis the fractal dimension,N(r)is the number of boxes that cover the linear object measured,ris the side length of the square box andCis the constant. The log-log form of this equation is:
log[N(r)]=-Dlog(r)+log(C).
(2)
To obtain the truthful value ofD,one needs to count theN(r)for different side lengths ofr,then obtain theDfrom the data pairsN(r)andrusing least square regressions. This method works best for self-similar linear objects. The primary data form used with this method,is grid-based DEM.
Some challenges have been identified with the standard application of the method as it depends on significant computation power. To overcome the large computation problems associated with this method,an automated Matlab function was developed to allow for the automatic unsupervised box counting[5].
1.3 Selection of grid size and stream networks
The ASTER DEM was used to delineate watersheds of approximate equal areas of 10 km2. This was to ensure easy comparison for the terrain complexity of the watersheds. About 124 sub-watersheds were created for the study area. Out of this number,a selection of 12 representative sub-watersheds’ stream networks were selected. Each of the stream network was denoted per the location presented in Fig.1 as SNet(1). This implies SNet(1)denotes a stream network within location(1)of the sub-watershed under discussion.
The fractal dimension estimation is scale dependent and this is particular true for different grid sizes. Some researchers have mentioned the importance of this scale effect on the fractal dimension estimation[13,23-25]. Therefore,in this paper,three Grid Sizes(GS)were considered—16,32 and 64. The comparison of the effect of the GS on the FD estimates also provided some understanding to deciding the appropriate scale adequate for the purpose of this study.
2 Results and Discussions
2.1 FD in the Northern Shaanxi with varied grid size
Fig.2 shows the fractal dimension for Grid Size(GS)of 16,32 and 64. The GS=16 shows an FD behaviour of minimum of 2.00 and a maximum of 2.53 with a mean value of 2.09. The spatial distribution of the frequency shows two distinct peaks divided between 2.00-2.11(21.7%)and 2.11-2.53(78.3%). In contrasts to the GS=32,where the minimum FD is 2.03,maximum value of 2.51 with a mean of 2.12. The FD for GS=32 shows three zones as 2.03-2.13(14.8%),2.13-2.28(20%)and 2.28-2.51(65.2%). The GS=64 shows more contrast compared to the GS=32. Its minimum FD is 2.07,maximum of 2.56 with a mean of 2.16. The histogram distribution shows principally two zones of 2.07-2.37(33.6%)and 2.37-2.56(66.4%). The standard deviation(SD)for the GS of 16,32 and 64 respectively are 0.13,0.17 and 0.20.
Twelve locations as indicated in Fig.1 were selected as a means to validate and compare other findings in this research and also with other studies. The notation SNet(x)has been used to denote each of the locations. This implies that location(1)becomes SNet(1). Thus,the values of the FD at each of these locations were extracted for validation and comparison with other studies.
For instance,for SNet(7),the FD shows 2.21(16),2.17(32)and 2.29(64). This shows a comparative increase of FD as the GS increases. This location is the core area of the Loess Mountains with a relative erosion in the range of 500-10 000 t/m2per year[26]. Therefore,the GS=64 appears to estimate much higher FD compared to the rest. Of course,this GS aggregates more terrain surfaces within a window for analysis and hence indicates the reason for its estimation of high values.
Another example is SNet(8)characterised by erosion amounts of 20 000-25 000 t/m2per year. The spatial FD shows 2.2,2.33 and 2.34 respectively for GS(16,32 and 64). Again,it is clear that the grid 64 has slightly higher values compared to the 16 and 32.
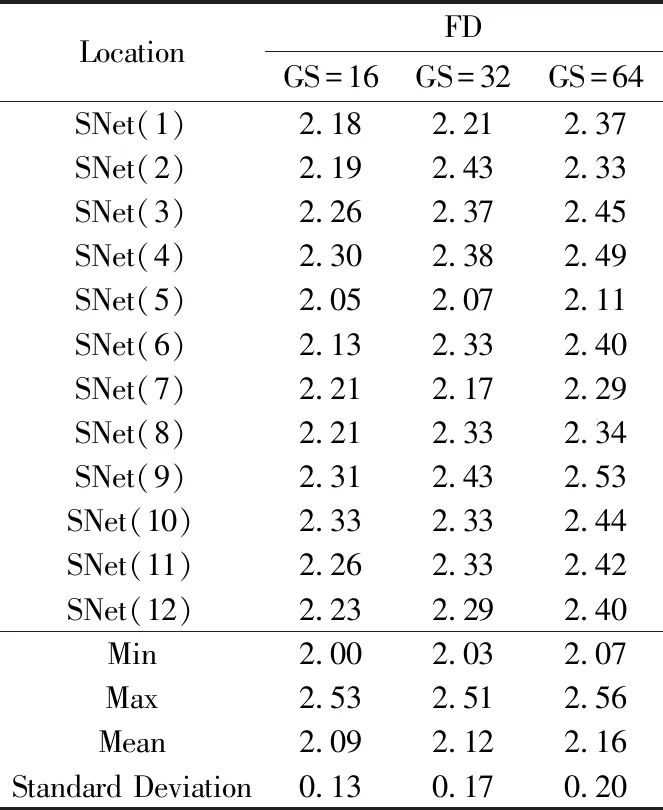
Table 1 Comparison of FD for GS of 16,32 and 64 grids at 12 locations
The SNet(1-6,9-12)shows similar trend across as shown in Table 1. It implies that the FD for 16,32 and 64 varies incrementally across the GS used for the estimation of the FD. A closer look at the 32 grid reveals that this GS provides a much better representation in terms of space and distribution across the various landforms,mapping out the hilly-mountainous areas and the desert areas more closely. The expectation is that,hilly and mountainous regions should have much higher FD compared to desert regions. The GS=16 and GS=64 do not reflect this case. In this case,the SD of 0.17 may appear acceptable for the FD estimation. Though GS=16 gives a lesser SD variation within the datasets,the variation of 0.17 seems much close to reality as to the representation of the FD.
The overall findings show that FD values are site specific and has a strong relationship with the grid size used. Therefore,it is important that for every specific landform,to select the best grid size that suit the landform type. The GS of 32 was found to provide reasonable estimates and hence was recommended for use in this study area.
2.2 Spatial pattern of FD in the Northern Shaanxi
The Northern Shaanxi is characterised by various changing landforms spread across the study sub-areas. These include-loess tableland ridge,loess tableland,rocky hill ridge,loess middle-low Mountain,loess hill-ridge,loess low-hill,loess incision gorge-hill and desert-loess transitional area. Nine classes were divided into three for easy explanation of the findings-Southern Belt(SB),Middle Belt(MB)and Northern Belt(NB)(Fig.3). The SB comprises primarily of loess tableland-ridge and loess tableland. The MB comprises of loess ridge,loess hill-ridge and loess-low Mountain while the NB comprises of the loess hill ridge,desert loess transitional area and loess incision gorge-hill. The spatial pattern of the FD was categorised into three continuous intervals[2.00-2.19],[2.20-2.34]and[2.35-2.51]. The NB is characterised by fractal values mostly shared evenly between[2.00-2.19]and[2.20-2.34]with few pockets of parcels between[2.35-2.51]. This corresponds to the landform characteristics of hills and desert loess forms. The MB is characterised by mostly fractal values of[2.34-2.51]representing the complexity of the various mountainous landforms in this region. The SB is a complex mix of various forms sparsely distributed between the[2.00-2.19],[2.20-2.34]and[2.35-2.51]. The spatial correlation between the FD and elevation characteristics was found to be(R2=67%),indicating that,FD is able to characterise the terrain complexities.
2.3 Fractal dimension of stream networks
Fig.4 and Table 2 show the variation of the various river networks for the selected 12 sites in the Northern Shaanxi Province of China. In the case of SNet(7)the watershed area is 1 070 km2with a Strahler Number(SN)of 4. The FD shows a fractal value of 1.30 within a possible dendritic river network. The dendritic nature indicates the complexity in the watershed and a sign of possible intense erosion potential. Case of SNet(8),a smaller watershed area of 401 km2,it shows a simple structure with a SN of 2 and a low FD of 1.15. In comparison to SNet(8),SNet(7)has a larger watershed area with larger complexity and thus,a higher FD.
In the case of SNet(9),the catchment has an area of 1 220 km2with SN of 3 with a FD of 1.26. The FD is smaller compared to SNet(7)with SN of 4. The possible reason for this higher FD of SNet(7)compared to SNet(9),could be the result of the fact that,higher SN implies more complexity. Therefore,the higher the SN,the higher the FD. Case SNet(10)is similar to SN compared to SNet(7). However,SNet(10)has a smaller catchment area of 419 km2almost half of SNet(7)and shows a parallel river network. This gives a FD of SNet(10)as 1.23.
Case SNet(11)has a FD of 1.23 and SN of 3 and a catchment area of 604 km2. This FD behaviour is similar to SNet(1). There is a slight variation in the catchment area. SNet(2)shows a slightly higher FD of 1.24 as a result of the slightly larger catchment area of 739.6 km2. SNet(3)has a catchment area of 436.7 km2and an FD of 1.19 and SN of 3 but a simple structure. This simplicity of structure is related to the small FD obtained. Cases SNet(3,4,5 and 6)all have the same SN of 3 and catchment areas of 436.7 km2,942.5 km2,629.8 km2and 507.7 km2respectively. SNet(3)has a smaller area and hence has a smaller FD of 1.19. All other have similar FD of 1.25-1.26.
The higher the strahler numbers,the higher the fractal dimension values obtained. This implies,some relationship between the SN and FD values. A more detailed study of the relationship between the SN and FD could be investigated in future studies. Other studies such as Khanbabaei et al. attempted to study the relationship between the FD and some geomorphological and found that,the river branching could be investigated,as a way to further establish the direct link between them[27]. Rivers characteristic patterns in terms of the level of branching(dendritic,trellis,parallel)do have an influence on the FD values obtained. Thought,there was not in-depth studies on the river network patterns and their influence on the FD,it can be shown that,the denser the river pattern,the higher the FD obtained. The FD is also related to the catchment area. Larger catchment areas tend to have higher FD values. Earlier studies from Rosso et al. have confirmed the relationship between the length and area;and hence the derivation of FD functions were implemented[28].

Table 2 FD and stream network characteristics
3 Conclusion
Several studies have been conducted in the Northern Shaanxi Province of China in respect of geomorphological studies. However,the application of modern techniques such as fractal geometry to provide additional insights to landform complexity and dynamics has been limited. Thus,this paper assessed the spatial variability of terrain and stream networks using estimation of fractal dimension. The comparison of the fractals from the terrain and stream networks are further compared and interpreted. The findings show that the FD for the terrain are site specific and has a strong relationship with the GS used. Therefore,for every terrain,it was imperative to investigate and select the best GS to suit the particular landform type. The spatial distribution of FD for the study was developed and showed close proximity with the various landform types identified in previous studies. This explained that FD can play a key role in the classification and further deeper interpretation of the landform in terms of its proneness to anthropogenic and other natural transformations such as erosion processes. Another finding was that,the degree of the Strahler Numbers corresponded with the fractal dimension values. This was comparable to other studies that say river branching provide useful information for its complexity. The authors anticipate that the findings from this work would be useful for supporting other studies interested in understanding the anthropogenic nature of the Loess Plateau in the Northern Shaanxi Province of China.

