求解Klein-Gordon方程的新型快速紧致时间积分方法
黄建国,吴 渤
(上海交通大学数学科学学院,上海 200240)
Klein-Gordon方程是一类典型的非线性波动方程,在理论和应用物理的许多领域,如非线性光学、固体物理和量子场论[1-2]中有广泛应用. 本文考虑如下Klein-Gordon方程:
(1)
式中,Ω⊂R2是有界矩形区域,D>0是扩散系数,g是非线性函数,f是外源函数.
近年来已有学者对Klein-Gordon方程发展了各种数值方法. 例如差分法[3-4],边界元法[5],微分求积法[6]等. 然而这些现有的数值方法要么精度有限,要么计算复杂度大,因此很有必要发展求解该问题的高效计算方法. 最近,作者在文献[7]中借鉴积分因子方法[8-13]的思想提出了一种快速紧致时间积分法(FCTI)用于数值求解任意阶发展方程. 该方法在空间方向使用紧致差分格式离散,然后在时间方向上基于快速离散正弦变换和常数变易公式获得任意阶发展方程的显式表达式,再利用Lagrange插值近似非线性源项,导出了一类高效求解方法. 本文将使用前文方法数值求解Klein-Gordon 方程(1),但用Hermite 插值代之于 Lagrange 插值来处理非线性源项,从而得到更为高效的数值求解方法. 此时,仅需利用前两个时间步的计算结果,就可获得空间和时间方向均为四阶精度的高效算法. 数值实验验证了所提算法的高效性.
1 空间离散:紧致差分格式
设Ω={xb (xi,yj)=(xb+ihx,yb+jhy),0≤i≤Nx,0≤j≤Ny. 给定正整数p,记 并定义如下两个算子: 使用四阶紧致差分格式进行空间离散[14-15]: 式中,i=1,2,…,Nx-1,j=1,2,…,Ny-1,从而得到方程(1)的如下空间半离散化格式: (2) 式中, 经直接计算可知,在方程(2)中出现的相关矩阵存在以下谱分解: 又记H=(hi,j)(Nx-1)×(Ny-1), (3) 则注意到hi,j<0,从而易知 定义g(t)=(gij(t))(Nx-1)×(Ny-1),g′(t)=(g′ij(t))(Nx-1)×(Ny-1). 设V(t)=U′(t). 则使用文献[7]中相同办法,利用常数变易公式可知问题(3)之解可显式表示为 (4) 给定正整数Nt,设 Δt=T/Nt. 对时间区间[0,T]做均匀剖分:tm=mΔt,m=0,1,…,Nt. 由(4)可得如下时间递进计算格式: 式中, 当r=0,1,2,3 时,记 式中, 定义 式中, 在此基础上,就可以得到求解(1)的Hermite型快速紧致时间积分方法如下: 式中, 设N=max(Nx,Ny),基于FFT算法实现以上数值解法,易知在每一时间步总的计算复杂度是O(N2log(N)). 在本节中,通过数值算例讨论快速紧致时间积分Hermite格式的收敛性和效率. 在方程(1)中,选取g(u)=u-u3以及适当的函数使得精确解为 u(t,x,y)=cos(x)cos(y)sin(t). 取空间区域为Ω=(-1,2π-1)2,求解时间为T=1. 此时相应的边界条件是非齐次的. 在表1中列出了U和V在不同时空剖分网格下的L2和L∞误差、收敛率和CPU时间. 从中可以看出该方法在空间和时间方向上都达到了四阶收敛率. 就CPU时间而言,从表中可以发现,由于使用了FFT算法,即使在空间网格非常细的情况下,CPU时间也非常小. 表1 在最终时刻T=1的误差、收敛率以及CPU时间Table 1 Numerical errors,convergence rates and the CPU times at T=1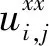

2 时间离散:时间积分和非线性源项离散
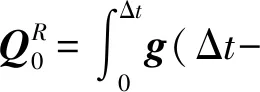

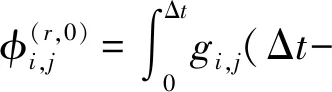
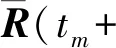

3 数值实验


