高中数学教学中数学抽象的表现与教学实践

王银娣

[摘  要] 在核心素养培育的背景之下，既然要培养学生的关键能力，那对数学抽象的理解就要再深入一步. 对数学抽象过程至少有三点深度理解：首先，数学抽象是学生对生活情境或原有数学知识的不同深度的思维加工;其次，数学抽象是用数学方法进行表征，用数学语言进行描述的过程;再次，数学抽象在知识与技能的体现、思维与表达的水准及交流与反思的表现上存在不同. 借助于数学抽象培养学生的抽象思维能力，利用抽象思维能力完成数学抽象，就是一个相互促进、相得益彰的过程.

[关键词] 高中数学;数学抽象;表现;教学

数学抽象是数学学科核心素养六个要素中的第一要素，也是一线教师研究数学学科核心素养的第一抓手，很多情况下对数学抽象的理解，就是将形象的生活事物转换成抽象的数学研究对象的过程，当转换后的数学研究对象能够纯粹地用“数”与“形”去进行描述时，那数学抽象的过程就认为是成功的. 从一般意义的角度来看，这样的理解没有问题，也是绝大多数高中数学课堂上数学抽象教学的常态. 但是笔者认为，在核心素养培育的背景之下，既然要培养学生的关键能力，那对数学抽象的理解就要再深入一步. 作为一线教师一般都知道，数学抽象是高阶思维加工的产物，而数学抽象的结果总有一定的表现形式，对其表现形式进行深度研究，可以让数学教学更好地通往核心素养的彼岸.

高中数学教学中数学抽象表现及理解

其实从学生学习结果的角度来看，学生的数学学习对象很多都是数学抽象的产物，因此数学抽象的主要表现为：获得数学概念和规则;提出数学命题与模型;形成数学方法与思想;认识数学结构与体系. 从这个角度来理解数学抽象，可以发现数学抽象的理解其实可以更加精细化，而以这些结果反推数学抽象的过程，结合《普通高中数学课程标准》中对数学抽象的水平划分与素养体现的界定，那对数学抽象过程至少有这样几点理解.

首先，数学抽象是学生对生活情境或原有数学知识的不同深度的思维加工，最终表现为数学抽象的水平不同. 高中数学知识体系当中，有些概念或规律直接来源于生活，而另有一些概念或者规律则来自学生已经掌握的相关概念，然后基于一定的逻辑关系进行的演绎，不同的知识对应的思维加工深度是不一样的，因此学生最终表现出来的数学抽象水平是不同的.

其次，数学抽象是学生对生活情境进行思维加工之后，再用数学方法进行表征，用数学语言进行描述的过程，思维水平的不同对应着不同的抽象结果. 数学抽象与数学表达不完全相同，数学表达是用数学语言描述数学抽象结果的，其强调的是数学语言的准确选择与运用;相应的数学抽象则是侧重于思维过程.

再次，数学抽象存在于数学概念的建立、数学规律的探究以及数学问题的解决过程中，學生在知识与技能的体现、思维与表达的水准及交流与反思的表现上存在不同.

例如，函数的单调性与最大（小）值教学中，数学抽象的起点往往是学生熟悉的函数，如一次函数或者二次函数;数学抽象的重点则是“函数单调性”概念的得出. 起点是学生比较熟悉的情境（对应着《课标》中数学抽象水平划分的“水平I”），得到的是“函数单调性”——包括概念、定义，以及相应的定义域的某个区间，尤其是单调增或单调减的逻辑关系等. 学生所理解的是数学抽象的结果，学生所记忆的则是数学语言表述的形式.

基于数学抽象表现实施高中数学教学

既然数学抽象的表现是不一样的，那在实际教学中就要根据数学抽象的不同表现，设计相应的教学过程. 在这个过程当中，数学抽象能力的培养又是关键. 数学抽象能力其实是一种通俗的说法，由于数学抽象与概括往往是结合在一起的，因此数学抽象概括能力由抽象和概括两部分组成，其是一种数学思维能力，是人脑和数学思维对象、空间形式、数量关系等相互作用并按一般思维规律认识数学内容的内在理性活动的能力，是高层次的数学思维能力. 下面来看一个例子. 在理解“增函数”和“减函数”概念的时候，应当重点设计两个方面：一是单调函数的文字表述;二是单调函数的图像表述. 文字表述主要是定义，虽然教学内容是增、减两种函数，但实际上引导学生理解和记忆的时候，只需要侧重于其中的一个（通常是增函数），而减函数的表述与图像，则可以让学生自己去推导、理解、记忆，这样可以减轻记忆负担，增强理解效果.

在设计增函数文字表述与图像表述的时候，考虑到学生的思维过程，具体设计应当是这样的：

首先，在分析一次函数和二次函数的基础上，帮学生回忆已经形成的关于单调增与单调减的初步认识（类似于默会知识）.

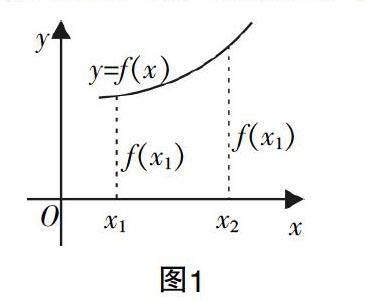
其次，对生成的经验进一步抽象，以形成精确的数学理解. 这里要强调定义域、区间、两个自变量x1和x2，以及对应的函数f（x1）和f（x2），当然也包括“如果x1>x2，那么f（x1）>f（x2）”的逻辑关系. 紧紧抓住这些要素而忽略其他，就完成了数学抽象的关键环节.

再次，将增函数的文字表述及理解，与相应的图像结合起来. 这是学生理解单调函数的时候容易忽视的一个环节，虽然大多数学生能够基于图像的形状判断出增减性，但是很少有学生将定义与图像结合起来. 这个环节非常重要，在教学中让学生在图（如图1）上将上述关键点标出，这样的一一对应，可以让学生对增函数的理解更加深刻与清晰.

从思维能力的角度理解数学抽象教学

从数学抽象表现的角度来看，文字与图像分属两种不同的表现方式，而从数学抽象的水平划分与素养体现来看，学生在上述数学抽象的过程中，实际上文字和图像是交替进行的：给出一次函数和二次函数的图像，让学生判断变化趋势，这是图像加工;从高中函数定义的角度理解函数的变化，这是文字加工;理解单调函数的定义，这是文字加工;将单调函数的定义与图像结合起来，又是图像加工. 如此交替进行，数学抽象就进行得非常充分.

数学抽象本质上是一个综合性的思维过程，所用到的主要是学生的形象思维和抽象思维，学生的形象思维能力一般来讲比较强，因此在数学情境中能够比较迅速地生成表象，这也就支撑了形象思维的展开. 相比较而言，数学抽象中的抽象思维能力培养则需要认真对待，抽象思维是人类思维达到高级阶段产生的一种能力，而抽象性是数学学科三大特征中最本质的特征之一，可以说没有抽象就没有数学，因此借助于数学抽象培养学生的抽象思维能力，利用抽象思维能力完成数学抽象，就是一个相互促进、相得益彰的过程.

站在思维能力的角度理解数学抽象，可以让数学抽象不至于在教学过程中变得空洞化，这是一个非常重要的思路，而这也意味着数学抽象的教学从经验走向了专业，其为数学学科核心素养的其他要素落地提供有益的思考与借鉴.