相同集聚因子时纤维悬浮液的流动特征及机理

陈婷婷，王晨,程金兰，朱文远，陈务平

(南京林业大学江苏省制浆造纸科学与技术重点实验室, 南京林业大学江苏省林业资源高效加工利用协同创新中心，南京 210037)

纤维悬浮液在管路中从层流发展为湍流的过程中会表现出几种不同的流动状态：在较低的流速下，纤维交织形成的网络结构在管路中像刚体一样柱塞流动，此时在壁面附近存在着很薄且呈层流状态的水环对柱塞起润滑作用；随着流速的增加，柱塞的直径不断减小，同时水环的厚度逐渐增加且呈湍流状态，最终柱塞被完全破坏，管路中的悬浮液处于完全的湍流状态[1]。

Xu等[2]的研究结果表明随着纤维浓度和雷诺数的变化，悬浮液速度分布曲线呈现出5种不同的变化，纤维和纤维絮团会降低悬浮液的湍流强度。Jäsberg[3]建立了柱塞阶段流速分布模型以及压力损失半经验公式。Lavenson等[4]得出预处理后的玉米秸秆悬浮液以及普通纤维悬浮液流动时平均屈服应力与流变仪得到的静态测量结果吻合较好。Nikbakht等[5]对3种不同长度植物纤维悬浮液的流动变化过程进行研究，认为柱塞的变化是流动摩擦阻力与柱塞自身强度相互作用的结果。Tozzi等[6]的研究结果表明当质量浓度达到一定值时，纤维悬浮液的流动才能满足使用广义牛顿流变模型所需要的均匀性要求，而不同长度的纤维满足均匀性要求所要达到的质量浓度也不同。

纤维浓度和尺寸是悬浮液流变性能[7-8]和流动状态变化[9-11]的重要影响因素。但由于所使用的不同尺寸的植物纤维性质及尺寸分布差异性较大，增加了实验结果的不确定性。采用性质相同并且尺寸均匀性较好的人造纤维代替复杂的植物纤维，可以在一定程度上排除上述干扰因素。集聚因子表示在悬浮液内以单根纤维长度为直径的球形区域内纤维的总数目，可以用来描述悬浮液内纤维的交织情况和絮聚的程度，能较好地反映悬浮液网络结构中纤维之间的相互作用以及勾连聚集的状态[12]。

以集聚因子作为试验条件可以在综合考虑浓度及纤维尺寸的前提下探讨纤维悬浮液流动状态的变化机理。笔者利用超声多普勒测速仪(ultrasonic doppler velocimeter, UDV)对4种相同牌号但不同尺寸的尼龙纤维悬浮液在试验管路中的流场进行测量，计算相同集聚因子条件下，纤维柱塞尺寸改变过程中的屈服应力，分析讨论了纤维悬浮液流动状态变化的原因，为进一步认识纤维悬浮液在实际应用过程中的流动特性提供理论依据。

1 材料与方法

1.1 试验材料

试验所使用悬浮液中液相为清水，固相分别为4种不同尺寸参数的尼龙66纤维，纤维密度约为1 100 kg/m3。悬浮液集聚因子的变化范围在70～100，其计算方法如式(1)所示：

(1)

式中：N为集聚因子；Cv为体积分数，%；A为纤维形状系数，是纤维长度与直径的比值。

纤维长度、直径、形状系数以及根据式(1)计算得到纤维占悬浮液的体积分数如表1所示。其中1#、2#、3#纤维具有相同的长度而直径不同，4#纤维的长度较短，但与2#纤维有相同的直径。悬浮液总体积控制在180 L，根据体积分数计算得到纤维体积，再由纤维密度计算并称取相应质量的纤维投入储罐内加水到规定体积。试验前，使用储罐内的搅拌器充分分散纤维，使其均匀分布。

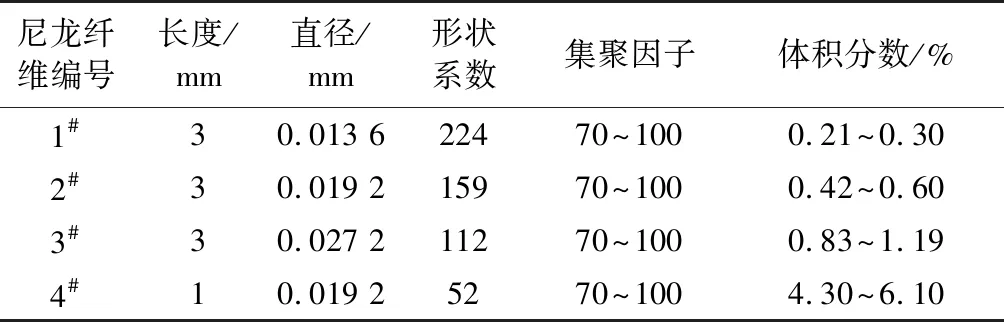
表1 尼龙纤维尺寸和纤维悬浮液体积分数Table 1 The nylon fibers’ sizes and the volume concentrations of suspensions

1.2 试验方法

试验管路系统如图1所示。纤维悬浮液储存在容积为220 L的储罐内，搅拌器在试验过程中保持储罐内的纤维均匀分布。悬浮液由变频离心泵泵送经循环管路返回储罐，离心泵的额定最大工作流量为60 m3/h。循环管路为透明聚氯乙烯(PVC)圆管，半径为25.4 mm，总长为14 m，其中测试范围为长度4.6 m的水平直管段。

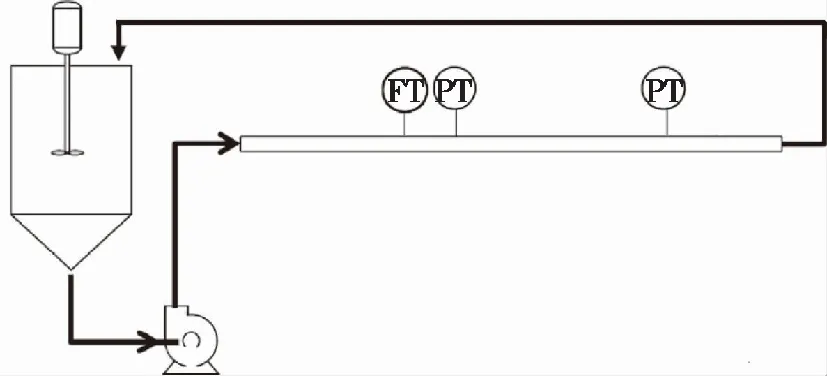
图1 试验装置示意图Fig. 1 Schematic of the experimental set up

管路中流量的测量采用FMG 606型电磁流量计(美国Omega公司)，精度为0.50%。悬浮液流经测试段的压力差由分别安装在测试段起点和终点的PX 409型压力传感器(美国Omega公司)的测量值计算得到，传感器的精度为0.05%。流量和压力数据使用USB 6501型数据采集器(美国NI公司)自动采集。

图2 尼龙纤维悬浮液柱塞半径的变化Fig. 2 The plug size of the nylon fiber suspension

悬浮液在管内流速分布采用DOP 3010型UDV(瑞士Signal Processing公司)测量，其工作原理为超声发射装置周期性地发出超声脉冲，接收装置收到在超声波路径内的目标所产生的反射波，通过检测流体中分散的固体颗粒的反射位移变化从而获得流体的速度[13]。试验中采用的超声波测量参数为发射频率4 MHz，探头直径5 mm，多普勒角度为78°。每个流速下进行300 s连续测量并取时均值。

柱塞半径的确定基于UDV的测量结果，利用MATLAB软件计算得到沿管路半径方向各位置的平均流速、应变率和湍流强度。分别以管路中心线这3个参数值为基准，找出0.99倍基准参数所对应的半径位置，再将由此3种方法确定的半径值取平均作为柱塞半径[5]。其中，平均流速为测量时长范围内的流速时均值；应变率为流速沿管路半径方向上的速度梯度；湍流强度由速度脉动的均方根值与平均流速的比值得到。由柱塞半径及压力损失，依据式(2)可以计算得到流动过程中柱塞屈服应力[4]:

(2)

式中：τy为柱塞屈服应力，Pa；l为测试段长度，m；Δp为测试段压力损失，Pa；rp为纤维柱塞半径，m。

纤维悬浮液在管路中流动时，柱塞的移动类似于刚性圆柱体的运动[3]。柱塞内部纤维由于相互间的勾连聚集作用而相对位移不大，可以认为不会出现柱塞内部纤维穿过外部纤维网络进入水环的现象，柱塞屈服应力应符合流变学测试结果。因此由式(3)所示尼龙纤维悬浮液屈服应力流变学试验结果[14]可以计算得到柱塞内的平均体积分数：

(3)

式中：τy为柱塞屈服应力，Pa；A为纤维形状系数；Cv为体积分数，%。

水环对柱塞的作用可以由式(4)所示柱塞边缘平均雷诺应力表示：

(4)

式中：τ为柱塞边缘平均雷诺应力，Pa；ρ为水的密度，kg/m3；u′为速度脉动，m/s。

2 结果与分析

2.1 柱塞半径及屈服应力的比较

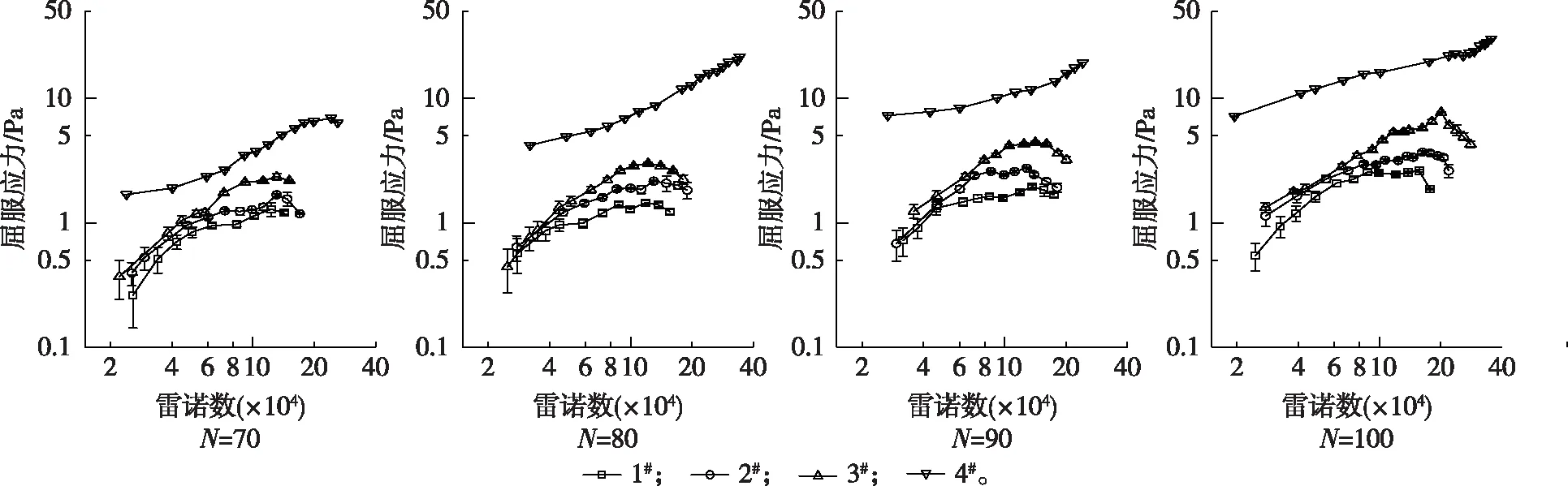
图3 尼龙纤维悬浮液屈服应力的变化Fig. 3 The yield stress of the nylon fiber suspension

4种尼龙纤维悬浮液的柱塞半径和屈服应力随雷诺数增加的变化过程如图2和图3所示。同一纤维随集聚因子的增大，其柱塞半径在相同雷诺数时也越大。在相同集聚因子时，同一雷诺数下形状系数越大的纤维柱塞半径越小，并且随着雷诺数的增大其柱塞半径减小的速度越快。使用流变仪对纤维悬浮液屈服应力测试结果表明，集聚因子的增大对于同一纤维而言意味着浓度的增加，纤维网络结构强度也随之增强，其屈服应力也增大。而相同集聚因子时，形状系数小的纤维悬浮液屈服应力反而较大[14]。这与图3流动过程中同一纤维随集聚因子变化以及不同纤维在相同集聚因子时其悬浮液在相同雷诺数下的屈服应力变化规律是相同的。屈服应力是纤维网络结构强度的流变学表现[15]。纤维悬浮液屈服应力越大，柱塞在受到流动阻力剪切作用时的影响也就越小。但是比较图2和图3也可以看出，柱塞半径都是单调减小的，而屈服应力除了4#纤维在集聚因子等于80，90和100时为单调递增，其余结果均呈现先增大后减小的趋势。这说明流动阻力的剪切作用对于柱塞纤维网络结构并不是单纯地破坏，纤维悬浮液流动状态变化的内在机理是较为复杂的。

2.2 流动状态变化的机理分析

根据屈服应力计算所得柱塞内平均体积分数随雷诺数变化如图4所示。可以看出，除了4#纤维在集聚因子分别为80，90和100时的数据结果一直上升以外，其余柱塞内尼龙纤维平均体积分数随着雷诺数的增加表现出先逐渐上升而后减小的趋势。这是因为纤维网络可以看成是具有一定压缩性的多孔介质，在剪切力的作用下，纤维网络结构会变得致密[16]。所以可以推断，柱塞的不断减小一方面是因为外部水环的湍流旋涡将柱塞表面的纤维不断剥离[3]，另一方面还存在着纤维网络在流动阻力的剪切作用下被不断压缩的过程。这导致了柱塞内部纤维平均体积分数的增加，纤维间勾连聚集的作用增强，从而表现为屈服应力的增大。将图3、图4与图2进行对比后发现，当柱塞半径与管路半径之比约为0.2时，柱塞内部平均体积分数和屈服应力出现最大值，而后逐渐减小。可能的原因在于此时大量的纤维已从柱塞脱离进入水环，并且湍流旋涡的强度和旋涡尺度已能够影响到柱塞内部，进入了对柱塞的侵蚀阶段[5]，导致了柱塞中纤维浓度下降，屈服应力也随之减小，并最终被完全破坏，悬浮液进入完全湍流状态。集聚因子为80，90和100的4#纤维悬浮液柱塞内体积分数单调递增，则说明在所测试的雷诺数范围内，它们仍处在压缩阶段，还未进入侵蚀阶段，因此屈服应力表现为单调递增。

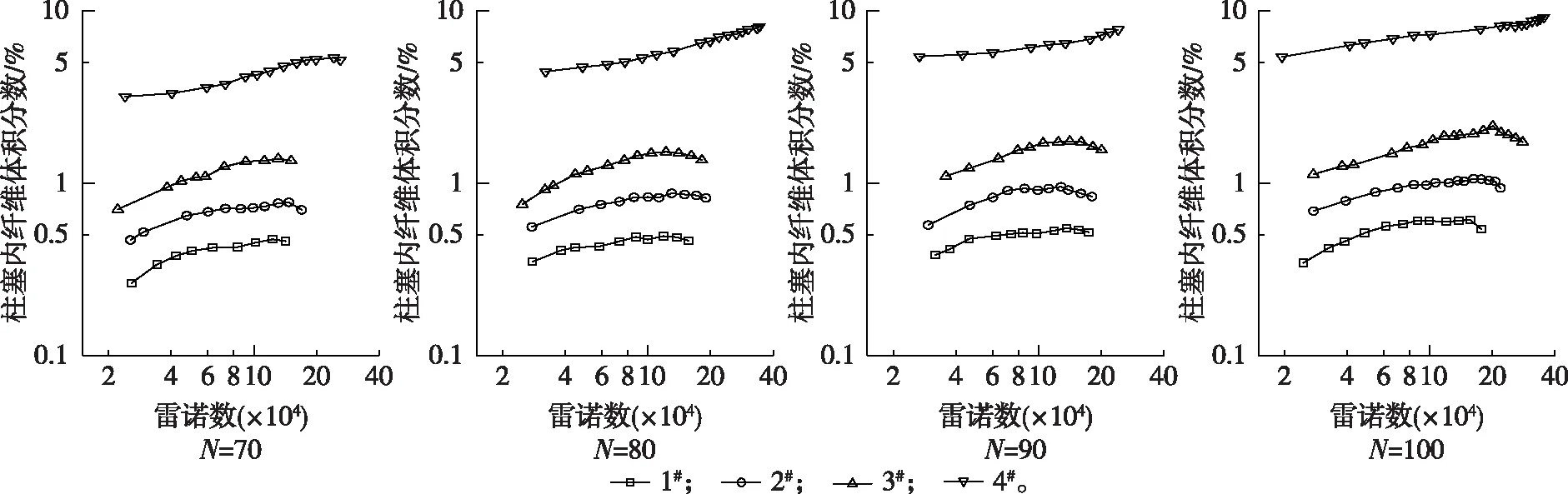
图4 柱塞内部平均体积分数的变化Fig. 4 The average concentration of volume percent in the plug

柱塞边缘平均雷诺应力与屈服应力的比值随雷诺数的变化如图5所示。由图5可以看出，随着雷诺数的不断增加，平均雷诺应力与屈服应力的比值也逐渐增大。这说明流速变化时，平均雷诺应力增加速率要高于屈服应力。而相同集聚因子时，形状系数较小的尼龙纤维悬浮液在同一雷诺数时其平均雷诺应力与屈服应力的比值也较小。这是因为形状系数较小的尼龙纤维悬浮液的屈服应力较大，而其柱塞边缘平均雷诺应力较小(图6)所造成的。图6同时还表明柱塞能够影响水环的湍流，柱塞的半径越大，对水环湍流程度的抑制作用越强。

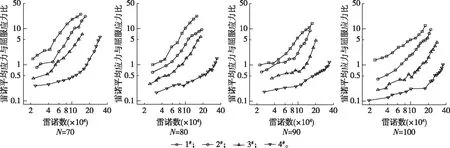
图5 柱塞边缘平均雷诺应力与屈服应力的比值Fig. 5 The ratio of average Reynolds stress at the edge of the plug to the yield stress

此外，从图5可以看出，在所测试的雷诺数范围内，集聚因子为80～100的4#纤维悬浮液，其平均雷诺应力与屈服应力的比值基本都小于或略大于1。而其余纤维悬浮液屈服应力和柱塞内体积分数变化趋势出现“拐点”时所对应的平均雷诺应力均数倍甚至十几倍于屈服应力。说明只有当湍流强度明显高于纤维网络结构强度时，柱塞才能进入侵蚀阶段。

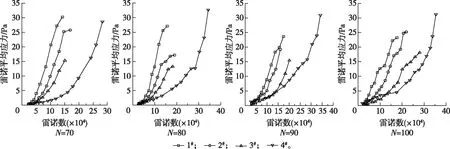
图6 柱塞边缘平均雷诺应力Fig. 6 The average Reynolds stress at the edge of the plug

3 结 论

利用超声多普勒测速仪测量得到了相同集聚因子时4种不同尺寸尼龙纤维悬浮液在圆管中流动时的柱塞尺寸，计算获得了屈服应力随雷诺数变化的过程，并分析了流动状态变化的内在机理，得出以下结论：

1)尼龙纤维悬浮液柱塞半径随着雷诺数的增大而不断减小，不仅是由于水环的湍流作用使得其表面纤维被剥离，还因为柱塞纤维网络受到流动阻力的压缩作用而变得致密。这导致了雷诺数增加的初始阶段，柱塞内部纤维平均体积分数的增加，并表现为屈服应力的不断增大。

2)流速变化时，平均雷诺应力增加速率要高于屈服应力。当柱塞半径与管路半径之比小于0.2时，湍流强度明显高于纤维网络的结构强度，水环的湍流效应与旋涡尺度影响到了柱塞内部，柱塞变化进入被侵蚀阶段。此时柱塞内纤维平均体积分数开始下降，屈服应力逐渐减小，柱塞内纤维网络开始崩溃，并最终被完全破坏。

3)在相同集聚因子时，形状系数较小的尼龙纤维悬浮液在同一雷诺数时具有更大半径的柱塞，其屈服应力也相对较大。柱塞同样会对水环的湍流程度产生影响，表现为柱塞半径越大，对水环湍流程度的抑制作用越强。