线控制动系统车辆制动与横摆稳定性协调控制

(青岛理工大学 机械与汽车工程学院，山东 青岛 266000)

线控机械制动系统(EMB)采用电子机械系统取代传统制动系统中的液压部件，是未来制动系统的主要形式[1]。随着电动汽车技术的不断发展，其制动稳定性控制问题引起了国内外学者的持续关注，但许多研究倾向于装有传统液压制动系统或装有线控液压制动系统(EHB)的车辆[2-3]，对装有EMB车辆的制动与横摆稳定性协调控制研究较少。

在装有EMB的车辆纵向制动控制方面，文献[4]中针对电动汽车防抱死制动系统轮毂电机制动力控制问题，提出一种改进线性二次型最优控制方法且据此设计防抱死控制器，在不同附着路面上进行紧急制动，仿真验证了该策略能够提高制动系统的控制精度和响应速度。文献[5]中针对EMB的不确定和非线性问题，建立EMB系统系统及1/2车辆动力学模型，提出一种基于滑移率的模糊滑模控制算法。上述研究只进行了纵向制动性能的研究和测试，未考虑车辆横、纵向耦合控制问题。

在车辆行驶过程中车身稳定性控制方面，文献[6]中针对带有线控制动系统的车辆进行研究，提出一种横摆稳定性优化控制策略，采用比例积分(PI)控制算法求出维持车辆稳定所需的横摆力矩，结合广义逆法和数学规划法，将所需横摆力矩分配到作用车轮上。文献[7-8]中针对分布式电动汽车稳定性控制问题，通过滑模控制器计算附加横摆力矩，并采用二次规划的方法分配各个车轮所需的纵向力，同时优先基于轮毂电机输出驱动、制动力来实现横摆力矩分配，通过加速、减速及双移线仿真分析验证了该策略的有效性。文献[9]中针对车辆弯道制动过程中的稳定性控制问题，提出了一种模糊比例-积分-微分(PID)控制算法，依据横摆角速度和质心侧偏角的期望值与实际值之间的偏差输出各个车轮的滑移率。

文献[10]中针对分布式驱动电动汽车复合制动系统转矩分配问题，采用加权最小二乘控制对四轮液压制动转矩和电机制动转矩进行分配，并通过有效集算法求解目标函数，以期达到保证车辆稳定性的同时最大限度地回收制动能量。为了提高车辆乘坐舒适性和行驶稳定性，文献[11]中应用基于视觉的转向和制动动力学协调控制系统，基于反步控制器设计技术设计了等效控制律和模糊自适应滑模趋近律并实车测试验证策略的有效性。

上述研究大多仅单独进行车辆稳定性研究或是对装有传统液压制动系统、EHB的车辆进行研究，对于装有EMB的车辆制动与横摆稳定性协调控制的研究较少，因此，本文中针对装有EMB的车辆制动与横摆稳定性协调控制问题进行研究，设计分层控制结构，顶层控制器运用滑模变结构控制和模糊控制理论确定纵向目标制动力及横向目标横摆力矩；底层控制器采用二次规划方法，充分考虑弯道制动过程中的车身载荷偏移及轮胎物理极限问题，以轮胎利用率为目标函数，采用有效集算法求解目标优化函数，主要解决车辆制动目标纵向力与横摆力矩分配问题，从而达到满足车辆在制动时横纵向协调最优控制的目的。

1 车辆动力学建模

1.1 整车动力学建模

图1为本文中设计的车辆制动协调控制策略框图。选取装有EMB的乘用车进行制动与横摆稳定性协调控制研究，忽略空气阻力，主要考虑车辆纵向、横向、横摆及4个车轮的旋转自由度，按照达朗贝尔-拉格朗日定理建立7自由度整车动力学模型[12]。

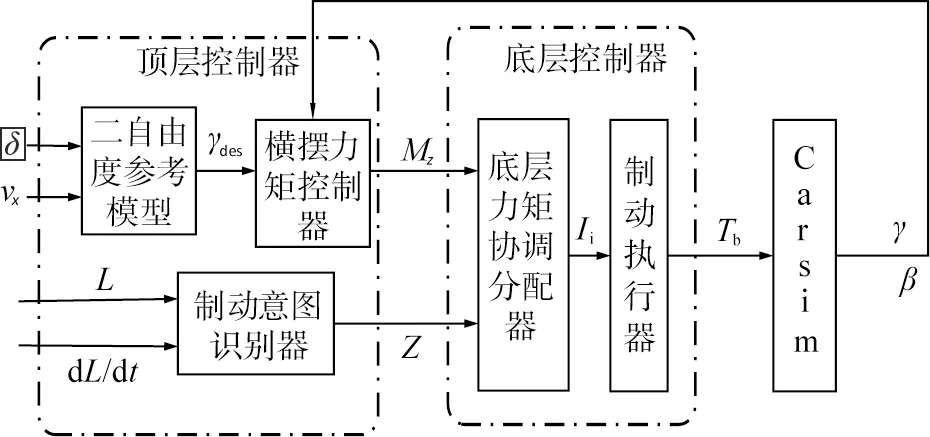
□δ 为前轮转角;vx为车辆纵向形式速度;γdes为理想横摆角速度;Mz为目标横摆力矩;Ii为驱动电机电流;Tb为制动力矩;γ为车辆实际横摆角速度;β为车辆实际质心侧偏角;Z为制动强度;L为制动踏板开度。图1 车辆制动协调控制策略框图

车辆纵向运动方程为

(1)

车辆横向运动方程为

(2)

车辆横摆运动方程为

b(Fy3+Fy4)+Mz，

(3)

(4)

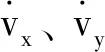
(5)

(6)

1.2 线控机械制动模型

选用浮动钳盘式EMB制动执行器，其模型包含电机模型、行星减速机构模型、滚丝杠模型及制动器模型。制动器制动力矩Tbi[13]可表示为

Tbi=kbi(ktiIi-Tfi)，

(7)

(8)

式中：Tfi为驱动电机摩擦力矩；Ii为驱动电机电枢电流；kbi为车辆制动器的输出力矩系数；kti为车轮制动器的电机力矩系数；μbi为车轮制动器制动垫块摩擦系数；rbi为制动盘有效半径；ηsi为滚珠丝杠的机械效率；ixi为行星齿轮传动比；ηxi为行星齿轮机构的机械效率；phi为丝杠导程。

1.3 其他相关模型

在制动或转向的过程中，车辆会产生纵向和横向载荷转移，即4个车轮的载荷会发生相应的变化。本文中使用魔术公式轮胎模型估算4个车轮的纵向及横向制动力，具体细节见文献[14]；同时建立轮胎载荷估算模型，具体细节见文献[15]。

2 顶层控制器

为了达到最优的车辆控制性能，顶层控制器需要实时准确地完成横摆力矩的计算及制动意图的识别工作。本文中通过线性二自由度车辆模型计算出理想横摆角速度和质心侧偏角，运用滑模控制理论设计了横摆力矩控制律，同时制动意图识别器识别出制动意图及对应的制动强度，即完成对纵向制动力需求的求取。

2.1 参考模型

采用经典的线性二自由度车辆模型作为车辆稳定性参考模型，为了更好地评判车辆在制动过程中能否保持良好的稳定性，选取车辆横摆角速度和质心侧偏角为评价指标。

二自由度车辆运动微分方程为

(9)

式中：k1、k2分别为前、后轴等效侧偏刚度，N/rad，取值均为负；β为车辆的质心侧偏角，rad。当车辆处于稳态时，可以推导出车辆期望横摆角速度γd为

(10)

式中K为稳定性因数，

当车辆的横摆角速度较大，且路面不能提供足够的附着力时，上述理想横摆角速度并不能保证车辆安全性，需修正理想横摆角速度γd为

(11)

式中μ为实时路面附着系数。

同理，根据式(9)也可推导出理想质心侧偏角βd为

(12)

2.2 横摆力矩控制器

由于滑模控制理论具有响应迅速、鲁棒性强的特点，因此采用该理论设计横摆力矩控制器。本文中选择同时考虑横摆角速度与质心侧偏角[16]，因此定义滑模面为

s=γ-γd+ζ(β-βd)，

(13)

则有

(14)

式中ζ为权重因子。联立式(3)、(4)、(14)可以得出

(15)

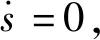
Mzeq=-a(Fy1+Fy2)cosδ+b(Fy3+Fy4)+

(16)

滑模控制的效果优劣取决于对滑模面及趋近率的选择，本文中选用改进的指数趋近率

Mzs=-K1|s|sgn(s)-K2s，

(17)

式中K1>0、K2>0，均为可变参数。

综上，本文的滑模横摆力矩控制器为

ΔMz=Mzeq+Mzs。

(18)

2.3 制动意图识别器

为了达到最优的控制效果，提高车辆控制系统控制精度，充分考虑人、车、路对控制系统的影响，采用模糊控制理论建立驾驶人制动意图识别器[17]，其利用路面、制动踏板开度L及其变化率作为制动意图识别器的输入，实时输出驾驶人制动意图及其相对应的制动强度，以此完成对于驾驶员真实制动意图的表征。图2为制动意图识别器模型。

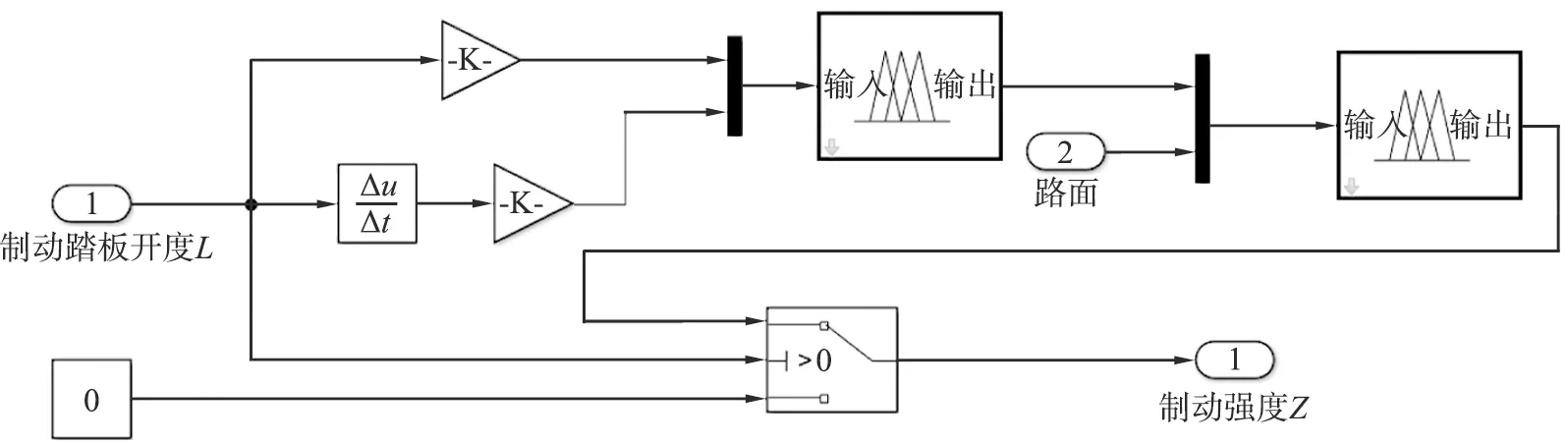
图2 制动意图识别器模型

3 底层控制器

底层控制器主要解决控制分配问题，即解决如何分配过驱动系统中的广义合力的问题。通过求解控制目标的优化问题，达到控制系统最优分配目的。控制分配问题可以描述为

Bu=v，

(19)

式中：B为控制效率矩阵；u为控制变量；v为广义合力。

3.1 优化目标的选取

为了合理高效地分配作用在4个车轮上的力矩，期望以此可以提高车辆的整体性能，一般采用轮胎利用率或轮胎耗散功率作为优化目标[8，18]，考虑到侧向力及侧向速度受实际条件限制，本文中采用轮胎利用率作为优化目标。简化侧向力后，得到定义轮胎利用率，为

(20)

因此选取优化目标函数为

(21)

整理得到矩阵形式表达为

(22)

式中Wu是u的权重矩阵，表征了u中各元素的约束关系。

3.2 协调分配控制算法

针对上述优化目标，本文中运用二次规划方法进行计算求解。为了较优地处理约束条件，缩短计算时间，首先将式(21)转化为序列最小二乘问题，然后通过引入权重因子，将该问题转化为加权最小二乘问题。

(23)

式中：uL、uH为控制变量u的上、下限，其取值受到路面附着系数及轮胎载荷的耦合影响；Wv为广义合力权重矩阵，且是非奇异矩阵，表征2个广义合力之间的权重关系。

3.3 有效集算法

针对上述加权最小二乘问题的求解，理论上需要汽车电子控制单元(ECU)实时高效地求解出最优值。有效集算法[19]是通过求解等式约束方程来完成控制分配的，它将每一次迭代中的部分不等约束当作等式约束求解，忽略其他的不等式约束，在有限次迭代中寻找出最优解，因此可以高效地解决本文中的加权最小二乘问题。

式(22)可以转换为如下形式：

(24)

依据优化目标函数的选取，确定本文中的控制变量u、广义合力v、控制效率矩阵B及影响u各元素之间的权重矩阵Wu，分别为

u=[Fx1,Fx2,Fx3,Fx4]T,

(25)

v=[Mz,mgZ]T,

(26)

(27)

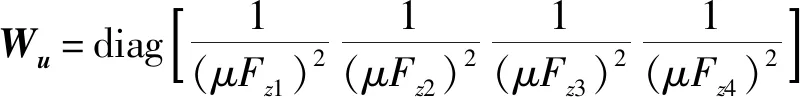
(28)

4 仿真分析

MATLAB/Simulink软件适用于控制系统运行性能的仿真研究,Carsim是专门针对车辆动力学的仿真软件，本文中采用Simulink与Carsim进行联合仿真,首先在Simulink中分别建立制动意图识别器模型、车辆模型、轮胎模型、线控制动系统模型及控制器模型，然后在Carsim中选择D-class sedan作为研究对象，建立Carsim整车模型，选择在对开路面上进行改变制动意图的工况仿真研究，联合仿真参数见表1。

4.1 对开路面上改变制动意图工况

为了验证在对开路面上该协调控制策略的控制效果，将对开路面的路面附着系数分别设置为0.4、0.85，其中左侧车轮对应路面附着系数为0.4，右侧车轮对应路面附着系数为0.85。车辆制动时的初始车速为80 km/h,2 s后驾驶员制动意图由轻度制动转为中度制动，车速低于15 km/h时结束仿真，仿真结果如图3—6所示。

表1 联合仿真参数

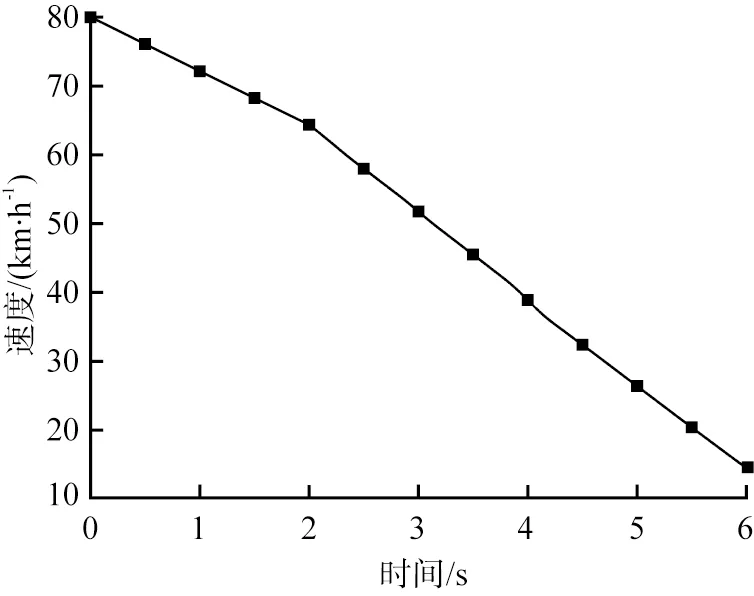
图3 车辆纵向速度仿真结果

图4 车辆制动力矩仿真结果

图5 车辆横摆角速度仿真结果

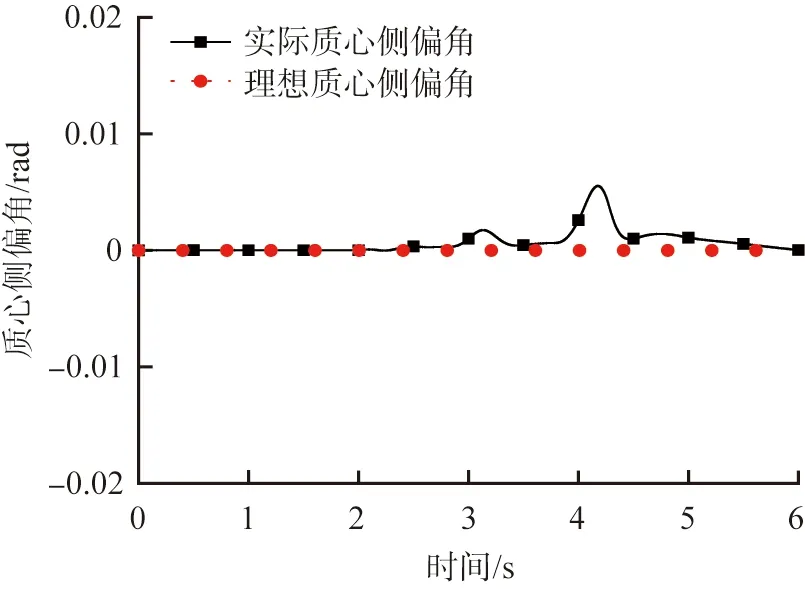
图6 车辆质心侧偏角仿真结果

4.2 仿真结果分析

由图3—6可知：当驾驶员制动意图为轻度制动时，车辆在对开路面上的车速不断下降，可以满足车辆纵向制动需求，且车辆的横摆角速度和质心侧偏角都保持在理想状态；经过2 s后，当制动意图由轻度制动转变为中度制动时，车速在不断下降且减速度比轻度制动时更大，同时车辆的横摆角速度出现细微波动，而后逐渐趋于稳定状态，且其最大值为0.02 rad/s，充分显示出了良好的制动稳定性，车辆的实际质心侧偏角与理想质心侧偏角基本相吻合，达到了理想的控制状态。仿真结果验证了该协调控制策略的有效性，其不仅可以满足纵向制动需求，同时最大限度地保证了横摆稳定性。

5 结语

本文中针对线控机械制动系统的车辆提出一种兼顾制动效能与横摆稳定性协调控制的车辆制动力分配策略，采用分层控制结构，运动用滑模控制理论及模糊控制理论设计了顶层控制器，运用二次规划优化理论设计了底层控制器，其中采用有效集算法完成对控制分配目标函数的实时求解工作。

通过MATLAB/Simulink与Carsim软件在对开路面上进行了转换制动意图的仿真研究，结果表明，该协调控制策略不仅可以满足车辆纵向制动需求，同时在保证制动效能的前提下还达到了车辆横摆稳定性控制要求，对解决线控制动系统车辆驱、制动转矩分配问题具有指导性意义。