变径流化床反应器内的气固流动特性数值模拟

(新疆大学 a. 化学化工学院，b. 煤炭清洁转化与化工过程自治区重点实验室，新疆 乌鲁木齐 830046)

流化床反应器因对固体物料的适应范围宽，固体之间的混合效果好、传热好，能够连续操作等优点被广泛应用于甲烷化、有机硅合成、污水处理、脱硫等领域[1-5]。由于流化床自身的特性，在反应过程中要不断加入物料，因此流化床内的颗粒流动存在不同程度的不稳定性。不同颗粒在流化床内的流动特征是不同的，随着表观气速的变化，流化床内的颗粒流动规律也会随之改变，出现混合、分离、聚集等现象[6-8]，因此，对流化床内颗粒流动行为进行研究是十分有必要的。

为了对流化床的气固流动特性进行深入的研究，补充实验存在的不足，并为实验和实际生产提供预测，数值模拟方法已经不可或缺[9-11]。目前常用的数值模拟的数学模型主要有欧拉-欧拉模型和欧拉-拉格朗日模型2种。前者忽略了颗粒间的相互作用，将颗粒当作连续性的介质，导致无法从颗粒尺寸层面对流化床进行分析。欧拉-拉格朗日模型(即计算颗粒流体力学(CPFD)模型)提出了颗粒群的概念，能够实现不同颗粒粒径的全分布，从而能更好地对流化床反应器的气固流动特性进行深入研究。目前已经有学者采用CPFD方法对流化床进行研究并证明其可行性[12-13]。Shi等[14]基于CPFD方法研究了颗粒粒径分布对循环流化床立管中气固流动及颗粒返混的影响，结果表明该方法能够模拟循环流化床立管中气固流动特性。Fotovat等[15]采用CPFD模型对生物质-石英砂气泡流化床进行模拟，再现了流化床内气泡大小及气泡速度分布不对称的特征。

针对流化床的模拟研究，大部分文献都是从流化床下部加入循环物料。本文中所研究的流化床反应器不仅是变径的，而且固体物料进料方式也不同于其他的流化床，是在流化床的扩大段由螺旋加料器不断将物料送入反应器。作为一个新型的流化床反应器，本文中基于CPFD方法建立了流化床的三维模型，在不同气速和初始物料量下，对流化床反应器内的气固流动特性及流化床颗粒壁面聚集现象进行研究，研究结果可为工业生产提供一定的参考。

1 模型及模拟条件

1.1 几何模型

本文所用流化床反应器模型是根据新疆某企业提供的数据所建，数值模拟过程中的所用的流化床反应器几何结构及三维模型如图1所示。反应器直径D1为160 mm，总高度H为2 733 mm，主要由反应段、过渡段、扩大段3个部分组成。顶部有颗粒出口，反应完的物料从反应器的底部出口排出。在反应器中上部，有加料器不断将物料输送到反应器中。受计算机计算能力的限制，模拟时将螺旋进料简化为中间进料。进料口直径为50 mm，上部固体及气体的出口直径为40 mm。模拟采用颗粒与企业所给物料参数一致。

1.2 数学模型

本文中采用的CPFD方法，本质上是基于颗粒计算单元多相流(MP-PIC)方式的数值模拟方法，该方法能够在三维空间内将颗粒相和流体相耦合[16]。其数学方程如下。

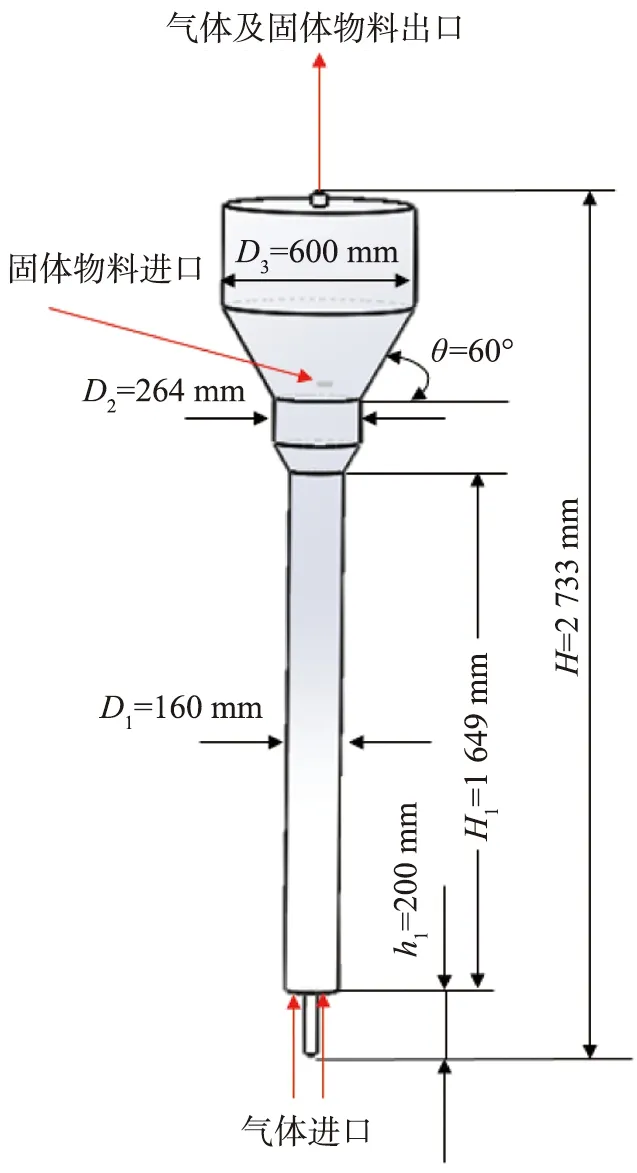
图1 流化床几何模型

1)流体相方程。两相流中气体连续性方程[17]为

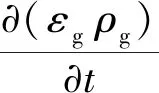
(1)

式中：εg为气体相体积分数；ρg为气相密度，kg/m3；ug为气相速度(气速)，m/s。

气相的动量方程为

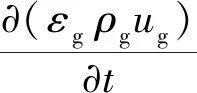
εgρgg-F，

(2)

式中：p为压力，Pa；τg为气体应力张量；g为重力加速度，m/s2；F为颗粒与气体间的动量交换率。

气固动量交换率F的计算公式为

(3)

式中：f为颗粒概率函数；up为颗粒速度，m/s；Dp为曳力系数；mp为颗粒质量，kg；ρp为颗粒密度，kg/m3。

2)颗粒相方程。颗粒间的动量方程[18]为

(4)

式中：rp为颗粒半径，m；εp为颗粒相体积分数。

颗粒间相互碰撞作用力可以利用颗粒正向作用力τp来描述，即

(5)

式中：ps为压力常数，Pa；ε为常数，取值为10-7；εcp为颗粒紧密堆积时的体积分数；β为常数，推荐值为2～5。

3)气固曳力模型。本文中采用的是Wen-Yu模型，其相间曳力系数Dp计算公式为

(6)

式中：μg为气体的动力黏度，Pa·s；fb为常数。

1.3 模拟条件

模拟的对象为整个流化床的循环过程，模拟参数如表1所示。在计算开始时，流化床反应器内有一定高度的物料。在流化床的底部通入空气，进料口也有物料不断加入。颗粒在气体的作用下分别通过流化床反应器的反应段、过渡段以及扩大段，少部分颗粒从上部出口排出。由于在实际生产中希望更多的颗粒停留在流化床的反应段，因此需对不同流化风速进行探究，为企业生产提供参考。

表1 流化床循环过程模拟参数及操作条件

1.4 网格无关性验证

本文中研究的流化床模型尺寸为直径160 mm、高度2 733 mm。在进行模拟计算时考虑到网格流化床的出口管道、底部排渣管道较之整体模型较为细小，需对其进行网格细化，网格细化后的模型如图2所示。本文中分别划分了3种网格，即网格1、网格2和网格3,网格信息如表2所示。

设气速为1 m/s，初始物料高度为500 mm，分别提取了3种不同网格模型在同一位置的颗粒体积分数沿流化床高度的变化，如图3所示。网格2与网格3的模拟结果基本一致，由于网格数越多，所需要的计算资源就越多，而使用粗糙网格又会导致模拟过程中信息缺失，使得模拟结果不准确，因此综合考虑本文中数值模拟采用的网格模型为网格2。

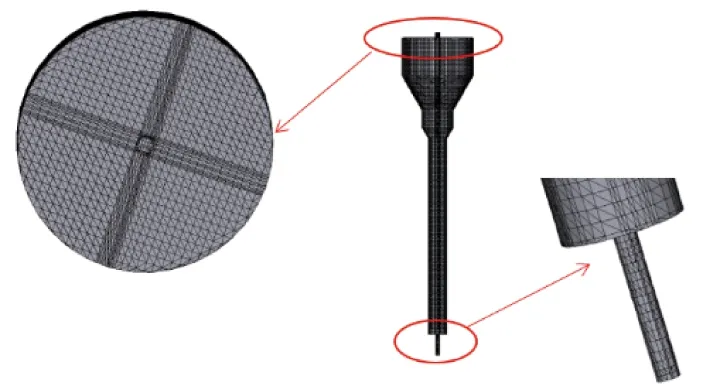
图2 计算网格划分

表2 3种计算网格信息

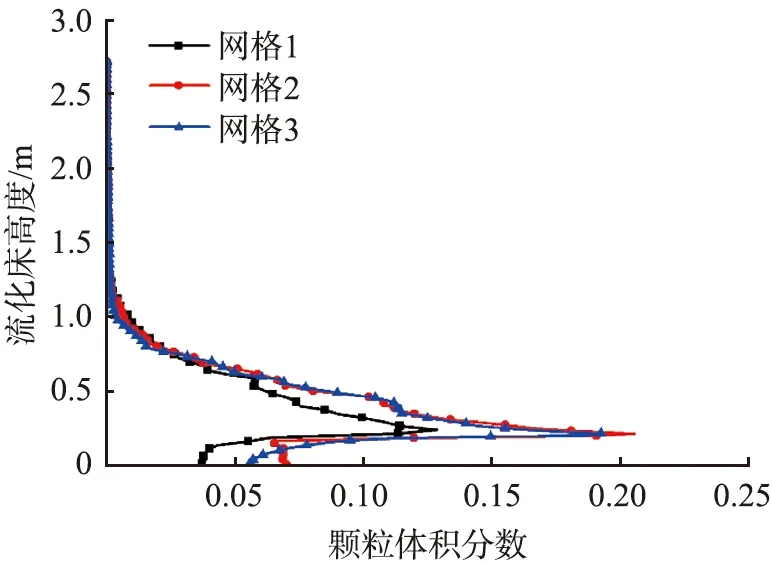
图3 不同网格尺寸下流化床内轴向颗粒体积分数分布

2 结果分析

2.1 气速对颗粒体积分数分布的影响

图4给出了不同气速下、初始物料高度为400 mm时，流化床内轴向颗粒体积分数分布。在流化床的底部，由于颗粒之间的相互作用以及碰撞，使得颗粒的速度很难在短时间内快速增加，从而使得颗粒大部分在流化床的底部聚积。颗粒体积分数为底部大、上部小的分布，从图像的走势上看近似于指数分布。随着气速的增加，流化床底部的颗粒体积分数由0.25减小到0.13左右，颗粒所占体积明显减小。当气速不小于2.5 m/s时，流化床反应器反应段的颗粒体积分数都增大至0.025，即在流化床反应器反应段的中、上部颗粒所占体积明显增大。这是因为，随着气速的增加，颗粒随着气体快速通过流化床，颗粒在床内的停留时间缩短,所以流化床底部的颗粒体积分数随之减小。与气速较小时相比，整个流化床内的颗粒体积分数均增大。

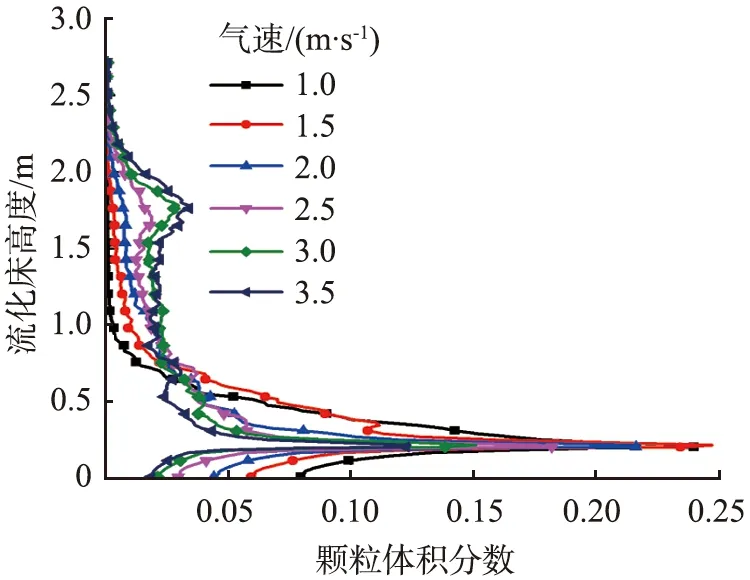
图4 气速对流化床内轴向颗粒体积分数的影响

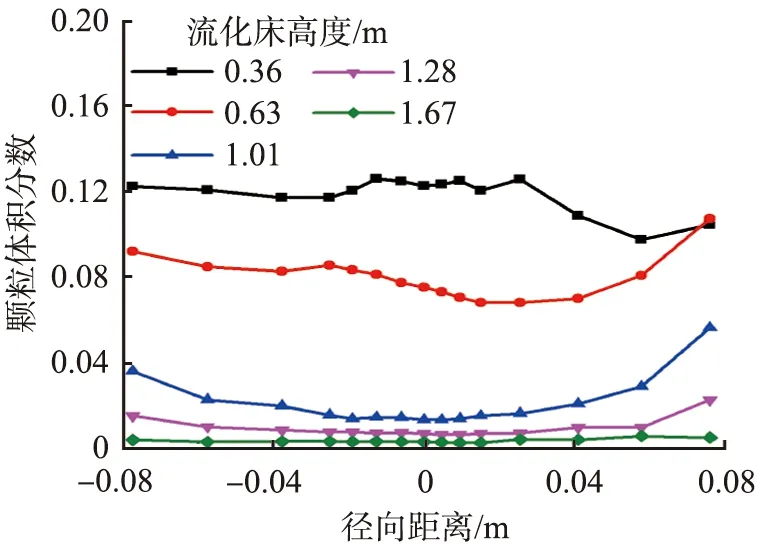
图5为初始物料高度为500 mm时，不同气速下流化床内不同高度截面上颗粒体积分数的径向分布。随着气速的增加，在流化床内的同一高度的径向颗粒体积分数逐渐减小。当流化床高度H>0.63 m时，径向颗粒体积分数随着气速的增大而增加。随着气速的增大，有更多的颗粒随着气体进入了流化床反应段的上部，从而减少了流化床底部的颗粒堆积。颗粒体积分数的径向分布呈中间小、两边大的“U”形分布，越靠近壁面，颗粒聚集越多。由于下降的颗粒与上升的颗粒在近壁面区域发生碰撞，沿壁面往下降落，出现返混，因此壁面附近颗粒体积分数呈增大的趋势。

2.2 气速对颗粒聚集的影响

设气速为2 m/s，初始物料高度为400 mm，流化床内不同高度截面颗粒速度径向分布如图6所示。由图可以看出，颗粒径向速度呈倒“U”形分布，即两边低、中间高。随着流化床高度的增加，流化床内的颗粒径向速度逐渐增大。颗粒速度为正值时表明颗粒在沿流化床上升，颗粒速度为负值时表明颗粒向流化床底部回流。随着流化床高度的增加，气体速度呈增大趋势，且中心的气体速度较大，如图7所示，因此在流化床中心的携带的颗粒也较多，颗粒速度也较大，而在靠近壁面附近颗粒速度较小。在靠近有加料口的一侧，颗粒在壁面附近的上升速度与中心处相比较小，更多的颗粒向流化床底部回流，从而促使更多的颗粒在壁面附近聚集(见图8)。当气速较小时，颗粒大部分聚集在流化床的底部；当气速增大后，颗粒的分布更为均匀。随着气速和流化床高度的增加，颗粒在壁面的聚集行为更为明显。当流化床高度H不小于1.53 m时，颗粒速度明显减小，原因是流化床由反应段进入了过渡段，流化床的结构发生了变化，导致径向颗粒体积分数减小。

(a)气速为1.5 m/s

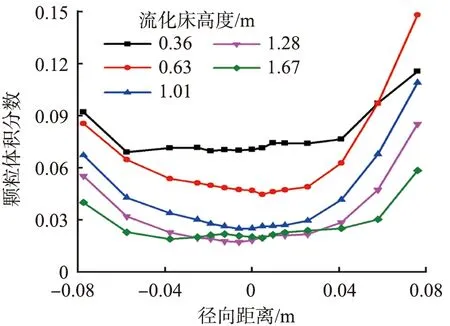
(b)气速为2.5 m/s图5 不同气速下流化床内不同高度截面颗粒体积分数径向分布

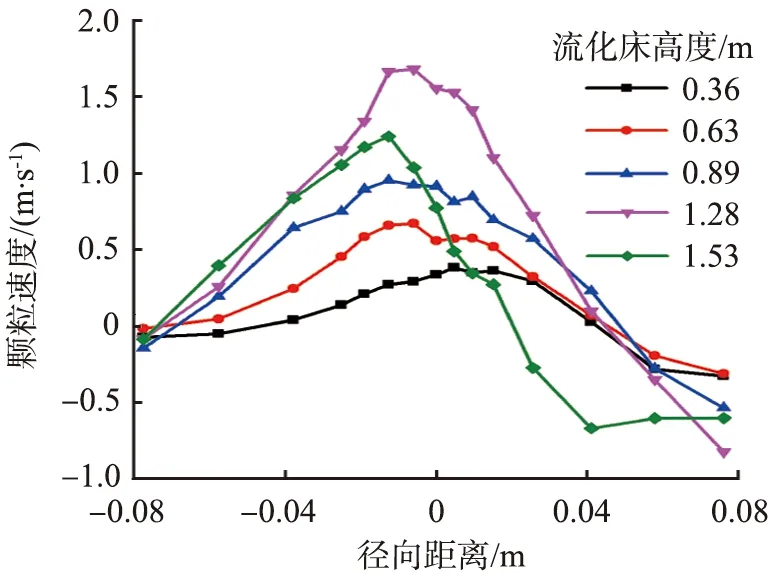
图6 流化床内不同高度截面颗粒速度径向分布

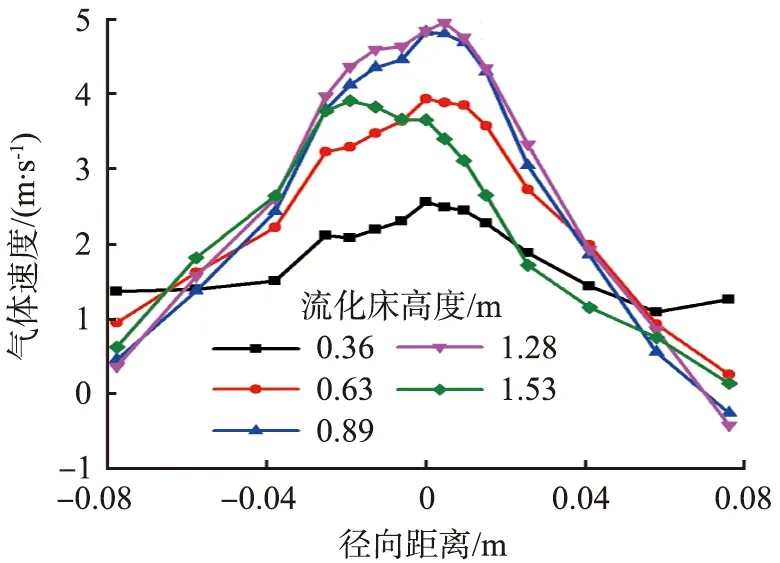
图7 流化床内不同高度截面气体速度径向分布

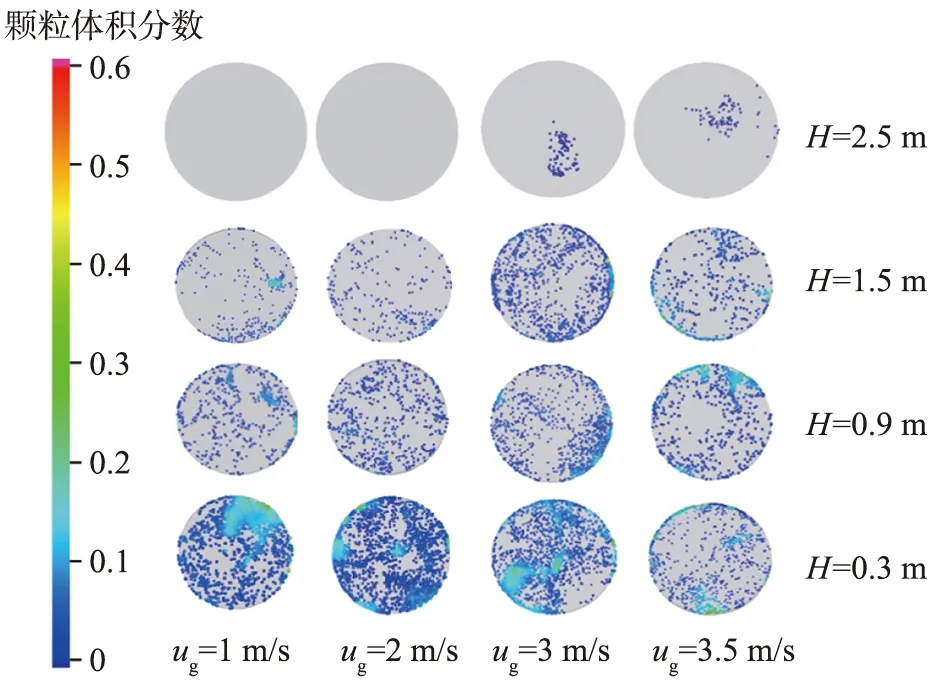
H—流化床高度;ug—气速。图8 流化床内不同高度截面颗粒分布云图

2.3 颗粒停留时间分布

颗粒停留时间作为一个体现流化床反应器内颗粒混合程度以及颗粒流动特性的参数，对其进行研究是十分必要的。流化床内不同高度截面颗粒停留时间瞬态分布如图9所示。为了更加清晰地看到图中的颗粒，后处理时将颗粒全部放大了6倍。不同颗粒颜色表示不同颗粒的瞬态停留时间，蓝色表示颗粒在流化床的该截面停留时间较短，红色表示颗粒在流化床的该截面上停留时间较长。当H<0.6 m时，颗粒在流化床的底部具有较宽的颗粒停留时间分布。这是因为，在流化床底部颗粒体积分数较大，上升的颗粒与下降的颗粒在此处碰撞较为激烈，从而增大了颗粒之间的返混程度，所以颗粒在流化床底部停留时间分布较宽。

由图9可知，在流化床的同一高度截面上，颗粒停留时间各不相同。颗粒在流化床的中心处的停留时间较短，在壁面处的停留时间较长。由前文可知，颗粒在流化床中心位置的速度较大，颗粒体积分数较小，颗粒在流化床反应器中心发生碰撞返混的概率也小，因此返混程度小，颗粒停留时间也短。而在壁面附近颗粒速度较小，颗粒沿壁面下落的概率更大，从而增大了颗粒之间的相互碰撞与返混机会，因此壁面附近颗粒停留时间较之流化床中心处长，导致颗粒在壁面附近更加容易聚集。聚集的颗粒不断变多，使得其下降的速度变大，更加容易产生返混[19]。

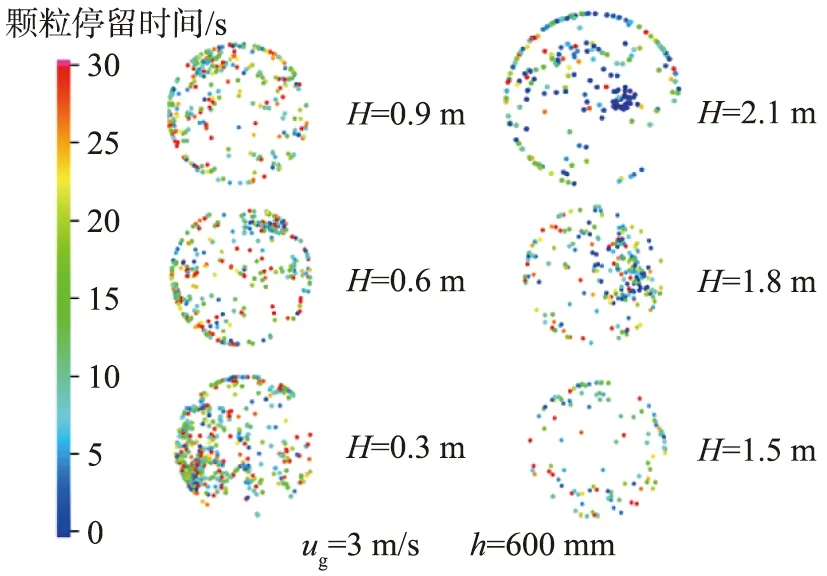
H—流化床高度;h—初始物料高度;ug—气速。图9 流化床内不同高度截面上颗粒停留时间瞬态分布

2.4 初始物料量对颗粒体积分数分布的影响

流化床内初始物料量的多少是影响流化床的气固流动特性的一个重要因素。图10给出了气速为2.5 m/s时，不同初始物料量条件下流化床内同一位置的轴向颗粒体积分数分布。随着初始物料高度的增加，颗粒体积分数沿着流化床床高的分布呈增大趋势。随着初始物料高度从300 mm增加至800 mm，流化床底部的颗粒体积分数也从0.15增大到0.34。在流化床的反应段颗粒体积分数最大可达到0.10。

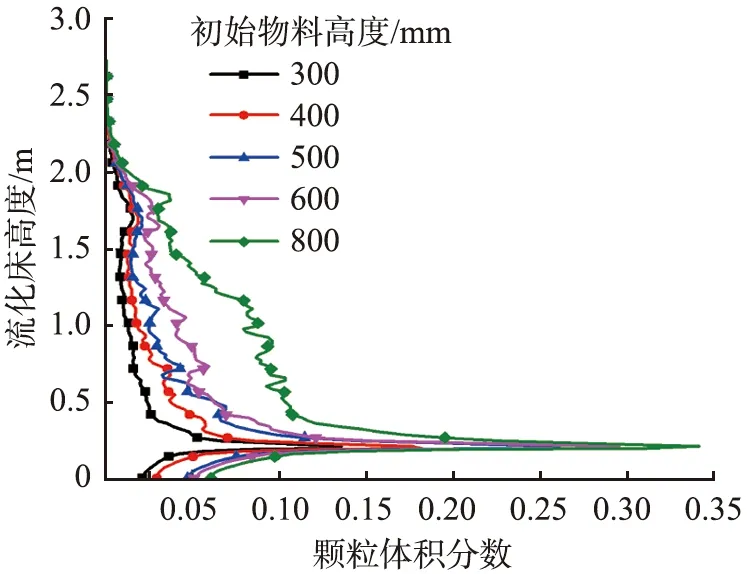
图10 初始物料量对流化床内轴向颗粒体积分数分布的影响

不同初始物料高度h下流化床内颗粒体积分数径向分布如图11所示。随着初始物料高度的增加，同一位置的径向颗粒体积分数增大，颗粒体积分数由0.02增大至0.087，增加了3倍。初始物料高度为600 mm、气速为2.5 m/s时，不同高度截面的径向颗粒体积分数分布如图12所示。由图可以看出，径向颗粒体积分数随着流化床轴向高度增加呈减小趋势。当床高H<1.67 m时，不同高度径向颗粒体积分数的分布比较集中，说明大部分的颗粒都集中在流化床的反应段，有利于后续反应的进行。当床高H>1.67 m以后，径向颗粒体积分数开始减小，表明颗粒由流化床的反应段进入过渡段，直径突然变大，颗粒速度变小，颗粒向流化床底部回流，因此颗粒体积分数呈减小的趋势。

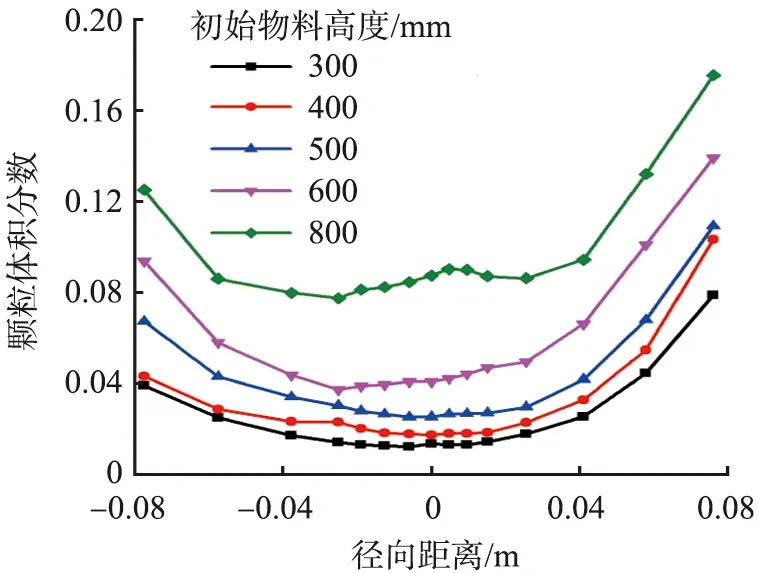
图11 不同初始物料量下流化床内颗粒体积分数的径向分布

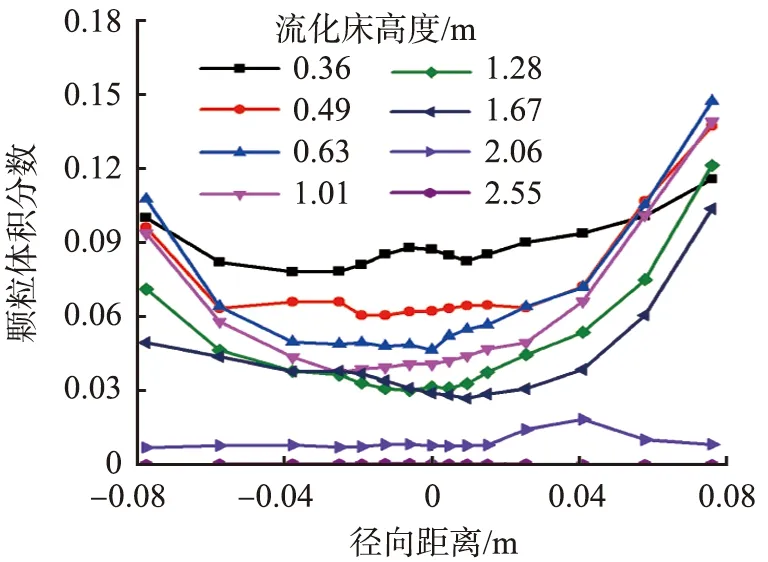
图12 初始物料量对流化床内不同高度截面径向颗粒体积分数分布的影响

3 结论

本文中对流化床内气固流动特性进行了数值模拟，研究了不同气速及不同高度初始物料量对流化床反应器内气固流动特性的影响。得出以下结论：

1)流化床内的颗粒主要累积在流化床的底部，颗粒体积分数随着流化床高度增加而减小，当气速不小于2.5 m/s时，在流化床底部的颗粒累积减少，更多的颗粒进入流化床的反应段中上部。随着气速的增加，流化床反应器中的颗粒数量分布更加均匀。

2)随着初始物料量的增加，流化床内轴向、径向颗粒体积分数均增加；流化床内的颗粒体积分数分布呈中间小、两边大的“U”形分布，而流化床内的径向颗粒速度与其相反，呈中间高、两边低的倒“U”形分布。

3)颗粒停留时间在流化床的不同高度截面分布呈现出非均匀特性。壁面附近的颗粒停留时间长于中心处，停留时间较短的颗粒与停留时间较长的颗粒相遇，使得颗粒之间的相互碰撞频繁，加剧了壁面附近的颗粒聚集。