基于低电压穿越的风电场集电线路短路电流研究

杨伟伟，王硕禾，陈 金2，牛江川，张冰华

(1. 石家庄铁道大学 电气与电子工程学院，河北 石家庄 050043；2. 河北鲲能电力工程咨询有限公司，河北 石家庄 050022)

近年来，由于双馈感应发电机(DFIG)具有调速范围广、有功与无功可独立解耦控制等优点，因此被风电场作为主要商用机型广泛使用。随着双馈式风电场的大规模并网发电，接入系统的容量也越来越大，国家电网公司对风电接入的要求越来越高。当电网发生故障时，为了避免类似甘肃酒泉等风电基地大规模脱网事故发生[1-2]，国家电网公司提高了风电场并网要求。国家标准GB/T 19963—2011《风电场接入电力系统技术规定》[3]中规定，风电场必须要具有低电压穿越(LVRT)能力，因此现有双馈风力发电机组普遍具备了LVRT能力。因为单台风机容量小，所以风电场并网结构大多为放射性拓扑型式，其中，集电系统是实现汇流功能重要环节。集电系统是指风机箱式变压器与升压变压器间的电气连接部分，包括集电线路、断路器和汇流母线等元件[4]。集电线路具有线路较长和回路较多的特点，作为重要的功率传输路径，其短路电流应该是风电场电气安全规划中考虑的重点[5-7]，因此对LVRT期间的风电场集电线路短路电流进行深入研究非常有意义。

目前，已经有一些国内和国际学者研究了风机短路电流特性。文献[7]中仿真分析了风电场提供的短路电流与故障时风电场接入系统的容量、投运的风电机组数、风速的关系，认为只根据单个因素考虑风电场保护整定是不精确的。文献[8]中计及撬棒保护，仿真分析了多种影响风电场短路电流的因素，其中故障点位置、故障类型对DFIG风电场短路电流具有显著影响，输入风速、集电阻抗主要影响短路电流暂态峰值，而撬棒阻值主要影响短路电流衰减时间常数。文献[9-10]中从DFIG数学模型出发，得到了风电场整个LVRT期间的短路电流。文献[11]中从风电场保护整定的角度出发，推导了撬棒电阻投入和LVRT全阶段的短路电流方法。文献[12]在讨论集电线路电流保护整定时认为，如果不计及非故障集电线路，则风机流入的短路电流将产生不小于5%的误差。文献[13]中通过分析LVRT控制策略对短路电流的影响机理，发现在故障期间LVRT会对DFIG的短路电流特性造成很大影响，并建立了DFIG短路电流计算的等效模型。综上，文献对风机的短路电流研究较多，但专门针对自身距离较长并且回路较多的特点研究集电线路的短路电流的文献较少。

以上述研究为基础，以双馈式风电场集电线路为主要研究对象，对作为汇流并传输功率长线路的集电线路的短路电流特性进行深入分析。首先结合风电机组LVRT期间的短路电流特性，推导出集电线路不同距离故障点短路电流的计算公式； 进一步分析影响集电线路短路电流的主要因素， 得到考虑主要因素的馈线故障短路电流的变化曲线；结合风电场中压集电点(PCC)母线电压跌落程度，得出不同故障距离集电线路短路电流的变化规律，并且分析故障线路与非故障线路对短路点短路电流的贡献；最后通过电磁暂态仿真软件PSCAD/EMTDC以某风电场为实例搭建仿真模型进行验证。

1 风电场并网结构及低电压穿越要求

1.1 风电场并网结构

图1为风电场典型拓扑机构。并网风电场一般由风机、箱式变压器、集电线路、中高压汇流母线、主变压器以及送出线路组成。风电机组以一定数量按所连接集电线路进行聚类分组。

图1 风电场典型拓扑结构

1.2 低电压穿越具体要求

近年来国家电网公司对风电场LVRT的要求标准提高。国家标准《风电场接入电力系统技术规定》[3]要求：1)当电网发生故障，在并网点电压跌落至额定电压的20%时，风电机组必须保证不脱网，且使其连续运行625 ms；2)在并网点电压跌落后，风电场并网点电压能够恢复到额定电压的90%，整个过程要在2 s内完成，之后保证风电场不脱网连续运行。

2 LVRT期间DFIG短路全电流特性分析

DFIG结构模型如图2所示。DFIG转子电路通过背靠背双脉宽调制(PWM)变流器接入电网，风机定子绕组电路直接接入电网[14-15]，转子侧变换器控制策略为定子磁链定向矢量控制，通过转子侧变换器实现发电运行状态最大风能追踪。为了达到控制电机转速的目的，采用前馈控制和磁链定向结合的方法，实现无功功率和有功功率的解耦，使得DFIG具有灵活的无功调节能力[16]。网侧变换器的控制策略以保持直流侧电压恒定和功率因数控制为目的，采用电网电压定向的矢量控制，直流侧无功功率和电压由外环比例积分(PI)调节器控制；q轴和d轴的电流由内环PI调节器控制。撬棒保护用于转子短路保护，当发生故障时，信号越限，撬棒保护投入，短接转子绕组使撬棒电阻消纳短路电流以旁路转子侧变流器，从而限制转子绕组过流和直流母线过压，以维持DFIG的不脱网运行。

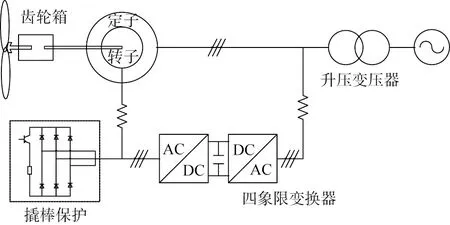
AC—交流电；DC—直流电。图2 双馈感应发电机拓扑结构

DFIG采用撬棒保护电路和四象限变换器矢量控制配合实现LVRT。当机端发生故障时，DFIG短路电流由定子输出的短路电流和功率变流器输出的短路电流组成。忽略变流器短路电流(其值很小)，可以认为DFIG机端短路电流等于定子短路电流。

采用空间矢量坐标系，定转子采用发电机惯例，理想情况下DFIG数学模型[17]为

(1)

(2)

ψs=Lsis+Lmir，

(3)

ψr=Lrir+Lmis，

(4)

Ls=Lsσ+Lm，

(5)

Lr=Lrσ+Lm，

(6)

式中：us、ur分别为定子、转子绕组的电压；is、ir分别为定子、转子绕组的电流；Rs、Rr分别为定子、转子绕组的电阻；ψr、ψs分别为定子、转子绕组的磁链；ωs、ωs-r分别为同步角速度和转差角速度；Ls、Lr分别为定子、转子绕组的电感；j为虚数单位；Lm、Lsσ、Lrσ分别为激磁电感、定子漏感和转子漏感。

根据公式(3)—(6)推导出定、转子电流的数学模型为

(7)

(8)

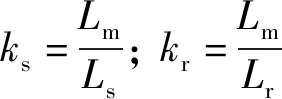
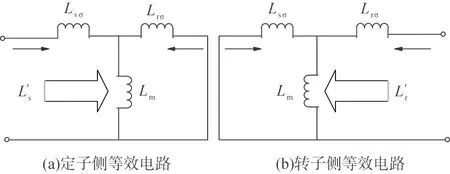
Lm、Lsσ、Lrσ分别为激磁电感、定子漏感和转子漏感。为定子绕组暂态电感；为转子绕组暂态电感。图3 故障下定子、转子暂态等效电路

当短路故障发生时，由并网型风电机组工作原理可知，此时撬棒保护电路投入，分担转子侧短路电流，因为定子、转子具有耦合关系，所以随着转子侧短路电流的减小，定子侧感应磁链必然减小，进而影响定子侧电流的值。

LVRT期间短路电流可以分为以下2种情况考虑：第1种情况为撬棒投入，变流器闭锁；第2种情况为撬棒退出，变流器工作。由式(1)—(6)可以得到DFIG暂态等值电路。图4所示为含撬棒电阻后的DFIG暂态等值电路。

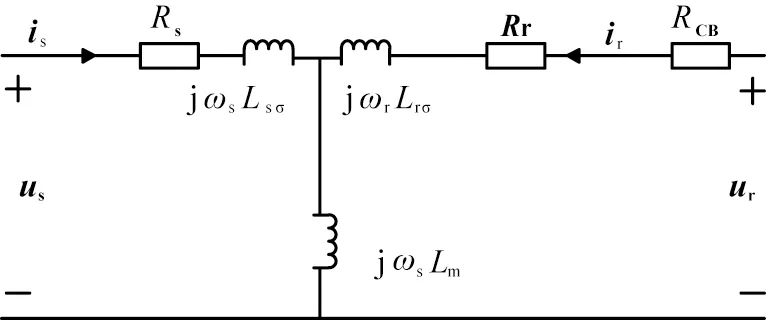
us、ur分别为定子、转子绕组的电压；is、ir分别为定子、转子绕组的电流；Rs、Rr分别为定子、转子绕组的电阻； ψr、ψs分别为定子、转子绕组的磁链；ωs、ωs-r 分别为同步角速度和转差角速度；Ls、Lr分别为定子、转子绕组的电感；j为虚数单位；Lm、Lsσ、Lrσ分别为激磁电感、定子漏感和转子漏感；RCB为撬棒电阻。图4 含撬棒电阻后的双馈感应发电机暂态等值电路

根据DFIG等值电路，经过数学推导可以得到转换到abc坐标系下的LVRT期间全电流估算(本文中以A相为例)为

(9)

(10)

3 集电线路短路电流影响因素分析

图5所示为集电线路故障时风电场等值电路，假设在图1中第1组集电线d处发生故障，图6为其简化等值电路。

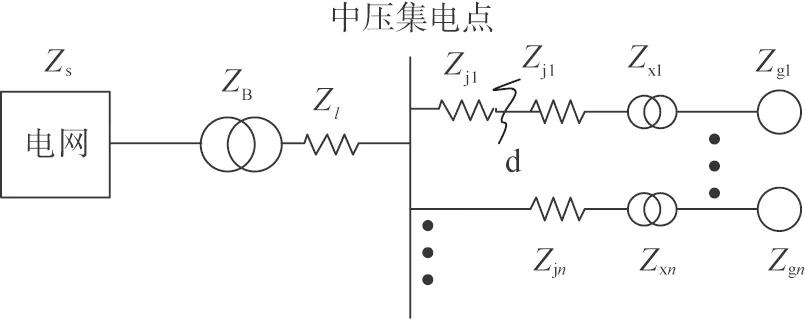
Zs、ZB、Zl分别为系统阻抗、主变压器阻抗和传输线路阻抗；Zx1、Zj1、Zg1和Zxn、Zjn、Zgn分别为第1条和第n条的箱式变压器阻抗、箱式变压器至中压集电点母线连接线阻抗和风机阻抗；为短路点d到集电线路出口处的阻抗。图5 集电线路故障时风电场等值电路

Z1∑、Z2∑、Z3∑、Z4∑分别为经过折算和串并联等值聚合之后的系统到d的转移阻抗、故障线路到d的转移阻抗、故障组相邻线路到d的转移阻抗、其他组到d的转移阻抗。图6 集电线路故障时风电场简化电路

(11)

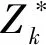
考虑风电场最大、最小运行方式可引入短路电流修正系数k，结合式(11)和简化电路可以得到d点短路电流为

(12)

特别地，当电压骤降为0时，由于风机没有零电压穿越功能，此时故障线机组将会有风机本体保护切断，因此不再提供短路电流。

分析式(10)可以发现，集电线路短路电流的数值与故障点在集电线路上的位置和风电场的运行方式以及系统的阻抗大小有关。具体关系可以由故障点与PCC点之间的距离l与流过集电线路的最大短路电流Idf的集电线路电流变化曲线(图7)来体现。图中A、B点分别为集电线路出口处第一台风电机组接入点和最后一台风电机组接入点。

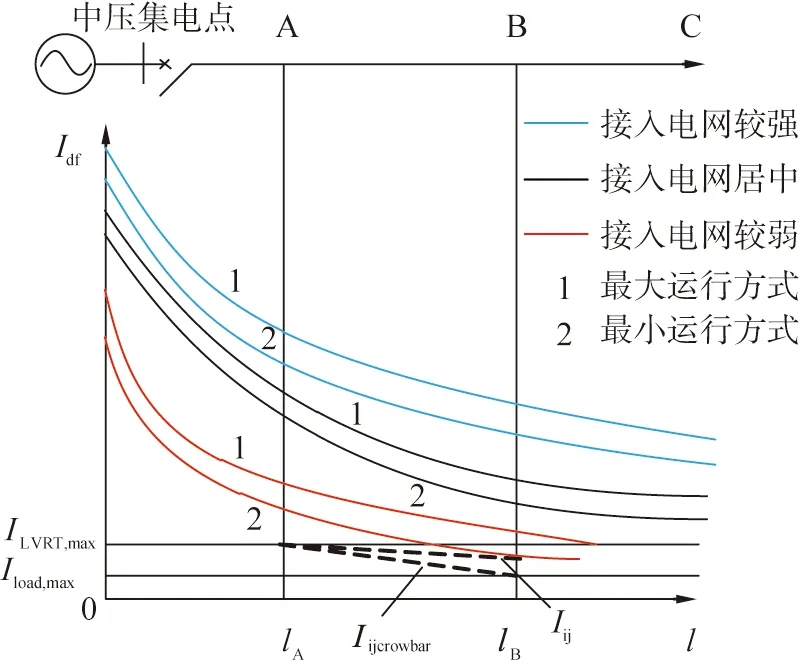
l—故障点到中压集电点之间的距离；Idf—流过集电线路的最大短路电流；ILVRT,max—故障后进入LVRT状态保持不脱网运行时集电线路的最大短路电流;Iload,max—最大负荷电流。曲线Iij、Iijcrowbar分别为未LVRT以及LVRT的风电机组故障时的最大短路电流。图7 集电线路电流变化曲线

4 仿真验证

图8所示为风电场电气仿真接线图。本文中以广西某风电场为例，采用单台1.5 MW的DFIG，其参数见表1。风机发出690 V电压，经过箱式变电器升压至33 kV，然后经过升压变压器变压到110 kV，并入大电网，风电场总容量为49.5 MW。机群分为3组，每组由11台同型双馈风机组成，由于实际搭建33台风机模型会导致仿真计算过多，为了减小计算机压力，因此第1组按11台风机并联接线，第2、3组进行了11台风机等值仿真。分3回长为7.457 km的集电线路送至汇流母线，采用的电缆RL为0.37 Ω/km，XL为0.138 Ω/km，经计算ZL为0.395 Ω/km。仿真过程中保持风速为11 m/s。系统正序阻抗为0.017 p.u.。其他设备参数设置如表2所示。设置1 s时集电线路不同位置发生短路，短路持续时间为0.3 s。

图8 风电场仿真接线图

表1 单台双馈感应电机设备运行参数

表2 变压器工作参数

图9、10分别为距离33 kV PCC母线的7 km、1 km处的集电线路三相短路短路电流和PCC母线电压仿真图。由图可知，当故障发生在距离33 kV PCC母线7 km处时，PCC母线电压跌落50%，集电线路短路电流最大值为0.25 kA，稳态值为0.1 kA；当故障发生在距离33 kV PCC母线1 km处时，PCC母线电压跌落75%，集电线路短路电流最大值为0.42 kA，稳态值为0.18 kA。

表3为距离33 kV PCC母线4 km处的集电线路三相短路短路电流和PCC母线电压数据。PCC母线电压跌落41%，稳态值为0.16 kA。对比图9、10分析发现，故障点越靠近PCC母线，电压跌落越严重，集电线路短路电流暂稳态值越大。同时，对比故障集电线电流与非故障集电线电流发现，故障集电线电流对短路点电流的贡献要比非故障集电线大很多，一般相差10倍左右。

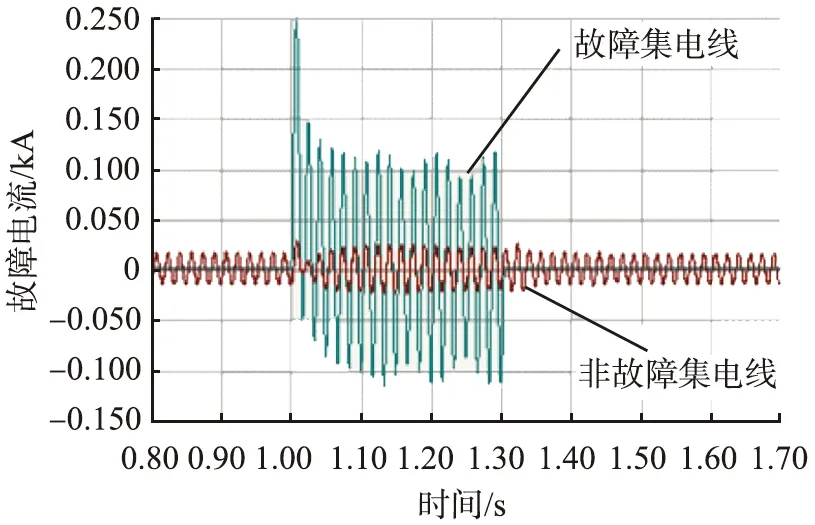
(a)电流曲线

(b)电压曲线图9 距离33 kV中压集电点母线7 km处三相短路短路电流和电压

(a)电流曲线

(b)电压曲线图10 距离33 kV中压集电点母线1 km处三相短路短路电流和电压

表3 4 km处故障时故障集电线与非故障集电线短路电流

表4为机端和熔断器处故障时PCC母线电压、短路电流、机端和熔断器位于集电线路的分支上，分析表中数据可知，集电线路分支同样符合故障点越靠近PCC母线，电压跌落越严重，集电线路短路电流暂稳态值越大的规律。上述结果验证了理论分析的正确性。

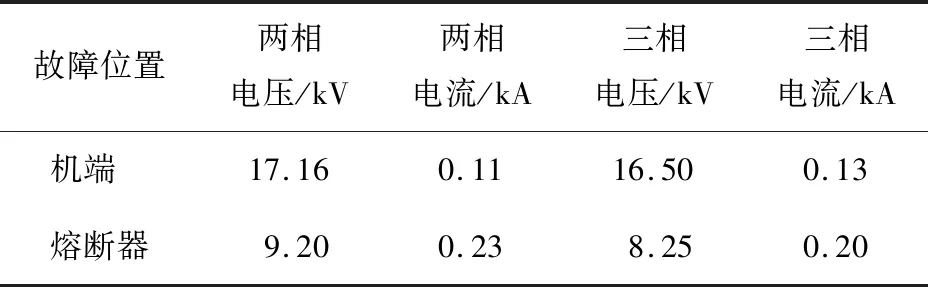
表4 机端和熔断器处故障时中压集电点母线电压、短路电流

5 结论

本文中研究了DFIG在LVRT期间的短路电流特性，通过等值简化风电场拓扑结构，推导出集电线路不同位置故障时的短路电流计算公式，结合公式分析得到考虑主要因素的集电线路短路电流变化曲线，发现短路电流变化规律。最后通过PSCAD仿真验证了故障点越靠近PCC母线，电压跌落越严重，集电线路短路电流暂稳态值越大；比较了故障线路与非故障线路对短路电流大小的贡献，即故障线路一般是非故障线路短路电流的10倍左右。该研究成果对风电场电气安全设计具有一定的参考价值。