一种双层六棱结构橡胶隔振器的隔振性能
(山东理工大学 交通与车辆工程学院,山东 淄博 255000)
振动作为生产、生活中的一种普遍现象,不仅影响工业生产设备的寿命,而且引发的噪声污染会严重威胁人类的安全与健康。为了减少生产、生活中的有害振动,研究者提出了多种振动抑制技术,如缓冲隔振、阻尼隔振、动力吸振等[1]。橡胶材料凭借成本低廉、减振性能优良、结构紧凑、形状可以任意改变、质量和体积很好控制等优点,在汽车、船舶、桥梁和建筑等工程领域中广泛应用。近年来汽车自燃现象频发,其中一个主要原因是油箱通过螺栓与车身刚性连接,在汽车运行过程中,当油箱的振动以及燃油的晃动非常剧烈时,油箱内会累积静电引燃汽油,从而造成车辆自燃。研究汽车油箱隔振问题对于改善汽车行驶安全性具有重大意义。
虽然橡胶隔振器已经广泛应用于生产生活中,但是随着生活水平的提高,人们对于所处环境及应用设施性能的要求不断提高,对于广泛应用于各种工程实践中的橡胶隔振器的要求也越来越高。目前,许多学者已经对橡胶隔振器进行了研究。王丹等[2]针对一种近似菱形结构的橡胶隔振器进行非线性有限元建模及实验对比,结果表明,隔振系统具有较小的共振频率,在低频时隔振作用很小。Lee等[3]将一种新型结构的硅胶材料模型应用于室内健身器材,显著减少了振动的传递。雷刚等[4]针对橡胶的非线性迟滞特性进行有限元建模仿真和振动实验,分析了橡胶材料的非线性动态特性,完成了橡胶隔振器动态参数的识别、数学模型的建立以及振动响应影响因素的研究。敏乾[5]利用Mooney-Rivlin模型和Yeoh模型,对列车用橡胶堆旁承进行仿真,并建立振动微分方程,通过求解微分方程,获得了橡胶堆旁承的振动传递特性。文献[6-8]中主要在橡胶隔振器材料特性及动态性能分析方法等方面进行了研究,而对于橡胶隔振器结构改进方面研究较少。
考虑到橡胶材料隔振的问题,本文中提出一种具有双层六棱结构的橡胶隔振器。为了研究该隔振器的隔振性能,首先对该新型结构橡胶隔振器进行有限元建模仿真分析,结合橡胶材料的超弹性和黏弹性特性建立合理的数学模型,然后研究该隔振器的动态性能,并把该隔振器应用于汽车油箱隔振,推导油箱基础激励隔振动力学模型,最后分析该隔振系统的动力学性能。
1 建模及有限元分析
1.1 超-黏弹性本构模型
本文中提出的双层六棱结构橡胶隔振器如图1所示。该橡胶隔振器将2个不对称的六棱体结构反向叠加起来组成双层六棱结构,旨在改善橡胶隔振器的动态性能。橡胶材料内部为大分子链状结构,并且具有超弹性和黏弹性力学特性。对该橡胶隔振器性能的研究适合采用超-黏弹性本构模型建立等效力学模型,如图2所示。橡胶材料的超弹性理论认为橡胶是各向同性不可压缩的非线性高弹性材料,具有非线性超弹性特性,超弹性性能与硬度、负载、负载频率等多种因素有关,理论研究大多采用唯象理论描述的应力与应变关系,本构关系常用应变能密度函数表示。通常基于应变能密度函数的大弹性变形本构理论描述橡胶超弹性特性,常见的超弹性本构模型有Mooney-Rivlin、Ogden、Yeoh等,其中Mooney-Rivlin模型比较常用,其应变能密度函数模型[9]为

图1 双层六棱结构橡胶隔振器

G∞—弹性模量的准静态剪切模量;Gi—黏弹性模型中的剪切模量;η—黏性系数。图2 超-黏弹性本构模型
(1)
式中:W为应变能密度;I1、I2为第一、第二偏应变不变量;Ci j为Rivlin系数,描述材料的剪切性能,下标i、j分别取0或1;N为项数;Jel为弹性体积比;Di为橡胶材料的可压缩性。
在黏弹性理论中,材料的应力响应包括弹性、黏性部分,在载荷作用下,弹性部分是即时响应的,而黏性部分需要经过一段时间才能表现出来。一般地,应力函数由积分形式给出,在小应变理论中,各向同性的黏弹性本构方程[10]为
(2)
式中:σ为Cauchy应力;t为当前时间;τ为过去时间;G(t)为剪切松弛核函数;e为应变偏量部分(剪切变形);I为单位张量;K(t)为体积松弛核函数;Δ为应变体积部分(体积变形)。
1.2 有限元模型
ANSYS有限元分析软件具有强大的动力学分析功能和良好的开放性,内部有强大的材料库,用户可以直接调用,也可以自定义各种材料。本文中橡胶材料模型的参数如下:密度ρ=1 200 kg/m3,泊松比v=0.495,超弹性模型选用两参数Mooney-Rivlin模型,取参数C10=1.047 67,C01=2.137 42[11]。黏弹性模型选取Prony级数模型,取参数α1=0.025 4,α2=0.146 6,α3=0.119 9,τ1=325.234 8,τ2=2.534 8,τ3=0.257 4[12]。
下面主要对橡胶隔振系统进行有限元建模。将系统结构处理为离散单元的集合体,即有限元模型,保持该模型的几何结构、约束条件、材料等属性与真实模型的一致,利用ANSYS有限元分析软件在计算机中进行瞬态响应分析,在达到研究目的的同时,可有效地减少时间和费用的投入。具体实施步骤如下:1)利用三维绘图软件Solidworks建立简化后的双层六棱结构橡胶隔振器模型。2)将模型导入ANSYS Workbench有限元分析软件。3)在工程材料数据库Engineering Data中设置橡胶超弹性-黏弹性本构模型材料参数。4)采用Hex Dominant单元和Body sizing网格尺寸控制进行网格划分,划分网格后的隔振器有限元模型由5 070个单元22 048个节点组成,如图3所示。5)该隔振器在工作时,上、下2个端面直接与振动源和被隔振体接触,因此,在隔振器模型的下端面施加固定约束(fixed support),另一端面施加均匀分布的垂向变化的正弦位移激励x=Xsinωt,其中X为幅值,ω为角频率。6)在瞬态分析中,根据不同的加载激励设置分析时间,通过计算,取200个正弦激励周期,时间步设置为0.01 s。7)在后处理中选择支反力(force reaction)观察隔振器在不同激励时的恢复力变化,通过对恢复力进行处理,得到隔振器的动态特性及表征性能的各种参数。

图3 橡胶隔振器有限元模型
1.3 动态特性
对隔振器进行垂向动态加载的有限元仿真分析,通过有限元仿真反映橡胶隔振器在不同激励时的垂向恢复力,并将得到的数据绘制成曲线来反映橡胶隔振器在不同激励时的动态变化。橡胶材料属于非线性弹性材料,同时具有一定的弹性和黏性,其动态响应表现出一定的非线性迟滞特性。以加载位移为横坐标,恢复力为纵坐标,对有限元仿真获得的数据拟合处理后得到位移-恢复力椭圆曲线,即橡胶隔振器非线性迟滞回线,如图4所示。迟滞回线由上、下2条组成,上方为加载曲线,下方为卸载曲线,上、下恢复力曲线关于位移反对称。橡胶材料在经受振动冲击过程中会损耗能量产生迟滞阻尼效应,即材料内部应力与应变之间存在相位差,导致恢复力和位移的非线性曲线呈现椭圆形状[13]。由此可知,迟滞回线中椭圆的面积可反映迟滞阻尼损失的大小。

图4 橡胶隔振器的位移-恢复力迟滞回线
采用不同正弦位移激励模拟该隔振器的动态工况,结合隔振器实际工作工况,分别改变正弦位移激励的幅值和加载频率进行有限元仿真。选取正弦激励频率20、50、80 Hz和正弦激励幅值0.5、1.0、1.5 mm分别施加在隔振器垂直方向进行模拟仿真。图5(a)所示为固定幅值为1.0 mm的条件下,激励频率为20、50、80 Hz时的位移-恢复力曲线,图5(b)所示为固定激励频率为50 Hz的条件下,激励幅值为0.5、1.0、1.5 mm时的位移-恢复力曲线。由图可知,当激励位移幅值保持不变时,随着激励频率的增加,位移-恢复力椭圆曲线的长半轴变长,短半轴大小不变,位置发生偏转,椭圆曲线面积变大,隔振器迟滞损失明显变大。当激励位移频率保持不变时,随着激励幅值的增加,位移-恢复力椭圆曲线仅在长半轴有所增加。由此可得,该橡胶隔振器的迟滞阻尼特性对于激励频率的变化较敏感。

(a)幅值为1.0 mm

(b)频率为50 Hz图5 橡胶隔振器的动态特性
2 数学模型及参数识别
由于橡胶材料具有较强的非线性特性,因此建立合理的数学模型对于该橡胶隔振器的研究及其更好地在各种工程实践中应用具有重要意义。图6所示为位移-恢复力迟滞回线的分解结果。以幅值为1.0 mm、频率为20 Hz的位移激励为例,可以把橡胶隔振器位移-恢复力迟滞回线分解为弹性力-位移幂函数曲线和非线性阻尼力-位移椭圆曲线[8]。这样在后续研究过程中可以把该系统看作弹簧-阻尼系统处理,进而可以应用弹簧-阻尼振动系统的理论来研究该系统。滞后非线性的数学模型有很多种,根据橡胶隔振器非线性迟滞系统特性,对于本文中提出的双层六棱结构橡胶隔振器恢复力数学模型中的非线性弹性力采用三次幂函数多项式,非线性黏性阻尼力取一次黏性阻尼,因此,本文中建立的恢复力数学模型可简化为

图6 位移-恢复力迟滞回线的分解
(3)
其中
Fk=k1x+k3x3,
式中:Fk为弹性力;k为系统刚度;Fc为非线性阻尼力;k1为线性刚度;k3为非线性刚度;c为阻尼系数。
对该模型中参数进行识别时,首先对仿真获得的数据进行整理,得到位移-恢复力迟滞回线,然后分别对非线性弹性力和非线性阻尼力中的参数进行识别。非线性弹性力数学模型为三次多项式,对仿真获得的恢复力数据利用MATLAB软件的polyfit函数进行最小二乘三次多项式拟合,所用三次幂函数多项式为
f(x)=k1x+k3x3。
(4)
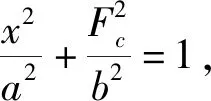
(5)
由于非线性弹性力不消耗能量,因此椭圆曲线的面积S代表阻尼力消耗的能量,则
(6)
联立式(5)、(6),可得阻尼系数c=b/aω。为了保证参数识别的准确性,对上述识别方法取n(n≥4)个周期的仿真结果数据进行重复多次识别后取平均值。
综合该隔振系统的实际工况、数学模型及参数识别方法,计算该双层结构隔振器在不同工况时的线性刚度参数识别结果,如图7所示。从图中可以看出,当激励位移幅值不变时,随着加载频率的增加,隔振器的动刚度明显变大,隔振器刚度与激励源频率呈正相关性。在定频激励时,随着加载幅值的变化,动刚度仅在24.62~25.36 N/mm波动,相对变化幅度很小,与动刚度的频率相关性相比,该隔振器动刚度的振幅相关性并不明显。由此可见,激励频率对该橡胶隔振器的刚度性能影响较大。

(a)动刚度频率相关性
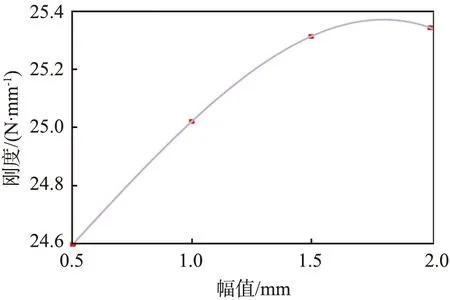
(b)动刚度幅值相关性图7 橡胶隔振器在不同工况时的线性刚度参数识别结果
3 非线性动力学分析
本文中提出的隔振器在应用于减小汽车油箱的振动时,2个端面分别与油箱外壳和车身直接接触。当汽车运动时,来自路面的激励会引起车身的振动,在隔振器的作用下,车身传递到油箱的振动被大幅削弱,进而减小了汽车油箱内燃油的晃动,降低了因燃油晃动产生静电的可能性。
为了方便计算分析,仅取一个隔振器单体结构模型进行动力学分析,简化后的动力学模型如图8所示。假设汽车运行时路面的不平使车身受到一个基础激励,隔振器简化为质量-弹簧-阻尼系统,进而该系统可以被视为单自由度有阻尼振动系统。其中,油箱简化为质量块M,xs为基础正弦激励。以基础振动为激励,应用第2节中识别的刚度系数k和阻尼系数c,得到单自由度有阻尼系统动力学方程为

k—系统刚度;c—阻尼系数;x1—质量块M的位移;xs—基础激励。图8 橡胶隔振系统简化力学模型
(7)
式中:m为油箱简化质量块M的质量;x1、xs分别为质量块M、基础激励的位移。
令z=x1-xs,对式(7)进一步整理,得
(8)
其中
xs=Xssinωt,
z=Zsin(ωt-φ),
式中:φ为激励与响应的相位差;Xs为激励的幅值;Z为响应幅值。
根据图8所示的非线性动力学模型,为了得到该振动系统的稳态传递特性,需要对式(8)进一步化简求解。图8所示的系统最终要求的是质量块M的位移x1相对于基础激励xs的传递特性,因此,令x1=Xsin(ωt-φ),其中X为质量块M的响应幅值。质量块运动可以表示为x1=z+xs,将z=Zej(ωt-φ)与xs=Xsejωt代入式(8),整理得
(9)
进一步得到
x1=z+xs=(Ze-jφ+Xs)ejωt=
(10)
由式(10)可得隔振器的相对传递特性为
(11)

隔振传递率T为系统振动后位移响应幅值与位移激励幅值的比值,T的大小代表隔振系统的隔振效果,是评价隔振系统性能的重要指标。T越小,表明通过隔振系统传递给设备的振动越小,隔振效果就越好;反之,隔振效果越差。对于乘用汽车而言,油箱大多数都安装在车身上,而车身结构的振动频率分布在20~1 000 Hz,汽车在正常行驶时,车身结构的振动频段主要集中分布在20~80 Hz[14]。由此,基于隔振系统的数学模型参数识别方法,结合动力学分析中的相对传递特性,即可得到该隔振器部分工况下的刚度、阻尼参数及隔振传递率,如表1所示。

表1 幅值为1 mm时橡胶隔振系统恢复力模型辨识参数和力传递率
为了直观表明隔振器的隔振效果,基于表1中的数据,绘制隔振器隔振传递率变化曲线(如图9中实线所示),并与文献[15]中的环形发动机橡胶隔振器的隔振效果(如图9虚线所示)进行对比。由图9可知,本文中提出的隔振器具有较小的共振频率和共振峰值,共振放大区频率范围相对较小,振动响应在达到最高峰时激振频率仅约为15 Hz,激振频率在超过共振频率后,振动响应迅速衰减。可见,该隔振器在较低频激励时隔振作用很小,但在高频时隔振效果非常显著,相应地,在车身结构振动频带范围内,对振动的衰减也非常大,最大振动衰减率约为94.5%。

图9 橡胶隔振器的隔振传递率曲线
4 结论
本文中提出一种双层六棱结构的橡胶隔振器并研究其性能,得到以下主要结论:
1)对该双层六棱结构橡胶隔振器进行振动仿真及参数识别,结果表明,外界激励的频率是影响橡胶隔振器的隔振性能的主要因素,幅值是次要因素。
2)建立了隔振系统的动力学微分方程,对其进行求解,并结合汽车车身结构振动特点进行了分析,结果表明,该隔振器具有较小的固有频率和共振放大区频率范围,激励频率在超过系统固有频率后,隔振传递率显著减小,可有效减少车身传递到油箱的振动,进一步改善了汽车行驶的安全性。

