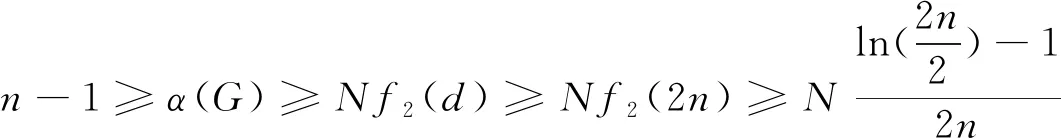一类广义Ramsey数R(B2,Kn)界的研究
涂巧霞,王 艳
(黄冈师范学院 数学与统计学院,湖北 黄冈 438000)
Ramsey理论是组合数学的一个重要分支,它广泛应用于计算机科学、信息论以及决策学等领域.在Ramsey理论研究中,关于求解Ramsey数,在逻辑分析、并行计算和计算几何等计算机科学领域起着至关重要的作用,同时,许多实际问题的求解,如贮藏问题等等,也往往导致求一个相关图的Ramsey数.

一般地,确定Ramsey数是一个非常困难,且尚未完全解决的问题.可以通过构造一些特殊的极值图,从而得到它的下界或上界.如,C5不含K3,同时有C5的补图也是C5,于是对于完全图K5的这样一种红蓝着色,将子图C5染成红色,余下边同样构成一个C5,染成蓝色,此种着色既不含红K3,也不含蓝K3,所以有R(3,3)>5;在C8中增加四条对角线形成一个独立数为3的无三角形图,在完全图K8中,将上述加了四条对角线的C8这样的子图染成红色,余下边染成蓝色,于是这种染色既不含红色三角形,也不含蓝色K4,故有R(3,4)>8.
1 相关定理
利用概率方法作有关Ramsey数和一些特殊图的Ramsey数的研究[2-7].本质上概率方法是一种粗糙的计数论证方法,但一方面可以用来断定具有某种特性的图的存在性,另一方面,一定程度上给出了Ramsey数的一些非线性的界.应用概率方法,可以得出一类广义Ramsey数的非线性界.
定理1若B2=K2+2K1,Kn是具有n个顶点的完全图,则对足够大的n,一定有
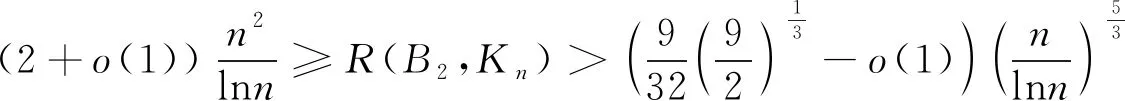
(1)
由于B2是完全图K4的子图,因此,定理1的界同样也适用于Ramsey数R(4,n).
推论1若B2=K2+2K1,Kn是具有n个顶点的完全图,则对足够大的n,一定有

(2)
2 相关引理
引理1设N=N(n),n=o(N)(n→∞),那么任意ε>0,若n足够大,则有
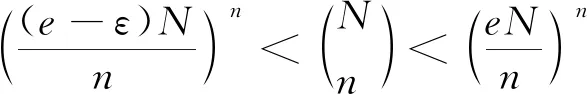
(3)
引理2令G为阶为N的图,平均次数为d,若G中任意顶点v的邻域N(v)生成子图G[N(v)]的最大次不超过a,那么
α(G)≥Nfa+1(d)
(4)

(5)
3 主要证明
本文主要对定理1中出现的式(1)利用概率方法给出证明.
定理1的证明:令B2=K2+2K1,易看出B2=K4-e,Kn是具有n个顶点的完全图,文中主要利用概率方法寻找一类特殊R(B2,Kn)数的上下界,首先考虑下界,考虑在概率空间G(N,p)中的随机图.S是阶为n的点集,构造指示函数如下:

(6)


(7)
类似构造函数YT如下:

(8)
于是
E[YT]=Pr[BT]=p6
(9)
进一步,令
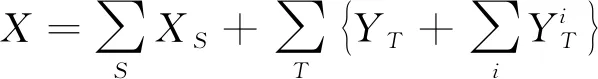
(10)
据数学期望的线性性质,有

(11)

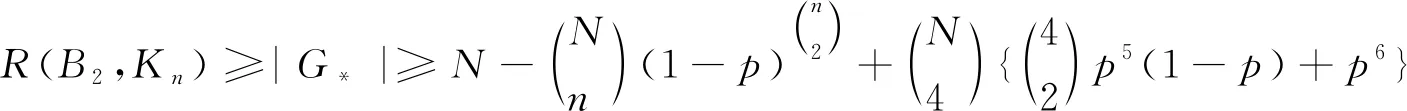
(12)
寻找合适的N使得|G*|尽可能大,可以考虑取

(13)
则有

(14)
据引理1,又有

(15)


(16)


(17)
为了证明广义Ramsey数R(B2,Kn)的上界,任取阶为N=R(B2,Kn)-1的图G,且图G不含B2,并有α(G) (18) 所以 (19) 经典Ramsey数R(k,l)的确定,已知R(1,n)=1和R(2,n)=n, 并且有R(k,l)=R(l,k),故只须考虑k和l均大于2的情形,表1给出已确定的经典Ramsey数. 表1 已确定的经典Ramsey数R(k,l) 其它尚未给出精确值的经典Ramsey数R(4,n)目前已有相关界的讨论,大多数界均为组合数形式或者递推式,均为构造特殊图的方法得出.推论1给出的Ramsey数R(4,n)界的确定一定程度上给出了经典Ramsey数R(4,n)精确值的取值范围.