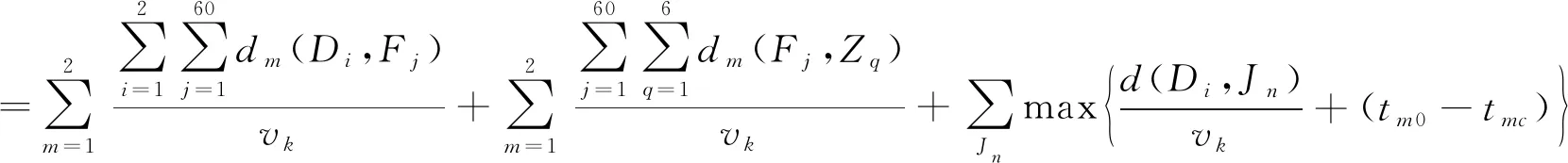多波次导弹发射车的安全转移路径
方 舒,库在强
(黄冈师范学院 数学与统计学院,湖北 黄冈 438000)
导弹作战是未来战场的主要作战方式之一,导弹在发挥威力给予敌军重创的同时,保护自身的安全性与隐蔽性也成了军事研究的热点问题,多波次导弹齐射作为一种重要的作战方式,保障导弹安全快速到达发射点位成为了提高我方生存概率的重要手段。 杨宝珍[1]针对战争时某一重要道路被破坏对作战计划的影响,充分运用GIS路径分析功能,进行最佳机动路线的选定;王桐等[2]在一定的假设下,构建了基于马尔卡夫链的多波次导弹作战模型,用于战前迅速的部署;宋志华等[3]研究了单车单波次和单车多波次行动规划问题的求解,在此基础上,以多车多波次为研究对象,建立了多阶段网络流模型,将最优行动方案问题转化为在网络流模型中寻找最小费用最大流问题;郝亮亮等[4]以Dijkstra算法为基础,建立了不同波次导弹打击任务求解方案,不仅能使整体暴露时间最短,还可以保证导弹发射后轨迹不相交。在前人已经研究的内容基础上,考虑到路网情况复杂,不同车载装置速度不同,单行双道错综复杂,道路节点冲突等问题。
现本文以第十四届全国研究生数学建模竞赛E题为背景,考虑在复杂路况情况下Dijkstra算法的适应性以及求解程序上进行必要的简化。假设有某部队参与作战行动,基本信息如下:为了提高导弹部队的生存能力和机动能力,常规导弹大都使用车载发射装置,在接受多波次发射任务后,每台发射装置只能载弹一枚,从待机地域携带导弹沿道路机动到指定发射点位实施发射,完成任务后立即机动到转载地域装弹,再机动至下一波次指定的发射点位实施发射,连续两波次发射时,每个发射点位使用不超过一次,具体道路分布概况如图1。
(1)车载发射装置情况为:车载发射装置有A、B、C三类,数量依次为 6、6和12台,在主干道路上的平均行驶速度依次为70、60和50公里/小时,在其他道路上的平均行驶速度依次为45、35和30公里/小时;
(2)待机区与作战区情况:2个待机地域D1、D2。所属作战区域内有转载地域Z1~Z6,发射点位F1~F60,各转载地域最多容纳2台发射装置,每一发射点位只能容纳1台发射装置,单台转载作业需10分钟;
(3)道路情况:道路节点为J1~J62,主干道路是双车道,可以双车通行;其他道路均是单车道,只能在各道路节点处会车。
部队接受发射任务后,需要为每台车载发射装置规划每个波次的发射点位及机动路线,要求整体暴露时间最短。本文将解决以下问题:若该部队接受两个波次的齐射任务,每个波次各发射24枚导弹,如何规划具体发射点位分配及机动路线方案,使整体暴露时间最短。并且考虑到攻防双方的对抗博弈,道路节点受到攻击破坏会延长整体暴露时间,量化分析该路网最可能受到敌方攻击破坏的三个道路节点。
1 两波次导弹发射最短整体暴露时间
1.1 问题解决流程设计
本文主要研究问题为车载装置完成两个波次齐射任务的暴露时间最短问题,合理进行24辆车载装置路线规划是问题解决的关键,因此将整个导弹转移区域转化成图,并采用邻接矩阵的形式进行表示,导弹转移过程如图2所示。
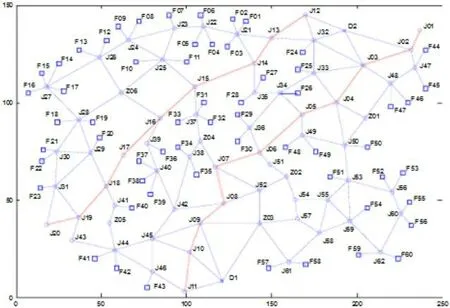
图1 作战区域道路示意图

图2 车载装置完成两个波次齐射任务流程图
1.2 主要符号说明
多波次导弹作战过程背景信息庞大,涉及车载发射装置、待机区与作战区、道路节点及单双车道等多重分类情况,现列出其中主要符号说明如表1所示。
1.3 道路节点地位均衡下的暴露时间
第一波次发射前车辆已经配备好导弹从待机区域向发射点位出发,第二波次齐射前车辆状态分为两个连续的阶段,从发射点位至转载地域进行装弹与从转载地域出发至发射点进行第二波次导弹的发射,两个波次导弹发射前后车辆穿行于2个待机区域,60个发射点位,62个道路节点,6个转载区域,单双车道共同组成的复杂路网中,由于车载装置型号不同所带来的速度差异,需要合理进行路线规划安排,避免道路节点冲突,减少等待时间,缩短整体暴露时间,在第一波齐射前的运载过程中,车辆均处于暴露状态,为了减少暴露时间,安排速度快的车辆去相对较远的路线,安排速度慢的车辆就近去发射点位。根据Dijkstra算法得出从待机地域D1、D2出发到各个发射点之间的距离以及合理的车辆安排行驶路线,然后安排不同类型的车辆去完成任务使得整体的暴露时间最少,暴露时间模型为如下:

表1 主要符号说明一览表
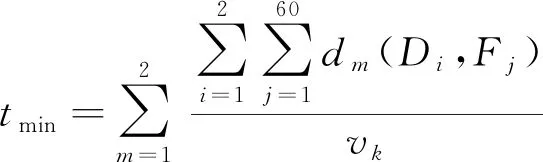
(1)
采用Dijkstra算法来解决本文的最短路径问题。根据所给条件,相邻点之间有连线的记为两点之间的距离,若两点之间没有连线则记为 ∞,同一点之间的距离则为0,通过利用Matlab编程[5-6]求出任意两点之间距离以及找到从某一点到终点的具体路径,再根据车载装置的不同速度,计算出每条路径上车辆行驶时具体的暴露时间。由于各个装载导弹的车辆要求齐射,因此,若最慢的车花费的时间是tm0,其余车辆所花费的时间为tmc,则为了减少本次发射的总体暴露时间,其他车辆适当晚点出发以避免到达发射点位的等待时间,从而减少暴露时间,特将时间差值记为tm0-tmc,由于第一辆车出发时间记为0时刻,则任意一辆车到道路某节点Jn的时间为:
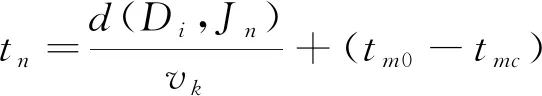
(2)
为使导弹在两个波次的发射任务的整体暴露时间最短,依据图1发射任务流程图,将整个过程分为三个阶段,第一阶段为从待机区域到第一波次导弹发射点位,第二阶段为从第一波次导弹发射点位到转载地域,第三阶段是从转载地域到第二波次导弹发射点位。将此三阶段的暴露时间之和视为两个波次发射任务的整体暴露时间。求最短暴露时间的前提是知道距离,因此通过Matlab软件导入数据,利用内部函数dist命令计算出路网图中各个线段之间的距离。
1.3.1第一阶段分析
从待机区域出发的车已经携带导弹,不必再去转载地域装弹,因此只需考虑寻找距离待机区域最近的发射点位即是本阶段问题的最优解。考虑到不同发射装置类型的速度不同,将安排距离较远的路径由速度较快的车完成任务,则较短的路径安排较慢的车去执行,并且本文所给信息中要求24枚导弹齐射,为了减少整体暴露时间,特此将距离较近的装载车晚些发射,从而减少装载车辆在发射点位的等待时间。第一阶段24辆携带导弹的车辆分别从D1、D2出发,利用Dijkstra算法计算出各个车辆的行驶路线,其中部分具体路线为:
……
通过Dijkstra算法可以得到最短暴露时间的发射点位与相应的转载地。给每个道路节点一个特定的标号,通过Dijkstra算法反向计算出路径[7],并根据路径安排去指定的发射点位发射导弹。依据相应的路线和道路及每辆车的速度,计算每辆车到发射点的时间,如果全部可以到达既定发射点,则完成第一波发射任务,如果有部分未能及时到位,则说明路径过程中某个道路节点出现了冲突,从而计算出等待时间来增加暴露时间,最后得出总体的暴露时间。因此确定最短路线的同时要考虑道路的冲突问题:道路分为主干道和非主干道,主干道为双行道,而非主干道为单行道,俩者车辆的容量有所差异。
(1)对于单行道来说,每次只能通过单方向的车,记fn1,c(X,T)为编号为c的车辆到达单行道道路节点n1,假设若有整数r,满足r≠c时有:
fn1,c(X,T)=fn1,r(X,T)
[fn1,c(X,T),fn1,c(X,T)+tn1,c]∩[fn1,r(X,T),fn1,r(X,T)+tn1,r]≠Ø
此时称该道路节点有冲突。
为了更好的量化道路冲突,合理采用0-1规划函数,对道路冲突进行描述,令:
对该目标进行优化:
maxP{hn1(X,T)}=1
(3)
(2)对于双车道来说,只要保证车辆之间超过2分钟的时间间隔就可以错开道路冲突,因此,在考虑双车道路节点n2的时候,通过计算车辆通过时间来安排车辆通行时间,从而避开道路冲突。若多个车辆进入同一个道路,则对于车辆集C(c1,c2,c3…c24) :
①对于任意一个运输方案(X,T),计算每个车辆到达该道路节点的时间。
②把每辆车到该道路节点的时间按照从此小到大的顺序排列:
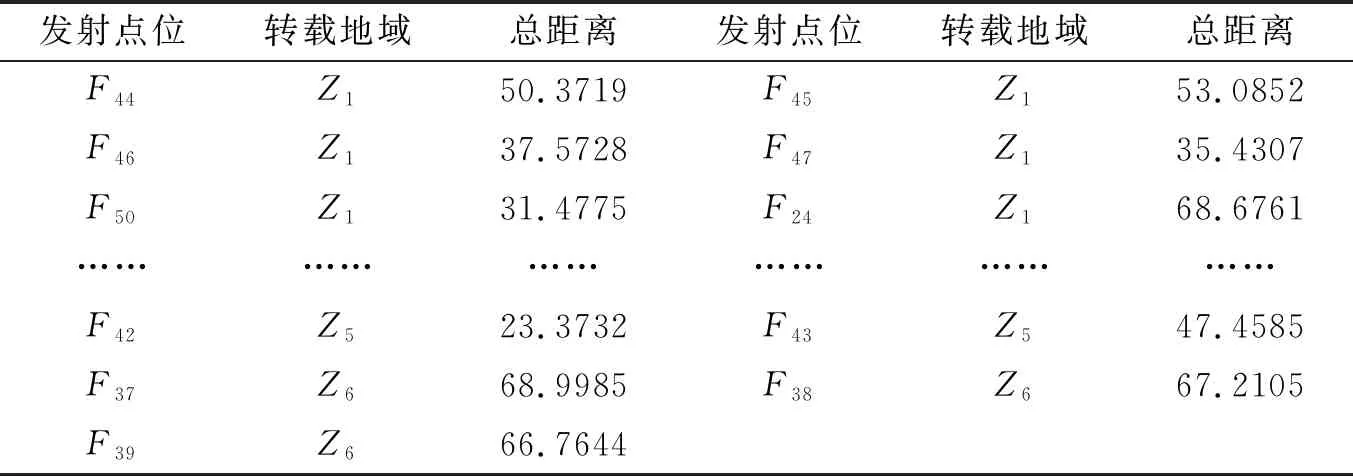
Fn2,c1(X,T) gn2,c1(X,T)=fn2,c1(X,T) 计算gn2,c1(X,T),其中Mn2表示相应节点通过的车辆次数,具体实现步骤如下: 步骤一:令r=1,dn2=0 步骤二:令ar=1,s=r+1 步骤四:返回步骤三,直到s=24 步骤六:令G←G,G={c};r=r+1 步骤七:重复步骤二到步骤五 ,直到r=24 优化目标: maxP{dn2(X,T)=0,n2=c} (4) 根据上述分析,在第一阶段 24 辆车到达各个发射点位的总暴露时间为52.0 h。 1.3.2第二阶段分析 第二阶段各个发射点的车辆去转载地域装导弹,采用多重目标规划的方法,将24辆车分配到距离它们较近的转载地域,这样可实现使第二阶段车辆的总体暴露时间最短,根据该思路,具体计算步骤如下: (1)计算各转载地域到该 24 个发射点位的距离,其中d(Fj,Zq)(j=1,2…24,q=1,2…6),部分如表2所示: 表2 部分转载地域到发射点位的总距离 (2) 把上述距离按照Fj从小到大的顺序排列: d(F1,Z1) d(F2,Z1) …… d(F24,Z1) (3)找到每个发射点到相应的转载地域的最短路径距离: d(F1,Z1),d(F2,Z1)…d(F24,Z1) (4)分析道路的容量情况,考虑单行道和双行道的具体时间,道路的处理方式同第一阶段,从而避免道路冲突。 maxP{hn1(X,T)}=1 (5) 对于多行道来说,只要保证车辆之间超过2分钟的时间间隔就可以错开道路冲突,因此,在考虑多行道的时候,通过计算车辆通过时间来安排车辆通行时间,避开道路冲突。 (5)计算每辆车到各个道路节点的时间,判断等待车辆的等待时间。各个发射点位的车辆部分路径如下: 通过上述路径图的时间分析,可以清晰的计算出第二阶段车辆从各个发射点到转载地域的总时间为35.9 h。 1.3.3第三阶段分析 根据条件限制,第二波次齐射计算中需去掉第一阶段已发射导弹的发射点位,第三阶段的思考可以使用第一阶段中采取的计算模型来选取最短路径使的暴露时间最短,此时的出发点是各个转载地域,对于第三阶段的具体分析如下: (1)将第一阶段的发射点位全部去掉,剩下的所有发射点位,利用Dijkstra算法得出从各自的转载地域到剩余发射点的最短距离及最优路径。 (2)分析道路的容量情况,避免道路冲突,具体处理如第一阶段。 (3)计算每辆车到各个道路节点的时间,判断车辆的等待时间。 部分具体路径分别为: 通过计算得出第三阶段发射装置的整体暴露时间为44.9 h。综合前三个阶段分析,最终得出完成两个波次的齐射任务过程中整体的暴露时间为t=52.0+35.9+44.9=132.8 h。 本文前半部分主要是对多波次导弹完成两个波次发射任务的最短暴露时间进行建模分析,但考虑到双方的攻防博弈,从总的道路节点中筛选出最易受敌方攻击的道路节点具有重大意义。就系统科学分析法来说[8-9],道路节点的重要性等同于破坏性,由于道路节点受到损坏时,需要维修道路节点,或者绕到最近的道路节点,此时会延迟甚至阻碍发射装置按时到达指定发射点位,将增加整体暴露时间,即等待时间,现对本文涉及到的62个道路节点进行审查,从敌方视角来考虑,选择破坏三个重要道路节点,使得整体暴露时间最长即可达到目标效果: 由前文可以知道,在没有任何道路节点被破坏的情况下,分别找到相应的从两个待机区域出发所行驶的路径: (6) 及相应的暴露时间,此时的暴露时间记为: (7) 此时,每辆车的行驶路径已经确定,从中找到行驶最短路线及所有节点通过车辆的次数,用MATLAB软件中的内部sort命令进行排序,可以得到:62个道路节点通过的车辆次数M={M1,M2,M3…M62}及该车辆在两波齐射中所需的总时间。并且由于道路分为主干道和非主干道,主干道的行驶速度较快,因此,道路节点选择出现冲突优先选择主干道。在前文最短暴露时间分析的基础上,两个波次齐射任务的24 辆发射装置的具体行驶路线很清楚的呈现了出来,也可以知道各个道路节点被使用的情况,哪些道路节点对于整体暴露时间的影响较大,敌方优先选择这些道路节点作为他们目标的概率相对来说就会更大。 选择每个道路节点去掉所节省时间后的最大值,并按照节省时间来排序,从而确定易受到敌方攻击的三个道路节点。根据前文的路径图,可以得出被使用频率最高的4个道路节点,如表3所示: 表3 道路节点被使用次数 由于J15,J50被使用次数相同,考虑到J15这个道路节点处于主干道的位置,敌方相对于J50会优先选择破坏J15,因此最有可能受敌方破坏的道路节点是J37,J32,J15。在确定最可能受敌方攻击的道路节点后,就可以提前对其完整性进行保护,以及对一旦破坏后采取哪种应急路线方案可以最小化延长整体暴露时间进行规划。 导弹作战效能是衡量一国军事发展的重要指标,本文所研究的多波次导弹发射模型背景信息量大,需要考虑多重约束条件,如主干道与非主干道的速度差别,单行道与双行道的车辆容纳信息,以及道路节点的冲突,暴露时间最短问题,具有较强的实用性,将多目标的多波次导弹打击问题转换为求取相应路网中等效的最短路径问题,运用Dijkstra算法依次求解三个阶段最佳路径,进行最短暴露时间的求解,针对道路节点冲突问题,合理采用0-1规划模型进行解决,为了减少发射区等待时间,依车载装置速度差异分批次出发。与此同时考虑去掉哪三个道路节点后使得总体暴露时间最长,从另一个角度给模型优化提供新思路,这对于导弹在未来战场最大化发挥作用具有一定的参考意义,另外,本文对于具体问题的求解方法,对于相似的路径规划问题同样具有可解性。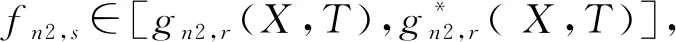
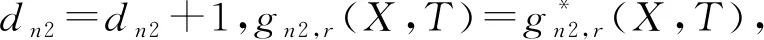
2 道路节点冲突下的暴露时间