基于山地城市主干道交通流特性分析

班越+吴启顺+朱嘉

摘要：本文通過对重庆某城市主干道一条车道全天道路交通流数据采集，运用MATLAB软件建立了流量、速度以及时间占有率之间的相互关系模型，重点对流量与时间占有率之间的关系进行分时段比较分析，得出了混合交通流下的城市主干道在平峰时段速度相对较高和集中的趋势，时间占有率在20%时，为交通状态发生变化的临界点。

关键词：交通流；时间占有率；主干道；特性；临界点

中图分类号：U491.1 文献标识码：A

引言：道路通行条件、驾驶心理与行为、交通流组成差异使得交通流特性表现不同[1]。山地城市道路宽幅有限，道路坡度大，车流构成多样化等因素，导致其交通流特征不同于平原城市。本文通过分析典型山地城市重庆城市主干道交通流量、速度、时间占有率之间相互关系，挖掘其城市主干道交通流特性，为后续城市道路规划、管理控制提供参考。

1数据来源

本文数据是通过视频检测设备（检测精度达90%以上）在渝鲁大道车道某日6：53～10：48实时采集所得。渝鲁大道是双向6车道，从路中央到两边分别标号1、2、3，分别检测3条道路的车流量、速度、时间占有率等数值。

2 交通流特性分析

2.1 速度-流量关系

从图1速度-流量散点关系中，可以看出渝鲁大道主线分流内车道存在明显的非拥挤与拥挤状态。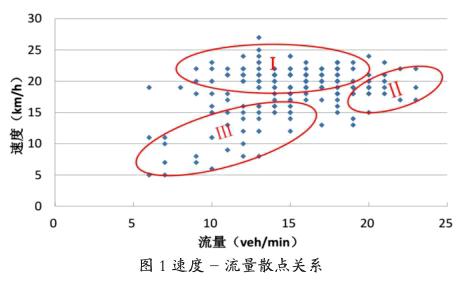

如图1考虑，重庆市城市主干道大体有三个阶段划分，城市干道受到速度限制，混合车流条件下的城市干道跟传统的快速路速度-流量关系略有不同。阶段Ⅰ、Ⅱ描述的是白天速度与流量之间的变化关系。具体来说，阶段Ⅰ表现的是白天平峰时期车辆自由行驶的道路交通状况，此阶段车辆的速度随流量增加表现出稳定状态，最大速度可达至60km/h，直到流量增加到某一值，速度随着流量增加开始减小。阶段Ⅱ是早晚高峰道路开始出现拥挤的阶段，交通流呈现间断性，短时内随机会出现车辆激增现象，然后是排队消散过程的反映，车辆由拥挤状态向排队消散的过程[1]。阶段Ⅲ中区域数据点对应流量少、速度低主要原因是夜间行驶的车辆，以特型和大型车辆为主，通行的时间段集中在22：30至次日早晨7：00。

2.2 流量-时间占有率关系

本文选取了某道路2015年12月3日全天每1min流量和对应的时间占有率，从图可以看出，流量与时间占有率成反λ模型[1]，时间占有率0～18%之间，流量与时间占有率之间接近线性增长关系，超过18%时流量随着时间占有率的增加有下降趋势，因此临界时间占有率约为18%。如下图所示。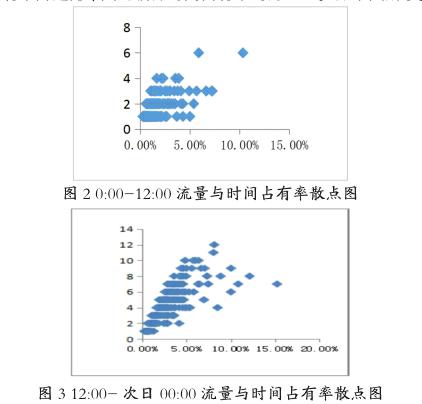

从图2可以获悉凌晨至7：00车流量少，经统计该时段内车辆平均行驶速度为47km/h，道路畅通；早晚高峰时段出现拥挤时的时间占有率分别在25%、18%左右（图3）。平峰上午时段（图2）和夜间时段（图3）车辆流量与时间占有率之间呈现明显的线性关系，一定范围内，随着时间占有率增大，流量增加，此时道路交通需求远小于道路通行能力，车流能够实现畅通行驶[3]。比较图2与图3，可以发现，夜间驾驶员车速选择范围较白天平峰时段要大，平峰白天时段车辆速度一致性高，道路通行秩序较夜间要好。

总结：从速度、流量、时间占有率之间的散点图可看出，重庆市主干道交通三参数间关系跟传统的交通流模型有着相似的地方，也表现出差异。这种差异主要来自在混合车流中低速慢行的重型车辆存在、交叉口信号控制、驾驶特性、道路条件共同作用。在一定范围，时间占有率越大，速度越离散，白天时间段内速度与时间占有率之间明显表现线性关系，速度集中50km/h～60km/h。主干道的速度与流量之间的关系跟城市快速路速度-流量模型曲线明显不同，在低流量下，速度并没有呈现负线性关系，这跟城市干道是否采取限速措施相关[3]。城市干道交通流在拥挤即将出现（时间占有率>20%）的时候表现出短时流量“跳跃”现象，交通状态发生变化的临界点，交通流状态比传统的高速公路、公路或快速路更加脆弱。

参考文献

[1] 王炜. 交通工程学 [M]. 南京：东南大学，2011

[2] 王建军，严宝杰. 交通调查与分析[M]. 北京：人民交通出版社，2004

[3] Jiang R，Wu Q.S.Wave properties of anisotropic dynamics model for traffic flow. Transportation Research Part B Methodological . 2012