非共面组合节理剪切破坏特征研究

崔志猛，范祥, 2，谢永利, 2

非共面组合节理剪切破坏特征研究

崔志猛1，范祥1, 2，谢永利1, 2

(1. 长安大学 公路学院，陕西 西安 710064；2. 长安大学 陕西省公路桥梁与隧道重点实验室，陕西 西安 710064)

为探究非共面组合节理在剪切荷载作用下的破坏规律，利用室内试验和数值计算的方法建立不同夹角的组合节理试样和数值模型，并进行相同荷载和剪切速率的测试。以试验和数值相结合的方法，对不同夹角的节理剪切结果、剪切应力曲线和微裂隙进行对比分析。同时对微裂隙产生过程、不同试样的组合节理夹角与其峰值和残余剪应力的关系分别进行分析。研究结果表明：相邻组合节理的贯通方式与组合节理的夹角有关，当夹角小于或等于90°时，相邻组合节理的贯通遵循就近原则；当夹角大于90°时，贯通裂纹右侧终端由组合节理交叉点向下移动并最终到达下部尖端；随着夹角的增大，产生微裂隙的破坏方式由剪切破坏为主逐渐转为由拉剪破坏为主，并且，对于夹角较大的组合节理贯通之后，会产生以张拉破坏为主的次生裂纹；剪应力曲线的峰值与残余值呈负相关，峰值剪应力与组合节理夹角呈正相关而残余应力与之呈负相关。

组合节理；直剪；组合节理夹角；微裂隙

由于节理、裂纹、断层等广泛存在于岩体中，使岩体成为一种非连续介质，从而在岩体内部形成软弱结构面。基于节理的几何形状以及在岩体中不同的分布类型对岩体的力学性质有十分重要的影响，不少学者采取了各种各样的方法对节理岩体进行不同荷载条件下的试验研究[1−3]，这些方法归结起来主要包含理论分析、数值模拟和室内试验3个方面。节理可分为连续节理和断续节理。其中，断续节理包含共面节理和非共面节理，深入研究非共面节理岩体的力学性质有助于解决建设工程中存在的实际问题，如隧道围岩稳定、巷道冒顶、边坡失稳等。对非共面节理岩体剪切失效方面问题的研究引起了越来越多领域内学者的兴趣[4−5]。在节理岩体力学性质的研究中，由于现场取样难度较大，且现场试验中不可控因素较多，所以人工类岩材料被用于制作节理岩体，并用室内试验的方法研究节理岩体的力学行为。在人工节理岩体的制作中，对于节理的制作有多种不同的方法。起初，一些研究通过在浇筑的模型中插入薄铁片或云母片的方法制作节理[6−9]；后来，随着液压切割技术的成熟，有学者通过液压切割的方法制作节理[10]；现在，随着3D打印技术的发展，一些研究人员利用CT扫描和3D打印技术制作成空间不规则节理，此方法能够更加真实的仿制自然岩体节理，因此有着良好的应用前景[11−12]。大量的工程实践表明，在剪切荷载下，非共面节理岩体的破坏过程主要包括裂纹的起裂、聚集和贯通3个阶段，而且贯通后所形成的完整贯通面，会使节理岩体的抗剪强度降低，导致岩体结构破坏失稳[13]。经过大量研究，发现断续岩体节理的破坏形式可根据其结构面受力形式分为张拉破坏、剪切破坏、拉剪破坏[14−15]。综上所述，虽然众多学者对非共面节理岩体的破坏机理进行了深入细致的分析，但有关非共面岩体节理的形状和在岩体内部的分布形式对岩体剪切失效的影响还有待进一步研究。本文选取石膏为原材料，制作不同组合节理夹角的非共面人工节理试样，并对其进行室内剪切试验，同时利用离散元软件PFC2D建立与室内试样相同的数值模型并进行加载。根据室内试验的剪切结果，并结合离散元数值模拟对剪切过程中试样的破坏和裂纹扩展进行分析。

1 非共面组合节理岩体模型试验

1.1 节理布置

本次试验采用室内试验和数值模拟相结合的方式，试样尺寸及节理布置如图1(a)所示，所有试样尺寸均为150 mm×150 mm×30 mm(长×宽×厚)，节理的交叉点位于剪切面上，而且节理关于剪切面对称，每条组合节理边的平面尺寸为20 mm×2 mm(组合节理每条边的长×宽)。为组合节理2个边的夹角，其大小的取值分别为30°，60°，90°，120°和150°。试样的剪切方法为：首先，把剪切面下部固定，然后，在试样剪切面上部采取由左向右的剪切方向(图4所示)。如图1(b)所示，3条节理等距(40 mm)布置，两端节理距试样边界35 mm。

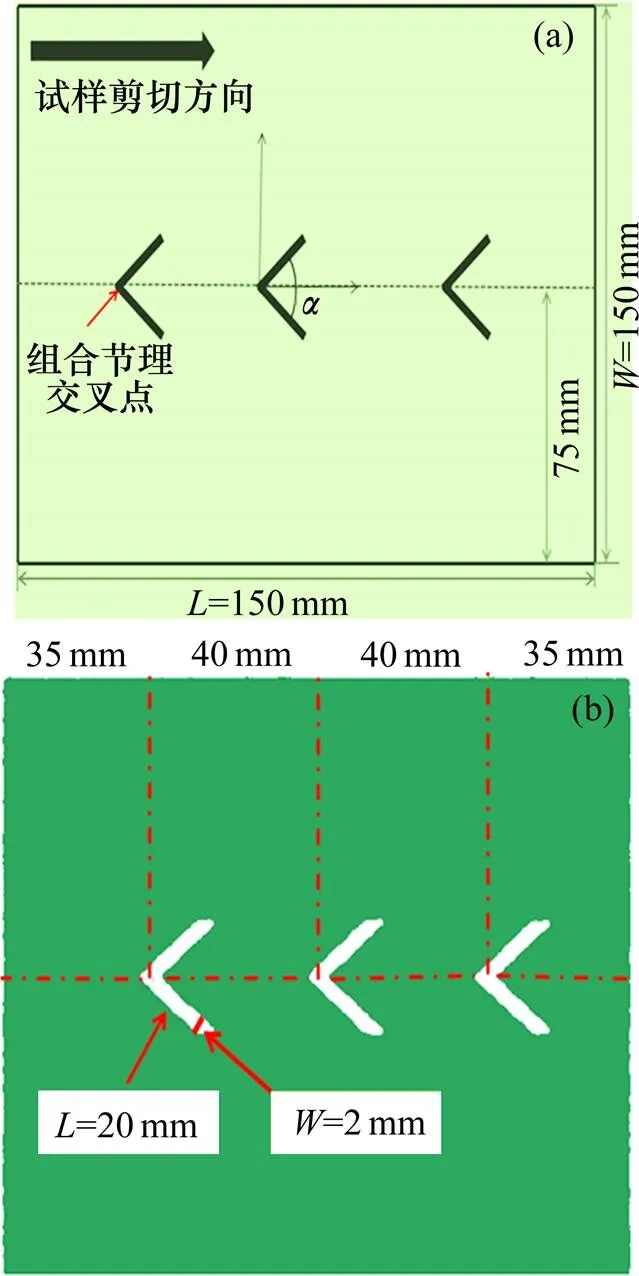
(a) 剪切示意图；(b) 节理间距及尺寸

1.2 试样制作

为了便于表示，本文以字母S表示室内试验试样，以NS表示数值模型试样，其后数字表示组合节理夹角，例如：S90表示组合节理夹角为90°的室内试验试样；NS90表示组合节理夹角为90°的数值模拟试样。

在人工试样的制作中，石膏是一种制作节理岩体良好的材料，被广泛用于制作人工岩石试样。本次试验所用试样的制作方法：首先，与文献[13]选取的石膏与水的比例相同，以1:0.35的重量比混合并搅拌均匀，在钢模内部的表面涂抹一层凡士林。然后，将制作好的流塑态石膏倒入钢模之中并振捣密实，防止石膏中有气泡滞留从而导致试样内部产生孔洞。最后，待试样处于可塑态时，将2 mm厚的云母片板提前切割成尺寸为20 mm×30 mm大小，并将2个切割好的云母片按照组合节理的夹角竖直插入试样。由于石膏从可塑态到凝固态所需时间大约为20 min，所以节理制作时需要快速进行。试样制作完成后，放置20±2 ℃的室温中养护，拆模后的部分试样如图2所示。

(a) S120；(b) S150

1.3 试验加载

如图3所示，本次试验所用的加载装置为RYL-600微机控制岩石剪切流变仪，此仪器是数字化、高精度的德国进口设备，由除水平加载装置、竖向加载装置和伺服控制系统外，还包括输入输出设备[16]。本试验的加载过程如下：首先，将试样放置并固定，其次，将水平加载装置沿导轨移动至法向加载孔与法向应力装置相吻合处并施加大小为0.5 MPa的法向荷载，最后，施加2 mm/min的水平速率开始剪切。整个剪切过程由全数字化伺服控制系统控制，以保证剪切过程精确伺服，并在剪切过程中同时记录剪应力、剪位移、法向位移等参数。

图3 试验加载装置

1.4 数值模型

在岩体力学中，数值模拟作为一种试验方法被广泛应用于岩体节理的力学研究[1, 13]，笔者采用离散元软件PFC2D建立数值试样，由于本次室内试验所用试样与文献[13]中所用试样为同一批，所以数值模型的标定参数也可根据文献[13]进行标定。标定的具体做法为：

1) 对不含节理的试样进行压缩和巴西劈裂 试验；

2) 得到试样的抗拉、抗压强度及泊松比等宏观参数；

3) 用试错法对数值试样进行标定；

4) 对标定后的数值试样进行压缩试验，得到的应力−应变曲线与室内压缩试验所得的应力−应变曲线进行对比；

5) 如果试验对比相差较大，则返回继续修正细观参数，直到应力−应变曲线一致为止。

详细的细观参数标定值[13]如表1所示，建立如图4所示的数值模型试样，试样大小、节理的尺寸和夹角与室内试样一致。在PFC2D中，采取随机分布颗粒生成法共生成40 358个颗粒。加载速率与室内试验所给一致，荷载步约为1.28×106，剪切位移为3 mm。

表1 数值试样细观参数

图4 数值试验加载示意图

2 试验结果分析

2.1 节理破坏的模式

根据文献可知[15]，节理岩体无论在压缩还是剪切荷载下，其破坏过程中总是伴随着微裂隙的产生和聚集。在非共面节理的加载过程中，微裂隙总是先出现于节理尖端附近，并在不同的节理尖端之间聚集形成贯通裂纹。本文对于非共面组合节理进行分析发现，不同组合节理夹角的试样，其裂纹的贯通形式存在显著的差异。如图5(a)所示，S30的贯通裂纹存在于相邻节理之间，并从左侧节理的上部尖端近似沿直线扩展到右侧节理的下部尖端，然而对于S60和S90裂纹，其贯通形式如图5(b)所示，相邻节理的裂纹只存在于上部节理的尖端和组合节理的交叉点之间。但是对于S120，其贯通裂纹的右端，由节理交叉点向下移动(图5(c))。当组合节理夹角到达150°时(S150)，贯通裂纹的右端点近似到达下部尖端位置。总而言之，非共面组合节理的裂纹贯通形式与组合节理夹角有关，当=30°，60°或90°时，裂纹在相邻2条节理尖端的扩展存在于剪切面的上部并遵循就近原则，当=120°或150°时，裂纹的扩展存在于相邻组合节理的上下尖端之间并遵循就近原则。可能是因为当=120°或150°时，组合节理交叉点的尖端效应减弱，而相邻组合节理的上下尖端附近产生的裂隙向剪切面发展并由于其贯通遵循就近原则，所以裂纹贯通路径近似呈一条直线段。本文中所提的“就近原则”是指：裂纹在2个端点之间贯通，其贯通路径近似为一条直线段。此外，上述裂纹的破坏形式均在本次试验中得到验证，并将在下文中详细叙述。

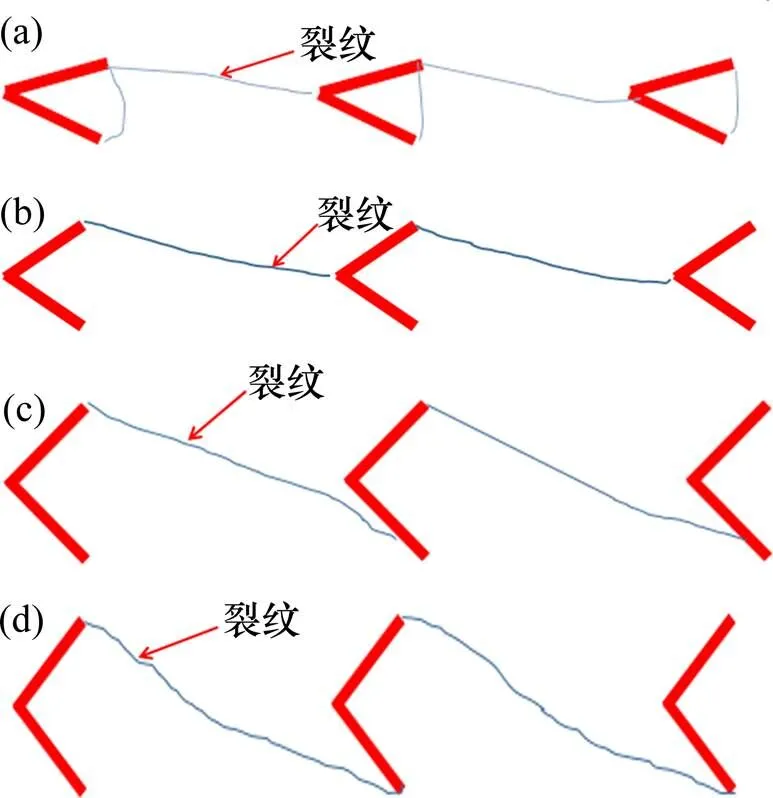
(a) 组合节理S30；(b) 组合节理S90；(c) 组合节理S120；(d) 组合节理S150

2.2 非共面组合节理的剪切破坏过程

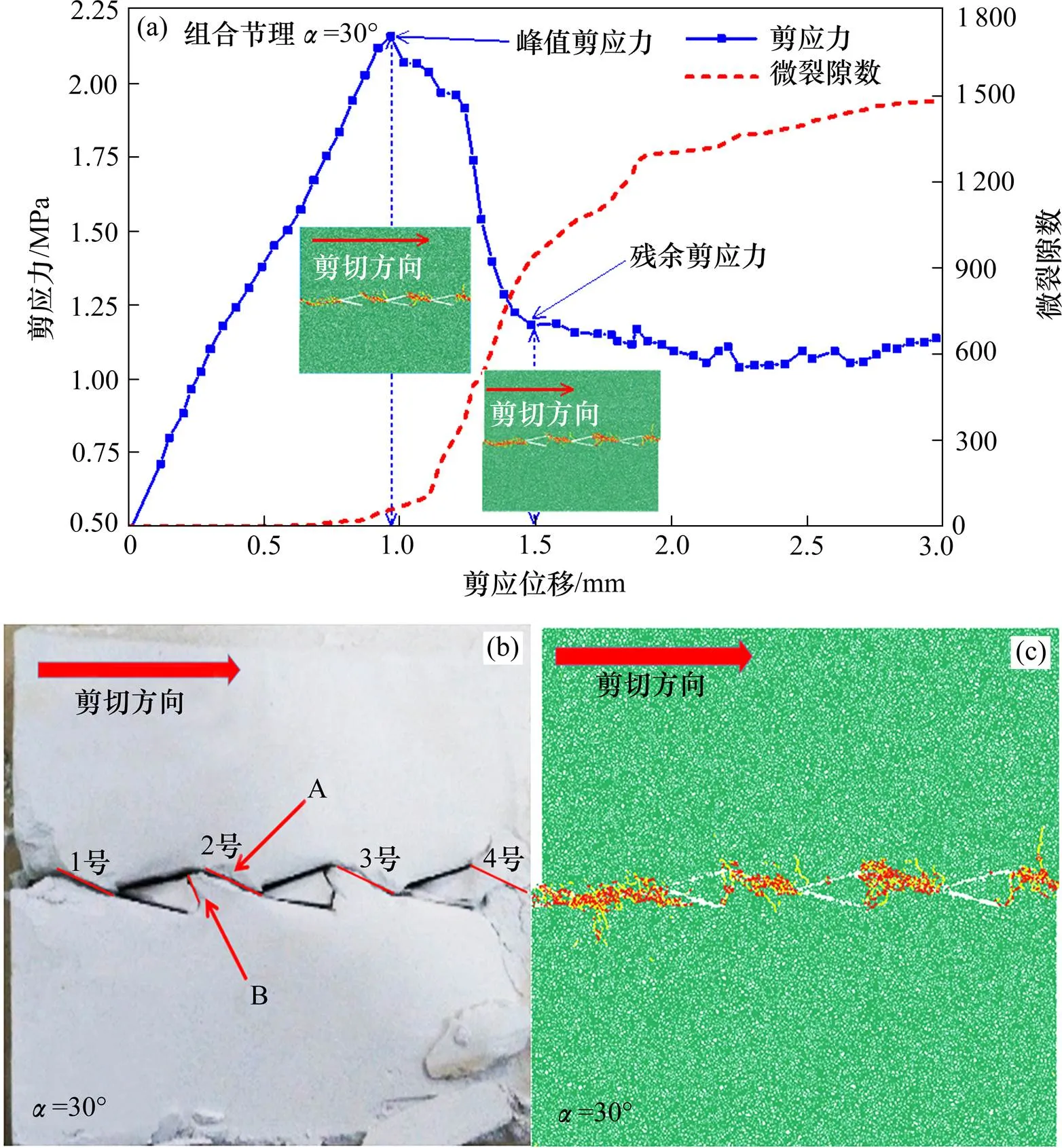
为了探究非共面组合节理的破坏规律，本文选取组合节理夹角为30°，90°和120°的节理试样，并结合图6(a)，7(a)和8(a)所示的剪应力、微裂隙−位移曲线进行对比分析。在数值试样结果图中，绿色表示组成试样的颗粒，黄色表示拉伸破坏产生的微裂隙，红色表示剪切破坏产生的微裂隙。

对比S30，S90和S120的剪应力、微裂隙−位移曲线发现(图6(a)，7(a)，8(a))，剪应力峰值随着组合节理夹角的增加而增加，而峰值对应的位移值则是随的增加而先增加后减小，但峰值对应的位移值均处于1.0～1.5 mm之间；微裂隙数在峰值剪切应力之前几乎没有增长，这可能是因为在剪切峰值之前，剪切曲线呈线性增长，此阶段颗粒之间的黏结处于弹性或弹塑性变形状态，故没有发生破坏。但在剪应力峰值和残余值之间的阶段，所有试样的微裂隙数都快速增长，此阶段部分颗粒之间的黏结在受拉伸或剪切力的作用下，其变形到达极限状态并发生拉伸或剪切破坏，故此阶段的微裂隙快速增长。在剪应力处于残余阶段时，微裂隙开始由快速增长变为缓慢增长，并逐渐停止变化，从剪切应力曲线的残余应力值对应的数值模型图(6(a)，7(a)，8(a))中可以看出，微裂隙已完成聚集并开始贯通，故微裂隙在此阶段逐渐停止增长。

(a) S30剪应力、微裂隙−位移曲线；(b) S30；(c) NS30

S30和NS30的剪切结果如图6(b)和6(c)所示，其节理之间裂纹的连接形式与图5(a)相符合，对于S30，由于组合节理夹角过小，所以除相邻节理之间形成的贯通裂纹A外，其同一组合节理的上下2个边的尖端也产生贯通裂纹B，对比S30和NS30可知，室内试样的剪切结果和数值模拟的试验结果一致。此外，从NS30中可知，贯通裂纹A的产生主要以剪切破坏为主，但裂纹B的产生主要以拉伸破坏为主。在本次试验中，组合节理试样中的裂纹B仅在=30°时发生。对比图S30和图S90可知，1号贯通裂纹的右侧端点从左端节理的交叉点向下移动到节理下部的尖端，而且此种现象也可以从数值试样的剪切结果中得到验证(图6(c)和图7(c))。从两者的数值试样可知，NS30中的1号裂纹以剪切破坏为主，而NS90中对应的1号裂纹以拉剪破坏为主。对比S90和S120发现，2号和3号贯通裂纹的右端从节理交叉点向下移动，这种现象与图5(c)描述的一致，结合NS90和NS120可知，120°组合节理的贯通裂纹的张拉微裂隙开始增多。不仅如此，就其破坏形式而言，随着增加，贯通裂纹的破坏形式从以剪切破坏为主逐渐演变成以拉剪破坏为主。出现这种现象可能的原因是相邻节理的上下尖端近于剪切面附近时，裂纹的形成路径也近似位于剪切面附近，而剪切面上主要以剪应力为主，所以较易形成以剪切破坏形式为主的贯通裂纹；此外，由于节理夹角较小，造成同一节理的2个尖端之间的部位抗拉能力较弱，在剪切的作用下产生挠动，容易导致拉伸破坏；随着的增大，组合节理的尖端距剪切面的距离增加，而在剪切荷载下，剪切面的剪应力最大并易发生剪切破坏，但是裂纹的起裂具有尖端效应并通过尖端扩展[13]，所以试样中的1号裂纹在剪切面的左端点和左端节理的下部尖端形成贯通。此外，由于尖端距离剪切面的增加，微裂隙的产生不再以剪切破坏为主，而是发生拉剪破坏。

(a) S90剪应力、微裂隙−位移曲线；(b) S90；(c) NS90

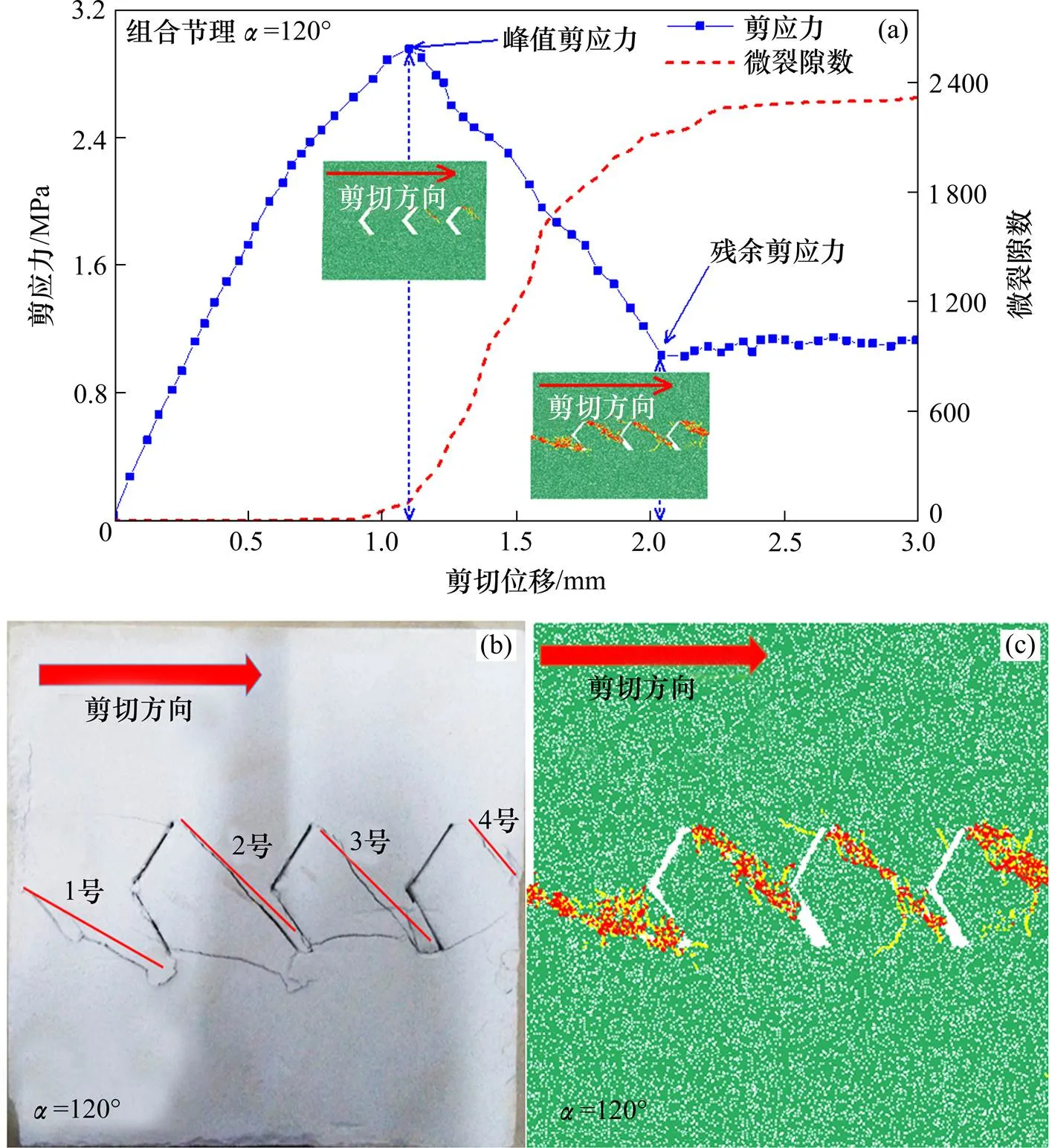
(a) S120剪应力、微裂隙−位移曲线；(b) S120；(c) NS120

3 微裂隙扩展及峰值残余应力

3.1 微裂隙扩展过程

在剪切试验中，岩体裂纹的起裂、聚集和贯通的规律对岩体的剪切力学性质有着重要的影响。数值试样是由颗粒与接触黏结构成，而本文的数值试样颗粒之间接触模型为平行黏结接触模型，此接触黏结的破坏形式分为剪切破坏和拉伸破坏，当试样受剪切荷载时，颗粒之间的接触黏结被剪断或拉坏，从而形成微裂隙，本文以NS150模型为例，结合微裂隙增长曲线和玫瑰微裂隙图说明不同位移时刻微裂隙的变化规律。图9(a2)～9(e2)中，裂隙玫瑰图的环向表示微裂隙的倾角，径向表示微裂隙的条数。本次试验中微裂隙的倾角为平行于剪切面的平面与微裂隙之间的夹角。

在岩体的剪切试验和压缩试验中，研究人员主要把裂纹的产生过程分为起裂、聚集和贯通3个阶段。微裂隙的产生主要发生在岩体的弹塑性和塑性变形阶段，如图9(a1)所示为裂缝起裂开始的数值试样，从图9(a2)可知，此时的剪切位移为0.5 mm，微裂隙数仅为2条，并且通过玫瑰裂隙图可知，其倾角在55°～75°之间。从图9(a1)到9(b1)时段，裂纹处于起裂和扩展并存的过渡阶段，在此过程中微裂隙从不同的节理尖端附近起裂，并沿相邻节理上下尖端扩展，微裂隙数开始逐渐增多，且其倾角的范围开始向大小2个方向扩展，但多数微裂隙的倾角为50°～70°之间；在图9(b1)到9(c1)时段，微裂隙开始大量增多且对比图9(b2)和9(c2)可以发现，除倾角为50°～70°之外的微裂隙相对增多；当剪切位移达到1.75 mm时，即图9(d1)所示的数值试样，裂纹已经扩展完成并且已开始贯通，此时，其数量增长开始缓慢降低；到剪切结束时刻(图9(e1)和9(e2))，节理之间的裂纹已经完全贯通，且出现近乎垂直于贯通裂纹的方向并向相邻节理下尖端的部位扩展的拉伸裂隙。

(a1), (a2) 0.5 mm；(b1), (b2) 1.25 mm；(c1), (c2) 1.5 mm；(d1),(d2) 1.75 mm；(e1),(e2) 3 mm

3.2 峰值及残余应力分析

由3.1部分所述，根据组合节理不同的夹角，非共面组合节理的裂纹扩展形式可以分为2种，当组合节理夹角=30°，60°或90°时，裂隙的扩展由尖端到相邻节理交叉点；当组合节理夹角=120°或150°时，裂纹由上部尖端扩展到相邻节理的下部尖端。这种节理夹角与裂纹扩展形式的关系对节理模型的剪应力峰值和残余值的影响分析如下：如图10(a)所示，非共面组合节理的峰值剪应力与夹角之间的关系，无论是室内试样还是数值试样的峰值剪应力都随夹角近似呈线性变化，随着倾角的增大而增大，在夹角达到150°时，峰值剪应力达到最大值。而且，室内试验峰值剪应力拟合线和数值模拟峰值剪应力拟合线的差异不大(图10(a))。出现这种现象的可能原因是组合节理的尖端随着倾角的增大距离剪切面越远，贯通裂纹的长度亦随之增大，所以在剪切过程中形成的微裂隙增多，导致剪应力峰值也随之增大。但是峰值剪应力随组合节理夹角的增长幅度并不大，其范围在2 MPa以内，这可能是因为法向应力只有0.5 MPa, 导致剪应力峰值较小，其不同倾角的增长幅度也较小。

图10(b)为残余剪应力与组合节理夹角的关系曲线，与峰值剪应力曲线不同，残余剪应力与组合节理夹角呈负相关。随着组合节理夹角的增加，残余剪应力逐渐减小，且由拟合线公式可知，无论是室内试验还是数值模拟，其节理夹角与残余剪应力呈一次线性关系。通过观察3.1部分不同组合节理夹角节理的剪应力曲线图发现，在同一模型中，峰值剪应力越大则残余剪应力越小，这表明在节理剪切模型中，剪应力峰值与残余剪应力二者呈负相关性。因为在非共面组合节理的剪切试验中，裂纹的起裂、发展与贯通均在相邻节理的尖端产生，并近似呈一条直线段。而且节理尖端距剪切面的距离越远，裂纹的起裂所需的应力越大，裂纹贯通后破坏性越大，抗剪强度也就越小，故峰值剪应力与残余剪应力二者呈负相关性。但与图10(a)相同的是残余剪应力随组合节理夹角变化范围也不大，原因可能与上述相同，其法向应力仅为0.5 MPa。

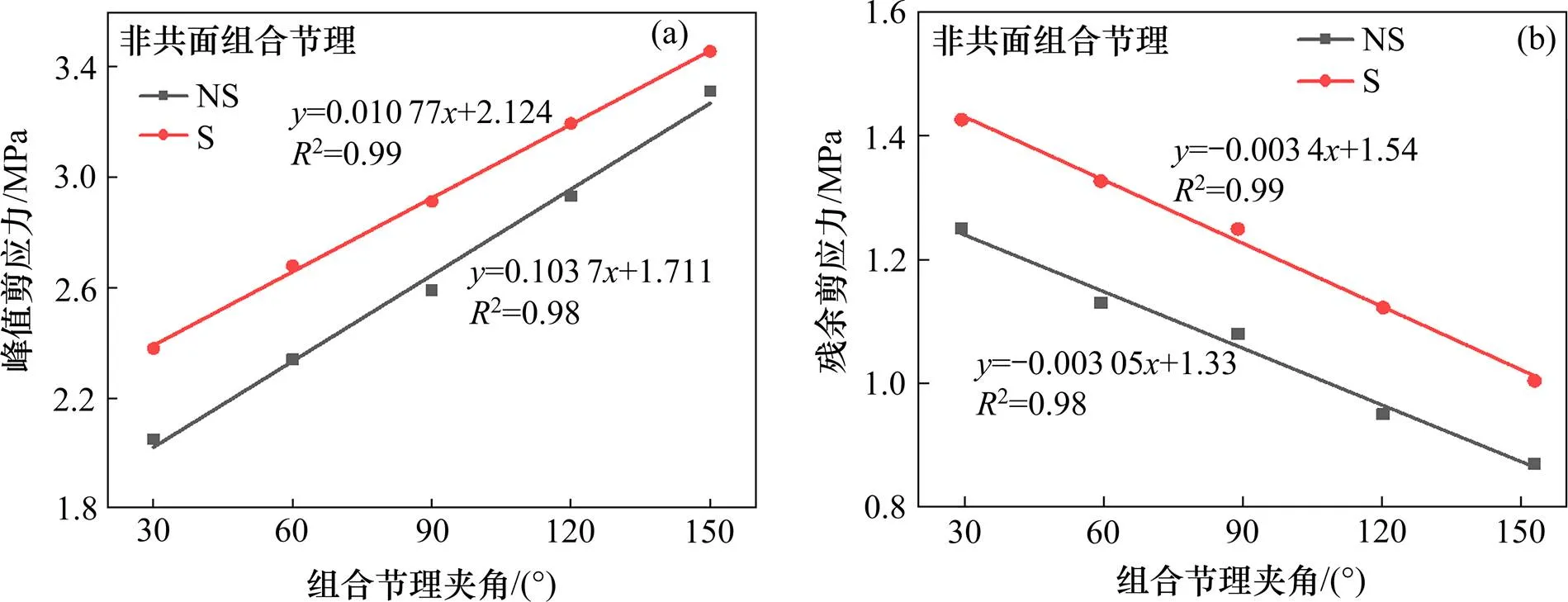
(a) 峰值剪应力与组合节理夹角关系；(b) 残余剪应力与组合节理夹角关系

4 结论

1) 在室内试验和数值模型的剪切过程中，剪切面为承受剪应力最大且极易发生破坏的薄弱面，节理尖端距离此剪切面越近，对应的剪应力−位移曲线的峰值越小；节理尖端距离此剪切面越远，对应的峰值剪应力越大。

2) 非共面组合节理的夹角对微裂隙演化有重要影响，当节理夹角=30°，60°或90°时，裂纹在节理上尖端和相邻节理交叉点处起裂、扩展和贯通，但当节理夹角=120°或150°时，裂纹起裂的位置逐渐由组合节理的交叉点向下移动到组合节理的下部尖端。

3) 不同裂纹的微裂隙产生、聚集和贯通不同时发生；随着组合节理夹角的增加，微裂隙的破坏方式由以剪切破坏为主变为拉剪破坏为主，而且裂纹贯通之后还会出现以张拉为主的次生裂纹。组合节理的峰值剪应力和残余剪应力随组合节理夹角的变化而呈一次线性变化，但不同的是，峰值剪应力随组合节理夹角呈正相关，而残余剪应力随组合节理夹角呈负相关。峰值剪应力和残余剪应力二者呈负相关。但可能是法向应力较小的原因，二者随节理夹角的变化幅度不大。

[1] 范祥, 曹日红. 规则表面节理剪切力学行为研究[J]. 武汉理工大学学报, 2017, 39(2): 54−60. FAN Xiang, CAO Rihong.Study of shear behavior of regular surface joint[J].Journal of Wuhan University of Technology, 2017, 39(2): 54−60.

[2] 邓华锋, 潘登, 许晓亮, 等. 三轴压缩作用下断续节理砂岩力学特性研究[J]. 岩土工程学报, 2019, 41(11): 2133−2141. DENG Huafeng, PAN Deng, XU Xiaoliang, et al. Research on mechanical characteristics of intermittent jointed sandstone under triaxial compression[J].Geotechnical Engineering, 2019, 41(11): 2133−2141.

[3] 王桂林, 张亮, 许明, 等. 单轴压缩下非贯通节理岩体损伤破坏能量演化机制研究[J]. 岩土工程学报, 2019, 41(4): 639−647. WANG Guilin, ZHANG Liang, XU Ming, et al. Energy damage evolution mechanism of non-across jointed rock mass under uniaxial compression[J]. Geotechnical Engineering, 2019, 41(4): 639−647.

[4] 张黎明, 陈国庆, 李志波, 等. 共面断续岩桥直剪试验破坏过程研究[J]. 长江科学院院报, 2018, 35(10): 120− 125, 142. ZHANG Liming, CHEN Guoqing, LI Zhibo, et al. Failure process of coplanar discontinuous rock bridge in direct shear test[J]. Journal of Yangtze River Scientific Research Institute, 2018, 35(10): 120−125, 142.

[5] 董航宇.不规则岩石节理剪切力学特性试验研究[D]. 焦作:河南理工大学, 2017. DONG Hangyu. Experimental study on mechanical shear properties of irregular rock fractures[D]. Jiaozuo: Henan Polytechnic University, 2017.

[6] 朱鹏瑞, 万飞, 王航, 等. 预制非贯通单组裂隙岩石模型力学参数试验研究[J]. 有色金属(矿山部分), 2018, 70(4): 73−77, 92. ZHU Pengrui, WAN Fei, WANG Hang, et al.Mechanical parameters of prefabricated non-connected single group of jointed rock mode[J]. China Nonferrous Metals (Mining Section), 2018, 70(4): 73−77, 92.

[7] 王奇智, 夏开文, 吴帮标, 等. 预制平行双节理类岩石材料板动态破坏试验研究[J]. 天津大学学报(自然科学与工程技术版), 2019, 52(10): 1099−1108. WANG Qizhi, XIA Kaiwen, WU Bangbiao, et al.Dynamic failure of simulated rock mass plate containing two parallel cracks[J].Journal of Tianjin University (Natural Science and Engineering Technology), 2019, 52(10): 1099−1108.

[8] 曹吉胜, 戴前伟, 马德鹏. 预制节理岩体卸荷损伤破坏机理及声发射特征试验研究[J]. 中南大学学报(自然科学版), 2018, 49(6): 1465−1471. CAO Jisheng, DAI Qianwei, MA Depeng. Experiment research on damage mechanism and acoustic emission characteristics of rock mass with prefabricated joints under unloading condition[J].Journal of Central South University (Natural Science), 2018, 49(6): 1465−1471.

[9] 段国勇, 孙旭曙, 张景昱. 非连通预制节理试件力学特性试验研究[J]. 河南理工大学学报(自然科学版), 2019(5): 152−158.DUAN Guoyong, SUN Xushu, ZHANG Jingyu. Experimental research on mechanical properties of prefabricated disconnected joint samples[J].Journal of Henan Polytechnic University (Natural Science), 2019(5): 152−158.

[10] YANG S Q, JIANG Y Z, XU W Y, et al. Experimental investigation on strength and failure behavior of pre-cracked marble under conventional triaxial compression[J]. International Journal of Solids and Structures, 2008, 45(17): 4796−4819.

[11] 王本鑫, 金爱兵, 赵怡晴, 等. 基于CT扫描的含非贯通节理3D打印试件破裂规律试验研究[J]. 岩土力学, 2019(10): 1−9. WANG Benxin, JIN Aibing, ZHAO Yiqing, et al. Experimental study on fracture law of 3D printed specimen with non-consecutive joints based on CT scanning[J]. Rock and Soil Mechanics, 2019(10): 1−9.

[12] 徐竟航, 张志奇, 彭亮. 3D打印技术在节理岩体试样制备中的应用与研究[J]. 铁道勘察, 2019, 45(3): 70−74. XU Jinghang, ZHANG Zhiqi, PENG Liang.Application and research of 3D printing technology in the preparation of jointed rock sample[J]. Railway Investigation and Surveying, 2019, 45(3): 70−74.

[13] FAN X, LI K, LAI H, et al. Experimental and numerical study of the failure behavior of intermittent rock joints subjected to direct shear load[J]. Advances in Civil Engineering, 2018: 1−19.

[14] 刘远明, 夏才初. 非贯通节理岩体直剪贯通模型和强度研究[J]. 岩土工程学报, 2006, 28(10): 1242−1247. LIU Yuanming, XIA Caichu.Study on models and strength behavior of rock mass containing discontinuous joints in direct shear[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(10): 1242−1247.

[15] 刘远明. 基于直剪试验的非贯通节理岩体扩展贯通研究[D]. 上海: 同济大学, 2007. LIU Yuanming. Study on failure models and strength of rock mass containing discontinuous joints in direct shear[D]. Shanghai: Tongji University, 2017.

[16] 曹平, 范祥, 蒲成志, 等. 节理剪切试验及其表面形貌特征变化分析[J]. 岩石力学与工程学报, 2011, 30(3): 480−485. CAO Ping, FAN Xiang, PU Chengzhi, et al. Shear test of joint and analysis of morphology characteristic evolution of joint surface[J].Chinese Journal of Rock Mechanics and Engineering, 2011, 30(3): 480−485.

Study on shear failure characteristics of non-coplanar combination joints

CUI Zhimeng1, FAN Xiang1, 2, XIE Yongli1, 2

(1. School of Highway, Chang’an University, Xi’an 710064, China;2. Key Laboratory of Highway Bridges and Tunnels of Shaanxi Province, Chang’an University, Xi’an 710064, China)

To explore the failure law of non-coplanar combination joints under shear load, the laboratory test and numerical calculation methods were used to establish the samples and numerical models of combined joints of the different angles respectively. And those tests under the same load and shear rate test were carried out. Then, the shear results, shear stress curves and micro-cracks of different angle joints were compared and analyzed by the combination of test and numerical methods. At the same time, the micro-crack generation process, the relationship between the combined joint angles of different samples and peak value and residual shear stresses were analyzed separately. The results are given as follows: 1) The transfixion mode of the adjacent combined joint was related to the angle of the combined joints. When the angle was less than or equal to 90°, the transfixion of the adjacent combined joint abode by the principle of proximity; when the angle was greater than 90°, the right end of the crack in a joint intersection that is moved down and finally reached the lower tip. 2) With the increase of the angle, the damage types of the micro-cracks were mainly changed from shear failure to shear-tension damage. Moreover, after the transfixion of combined joint with larger angles, secondary cracks dominated by tensile failure were produced. 3) The peak value of the shear stress curve is negatively correlated with the residual value. The peak shear stress is positively correlated with the angle of the combined joint and the residual stress is negatively correlated.

combined joint; direct shear; the angle of the combined joint; micro-cracks

TU45

A

1672 − 7029(2020)06 − 1411 − 11

10.19713/j.cnki.43−1423/u.T20190754

2019−08−29

国家自然科学青年基金资助项目(41807241)；陕西省自然科学基础研究计划资助项目(2018JQ4015)；浙江省交通运输厅科技计划资助项目(2016019，2019043)

范祥(1986−)，男，四川大竹人，副教授，从事岩体力学与隧道工程研究；E−mail：fanxiang224@126.com

(编辑 涂鹏)