扣件失效对高速列车−无砟轨道−桥梁系统垂向振动响应的影响

周钦悦，刘林芽，龚凯，秦佳良

扣件失效对高速列车−无砟轨道−桥梁系统垂向振动响应的影响

周钦悦，刘林芽，龚凯，秦佳良

(华东交通大学 铁路环境振动与噪声教育部工程研究中心，江西 南昌 330013)

采用动柔度思想，通过建立高速列车−无砟轨道−桥梁系统垂向耦合频域分析模型来求解在单个或连续多个扣件失效下无砟轨道-桥梁系统的动柔度幅值、相位和纵向衰减率，对比分析无扣件失效、单个扣件失效及连续扣件失效等工况对系统在较宽频范围内动力学响应的影响规律。研究结果表明：无砟轨道结构其支撑的连续性在扣件失效下遭到破坏，钢轨、轨道板、底座层和桥梁的动力学响应增量明显；随着扣件失效数目的增多，各结构的动柔度幅值增长明显，其最大主频前移；由于扣件失效造成钢轨纵向衰减率在较高频段时相对减弱，且相位角提前出现跃升现象；轮轨接触力最大幅值由于扣件失效而略微降低，在车体激励下的钢轨加速度整体向低频移动；计算结果显示，扣件连续失效对系统频域下振动响应影响明显，严重影响桥上无砟轨道几何形位，对行车安全形成一定隐患。

高速铁路；频域分析；动柔度法；扣件失效；耦合振动

随着国民经济不断提升，高速铁路发展势头迅猛。截止2018年12月，我国高铁里程已经超过2.5万km，且每年都有数千公里的新增线路。在已开通运营的300~350 km/h高速铁路线路中，京津、武广等主干线路的桥梁部分占比在67%左右[1]。扣件作为重要部件,是高速铁路轨道结构中钢轨与无砟轨道板的紧密连接部[2−4]。然而，随着列车行车速度的提高、列车开行次数的增多，无砟轨道服役状态逐渐下滑，其中扣件松脱、失效等病害日益严重，甚至对高速列车行车安全构成威胁[5−7]。对于扣件失效，国内外学者已开展了一定程度的研究，如：Smutny[8]为研究扣件在频域方面的疲劳伤损机理，针对其时频相互响应关系进行分析，得到了钢轨扣件动态响应关系；Kaewunruen等[9]通过建立有限元模型，用于分析轨枕产生间隙时，轨枕垂向振动模态情况。翁长根等[10]根据弹性系统动力学总势能不变值理论和“对号入座”法则，建立了时域下扣件失效时整车垂向振动分析模型；朱剑月[11]采用缩尺模型测试了不同车速下连续扣件失效对轮轨系统动态响应情况；肖新标等[12]建立车轨耦合系统，分析了时域下扣件失效对列车脱轨的影响；刘学毅等[13]通过有限元软件建立了时域车轨耦合模型，分析了不同组合扣件刚度突变对钢轨振动响应的影响。然而，上述研究主要是扣件失效等对车−轨系统时域下的分析，而关于扣件失效对车−轨−桥系统频域内的影响研究较少。且扣件失效对钢轨结构的振动会产生较大影响，由于钢轨属于高频振动结构，现有时域求解在计算高频振动时需要通过设置较小的积分步长来获取结果，其步骤繁琐，计算耗时长，而动柔度法直接通过建立车−轨−桥频域计算模型，获取力和位移间的关系，相应数值分析更为准确、迅速[14−15]。该方法在扣件失效对车轨桥频域下垂向耦合动力学响应的影响却鲜有研究。为深入研究车轨桥在扣件失效下，其频域内动力响应的变化情况，运用动柔度法，建立高速列车−无砟轨道−桥梁系统垂向耦合动力学频域模型。分析其相互作用系统的动力学特性，为铁路系统相关部门在日常管理维护时提供相关数据参考。

1 高速铁路车辆−无砟轨道−桥梁系统垂向耦合动力学频域模型

将车辆简化为多刚体系统，继而推导出车体动柔度，钢轨简化为无限长Timoshenko梁、轨道板等简化为自由−自由Euler-Bernoulli梁、桥梁简化为简支Euler梁，扣件系统、CA砂浆层及底座层看作线性弹性阻尼单元[14−15]，模型如图1所示。

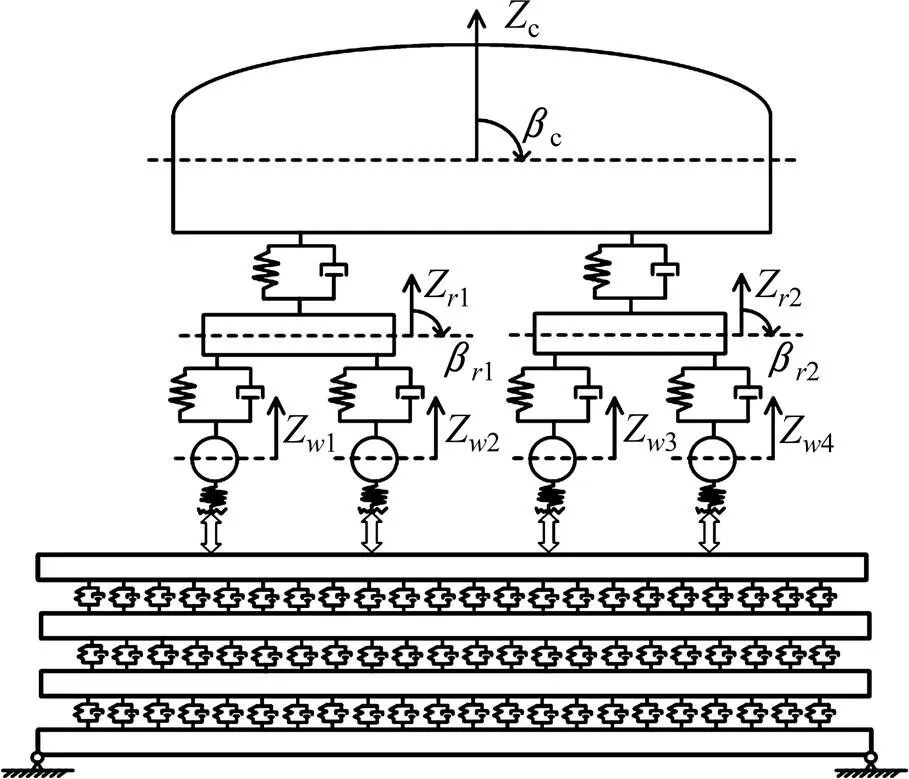
图1 车辆−无砟轨道−桥梁频域分析模型

1.1 车辆模型

采用国内常见的CRH3型高速列车进行分析，简化为10自由度单节车体模型，仅考虑车体和转向架的沉浮和点头，以及轮对的沉浮。高速列车的振动微分方程为：

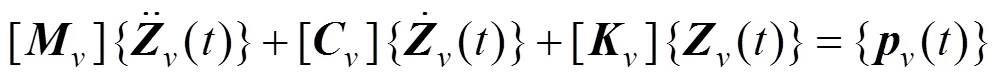
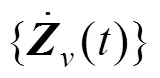
通过线性Hertz接触弹簧形式模拟轮轨处动态作用力相互耦合[16]，轮轨垂向力由钢轨表面的不平顺的相对位移所激励产生,其轨道不平顺所引起的垂向轮轨动态力为谐荷载，该谐响应荷载激扰下车体振动为简谐振动，带入单节高速列车振动微分方程中，得出车体的振动幅值关系式：

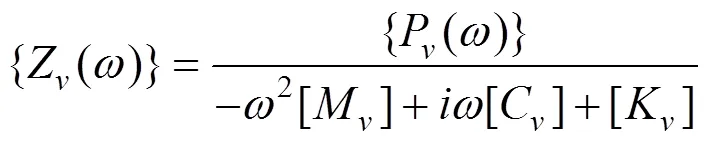
根据单节列车只考虑4个轮对和对应的轮轨垂向力可得：

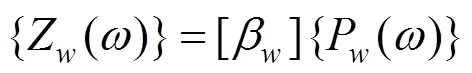
1.2 无砟轨道−桥梁模型

建立无砟轨道−桥梁垂向耦合振动分析模型时，将钢轨简化为无限长Timoshenko梁，考虑垂向和截面转角自由度[17−18]。钢轨的荷载考虑上部车轮的激励荷载以及下部扣件的支撑荷载，动柔度函数可表示为：

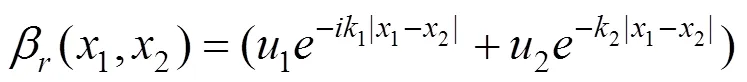
式中：(1,2)表示在钢轨上2处施加单位谐荷载在1处引起的位移；1，2，1和2分别为与钢轨参数有关的系数[3]。

钢轨承受车辆轮对的荷载以及扣件荷载，其频域内的振动位移表达式为：

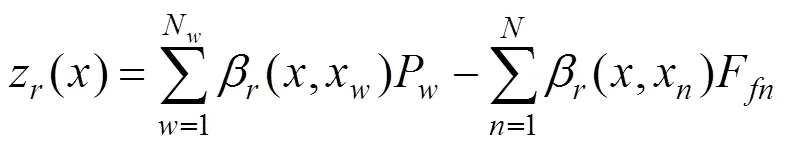
式中：P为第个轮对在钢轨上x处施加在钢轨上的轮轨垂向作用力；N为轮对的数量；F为第钢轨扣件施加到钢轨上x处的扣件反力，为一根钢轨下钢轨扣件的数量。

轨道板模型简化为有限长度“自由−自由”边界，视作Euler-Bernoulli梁进行计算，其在频域内的振动位移表达式为：

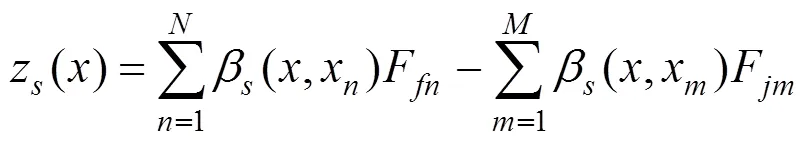
底座层的频域内振动位移表达式为：

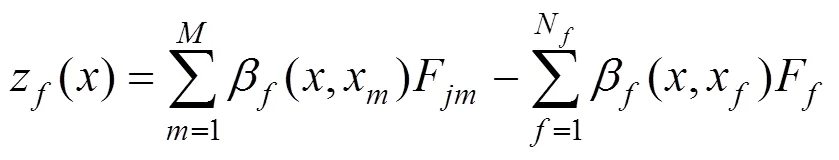
选用简支Euler梁模拟高架桥梁，考虑垂向运动自由度。将桥墩视为刚体，即桥梁支座的一端与桥墩是固定衔接的。桥梁在频域内的振动位移表达式为：

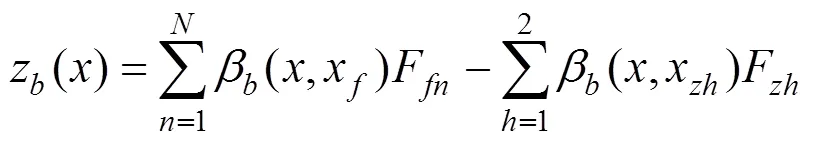
式中：F为第个桥梁支座施加到桥梁上x处的支座反力。

上述建立的子系统，其各结构相互的弹性力F，F，F和F应用下式进行计算：

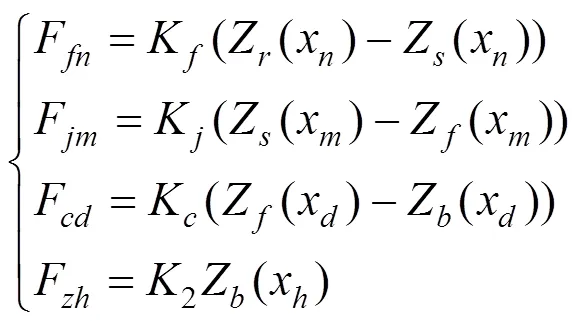
式中：K，K，K和K为连接各部分的弹簧复刚度。

通过联立式(5)，(6)，(7)，(8)和(9)可得矩阵 形式：

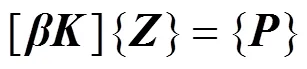
式中：[]主要由无砟轨道−桥梁结构对应的动柔度乘以复刚度组成；{}由待求解的无砟轨道−桥梁结构的位移组成；{}为荷载矩阵。通过该式可求得车体处于桥上某位置时，无砟轨道−桥梁子系统频域位移动力响应。

2 扣件失效对系统动力学响应的影响

2.1 模型计算参数

高铁车辆采用我国常见的CRH3型车辆进行计算，高架桥梁为我国高铁线路莞惠深城际设计中常见的单线30 m简支箱梁桥, 轨道板选择桥梁上适用的CRTS-Ⅱ型，结构参数如表1所示。

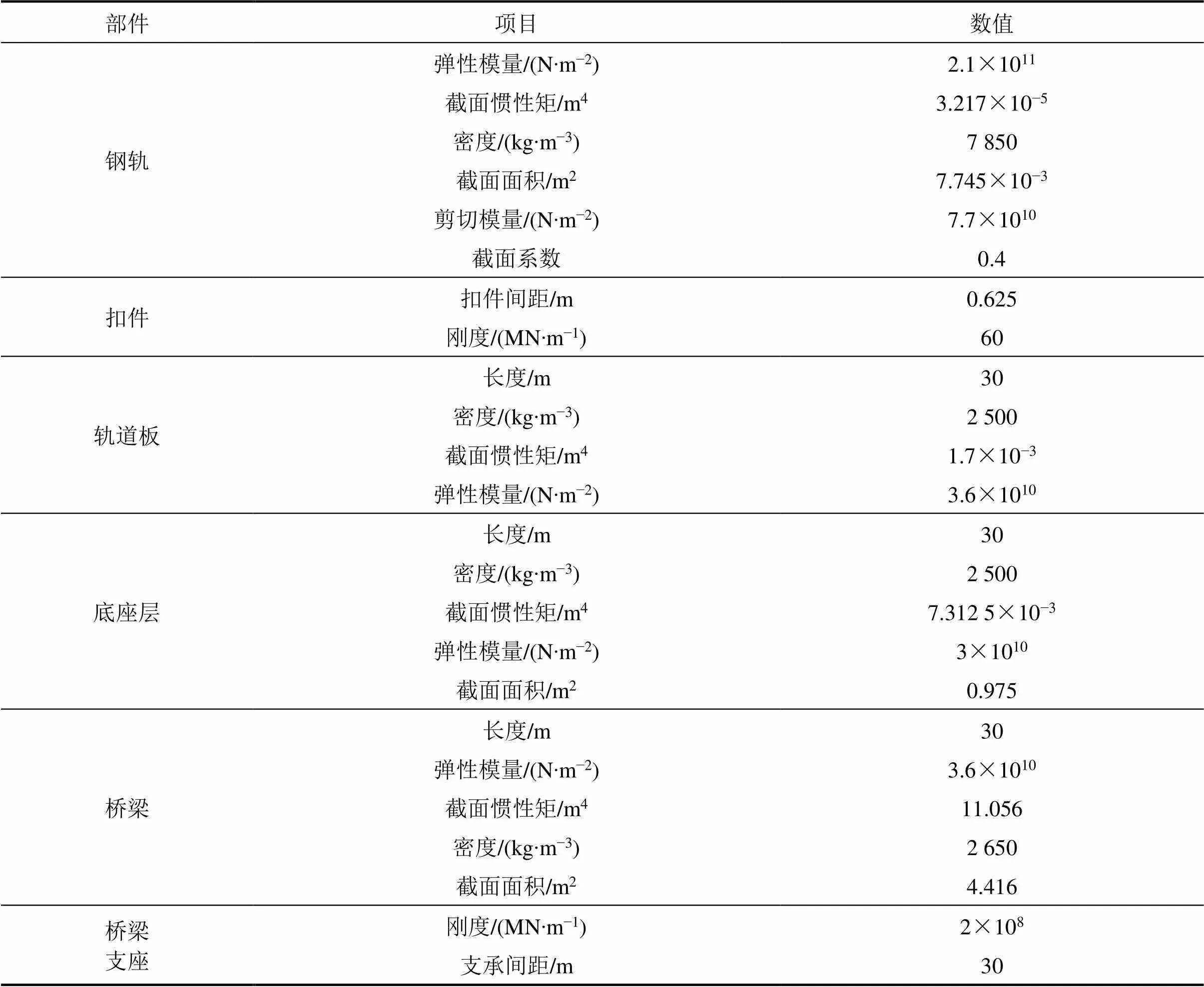
表1 轨道桥梁计算参数

扣件失效的相关特征通常表现为钢轨悬空，从激励类型而言，扣件失效本质上是轨道垂向刚度不平顺。在分析时考虑扣件完全失效，即该处轨道板对钢轨的垂向约束极大减弱，失效处扣件的复合刚度K=0。通过设定的3种计算工况来改变失效扣件所在位置来模拟，具体计算工况见图2。

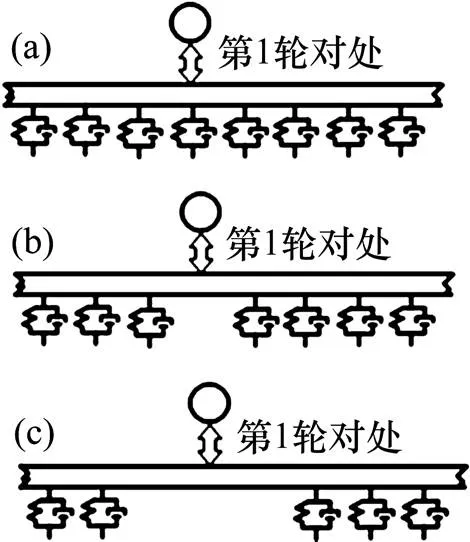
(a) 无扣件失效；(b) 单个扣件失效；(c) 连续(3个)扣件失效

2.2 动柔度特性分析

应用该模型，在钢轨上施加单位简谐荷载作为激励，通过求解无砟轨道−桥梁子系统的动柔度矩阵，在一定程度上反映系统的动力学特性。现将无扣件失效下与单个扣件失效，以及连续扣件失效共3组情况，对无砟轨道−桥梁垂向耦合模型各子系统动柔度的影响一一相互比照，直观分析这3种工况对无砟轨道−桥梁相互作简谐荷载用系统的影响程度。

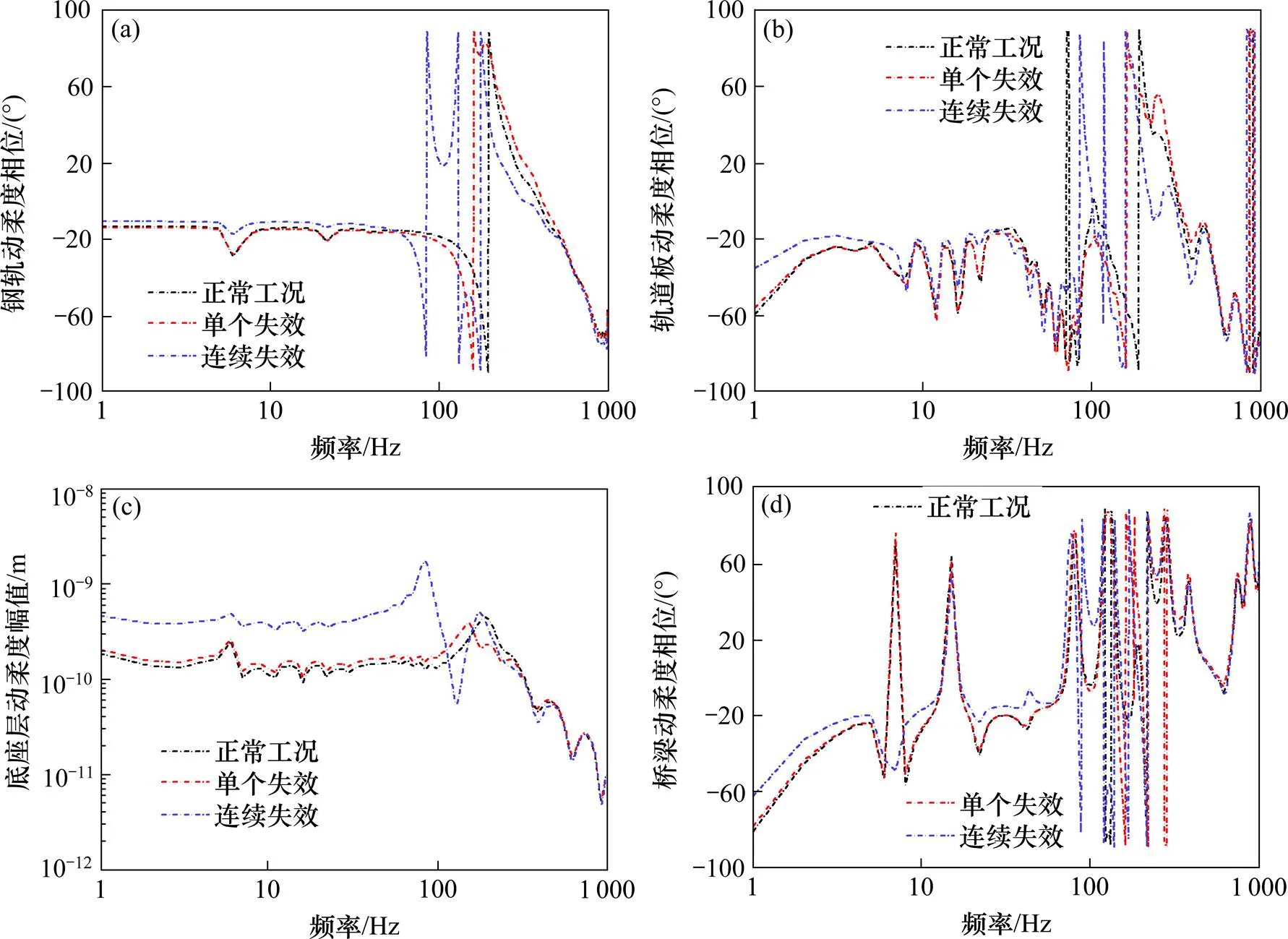
在预设的第1轮对接触点处施加垂向单位简谐荷载，以1 Hz为计算步长，在1~1 000 Hz的频率范围内得出无砟轨道−桥梁相互作用系统各结构的动柔度幅值如图3所示。

从图3可知，由于扣件失效，造成轨道结构刚度降低，致使扣件连续失效下的各结构动柔度幅值上升明显。正常工况下，其在193 Hz左右为最大峰值，单个扣件失效下，其峰值频率相对与正常工况下前移了40 Hz；扣件失效造成钢轨结构支撑减弱，当受到上部荷载时，振动响应更加剧烈，在连续扣件失效下，钢轨动柔度幅值的峰值比正常工况下跃升了310.8%；单个扣件失效使得轨道板在1~171 Hz左右动柔度幅值升高，连续扣件失效在1~199 Hz左右的动柔度幅值升高，在之后的频段趋于缓和；底座层在526 Hz后走势相近，连续扣件失效下的最大峰值相较于正常工况增大285.1%；桥梁结构3种工况的最大峰值分别在211，144和86 Hz，扣件失效下的最大主频前移明显。

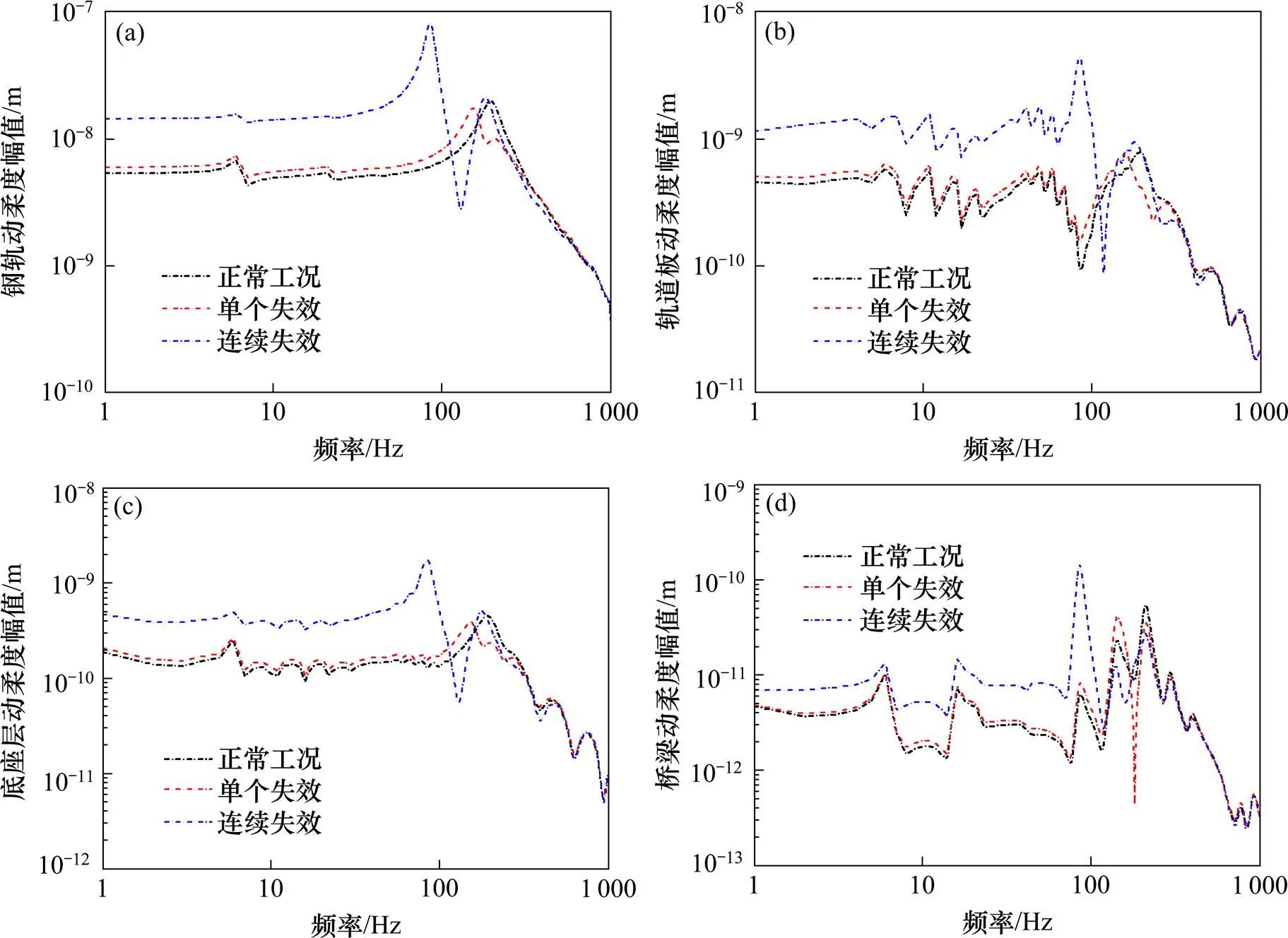
(a) 钢轨；(b) 轨道板；(c) 底座层；(d) 桥梁

图4反映出扣件失效造成钢轨相位角突变到正值的主频前移，且扣件失效数目越多，前移量越大。在84 Hz前正常工况相位角相对最大，之后在85~130 Hz连续失效下的钢轨相位角突变为最大，161 Hz是单个失效下突变最大频率，在556 Hz后3种工况的走势趋近相同；轨道板相位角相对钢轨减小较快，在71 Hz处正常工况相位角发生突变，而连续失效下相位角在161~328 Hz连续出现3个大于0的峰值，表明连续扣件失效造成相位角在中低频一定区间内持续大于0，3种工况在接近850 Hz处开始振荡剧烈；底座层在84 Hz前正常工况相位角最大，桥梁处相位角在7 Hz处，正常工况和单个扣件失效下的相位角都跃升至正值，而扣件连续失效造成桥梁相位角在此处反而降至谷底，在14 Hz处3种工况都跳跃到正值，在68 Hz处连续扣件失效率先振荡，此后3种工况都出现剧烈振荡现象。

系统各部分结构通过振动衰减率来反映结构上随着距离激励点距离的改变，其纵向振动衰减的特性。

衰减率定义为：

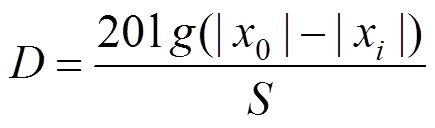
式中：0为单位简谐荷载处下该部分的振动位移，x为距离单位简谐荷载处该部分的振动位移。

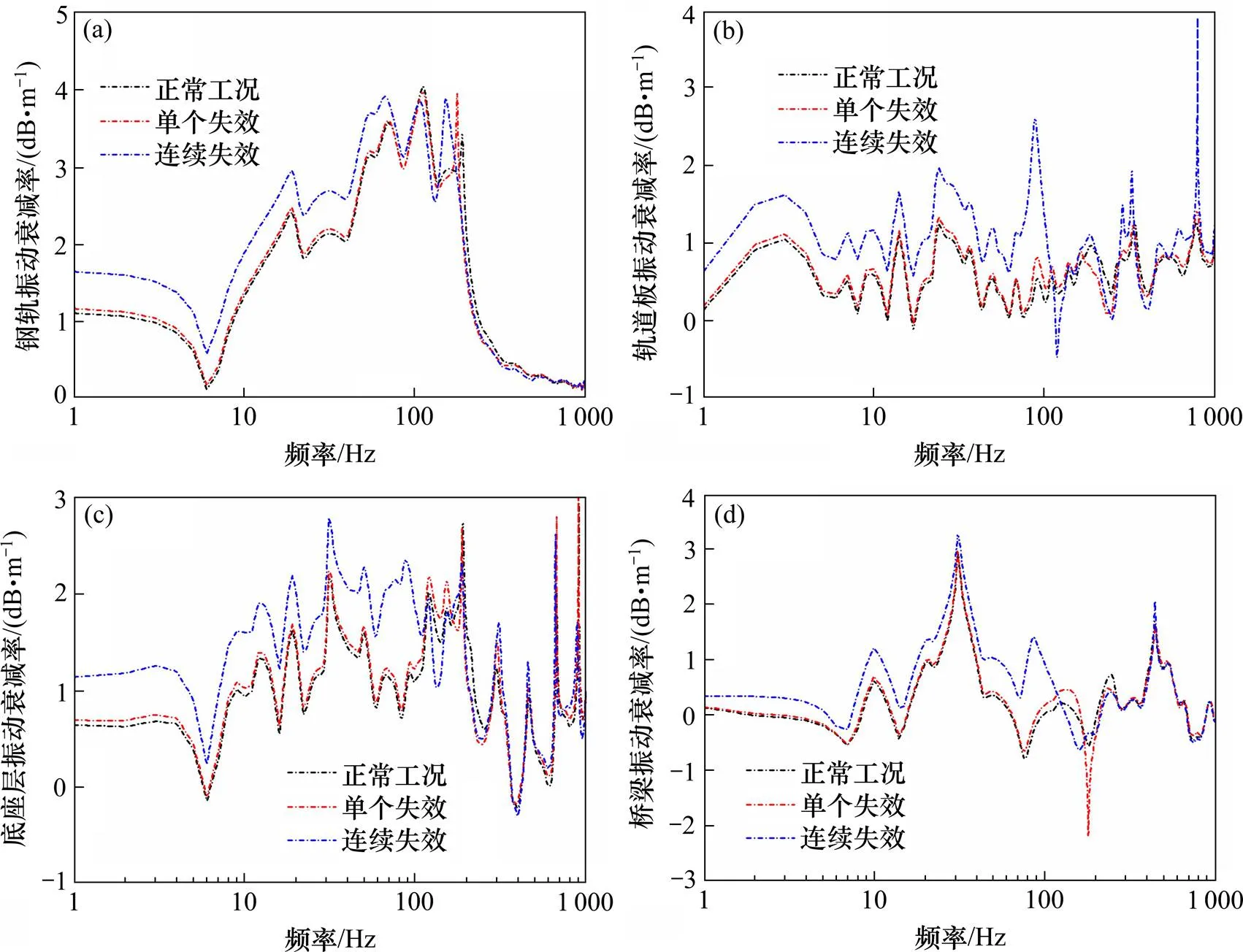
在钢轨预设的第1轮轨处施加单位简谐荷载，分别获取在钢轨、轨道板、底座层和桥梁上跨中位置处的振动幅值，如图5示，分析振动在系统中的纵向衰减情况。

从图5可知，扣件失效造成各部件的纵向衰减峰值增多，但是其主频变化不大，且随着扣件失效数目增多，其峰值更大；在104 Hz前连续扣件失效下的钢轨衰减始终相对较大，在112 Hz处正常工况下的钢轨衰减最大，在155 Hz左右三者衰减滑入谷底，且钢轨随着扣件失效数目的增多，其高频衰减率减小；连续失效下的轨道板、底座层及桥梁在110 Hz前衰减始终较大，反映出随着扣件失效数目的增长，轨道结构在受到轮对激励时，其振动更易聚集在扣件失效处附近，对邻近轨道造成更大影响。

(a) 钢轨；(b) 轨道板；(c) 底座层；(d) 桥梁

(a) 钢轨；(b) 轨道板；(c) 底座层；(d) 桥梁

3 谱激励响应分析

利用该车−轨−桥系统，采用现在我国高铁列车常见的行车速度=300 km/h，计算车−轨−桥系统各子系统动力学频域响应。图6为车体在不平顺谱[16]的激励下，3种工况下车体第1轮对垂向轮轨相互作用力幅值。

从图6可以看出，由于扣件失效，造成轮轨作用力幅值主频前移，且钢轨缺少支承，导致相应峰值减小。在25 Hz处连续扣件失效下的轮轨垂向作用力达到峰值，比正常工况下前移了18 Hz，在140~670 Hz内，随着频率的增长，3种工况下的轮轨作用力幅值呈上浮趋势；当大于670 Hz后，随着频率的增长，3种工况下的轮轨作用力幅值呈降低趋势。

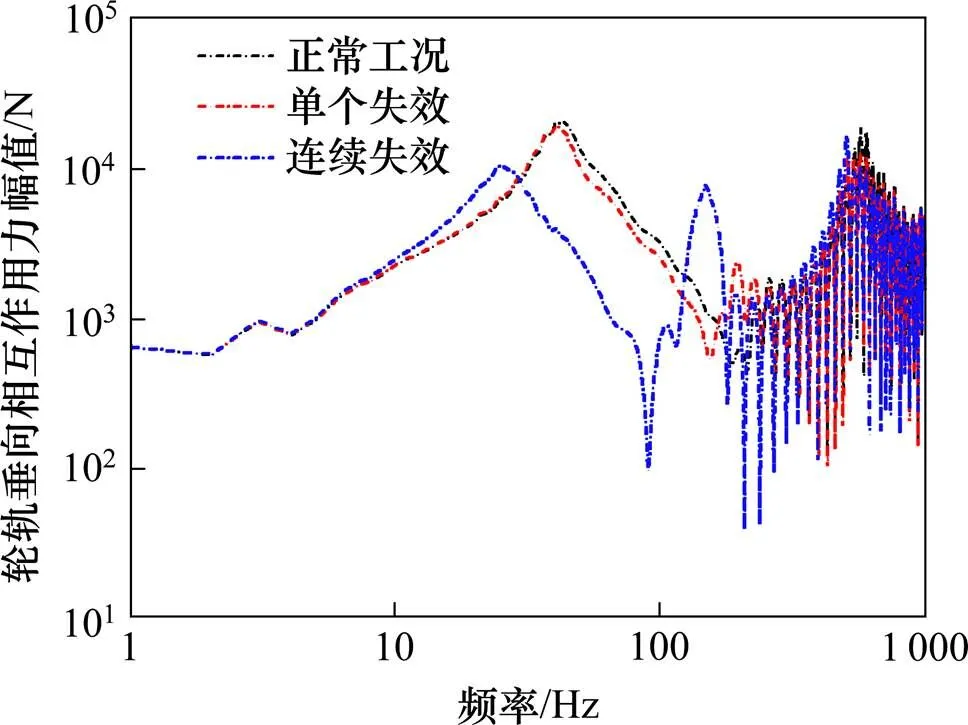
图6 轮轨垂向相互作用力幅值

(a) 钢轨；(b) 轨道板；(c) 底座层；(d) 桥梁

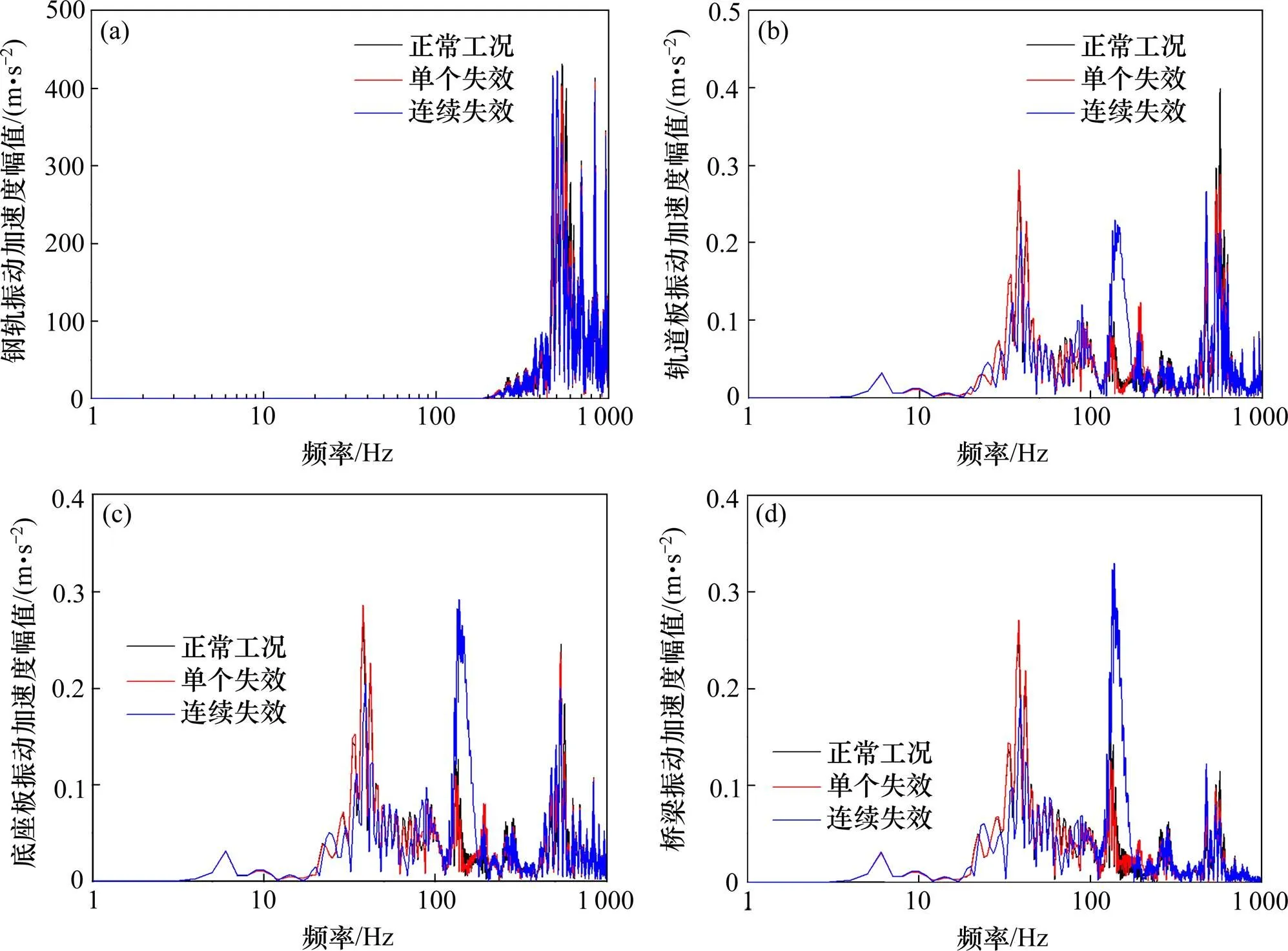
图7中，在车体运行时速300 km/h时，3种工况在不平顺激励下的跨中位置处无砟轨道−桥梁相互作用系统的响应情况，钢轨在低频段的振动响应很小，连续扣件失效下的钢轨振动在462 Hz处最先开始跃升，3种工况都在一阶pinned-pinned频率振动加速度达到最高位；轨道板、底座层和桥梁在低频处大致趋近，在133~210 Hz范围内，连续扣件失效对结构振动影响显著，其振动加速度大于另外2种工况；在29~55 Hz范围内，单个扣件失效造成3种结构的振动加速度显著增大，反映出随着扣件失效数目的增加，轨道结构整体振动都在增强，极易造成轨道结构进一步损坏，影响行车安全。

4 结论

1) 高速铁路桥上扣件失效，会导致结构的支撑连续性遭到破坏，进而引起结构的刚度变化，加剧轮轨间相互作用，对轨道结构振动影响较大，特别是连续扣件失效时，各动力学特性指标增大幅度明显，其中钢轨动柔度幅值相对正常工况跃升了310.8%。

2) 当模拟时速300 km/h车体位于桥梁跨中位置时，由于扣件失效造成钢轨支承减弱，轮轨作用力幅值降低，但连续扣件失效在25 Hz和148 Hz处出现2个明显峰值；钢轨振动加速度由于扣件失效提前开始跃升，在133~210 Hz范围内，连续扣件失效对结构振动影响显著，峰值处相对正常工况增大111.25%，其振动加速度明显持续大于另外2种工况。

3) 应用动柔度思想建立起车−轨−桥系统频域模型，获得的动力学特性反映，随着扣件失效数目的增多，钢轨在频域下的振动响应表现的更加剧烈。

[1] 杨宜谦, 姚京川, 孟鑫, 等. 时速300~350 km高速铁路桥梁动力性能试验研究[J]. 中国铁道科学, 2013, 34(3): 14−19. YANG Yiqian, YAO Jingchuan, MENG Xin, et al. Experimental study on dynamic performance of high- speed railway bridges with speeds of 300~350 km/h[J]. China Railway Science, 2013, 34(3): 14−19.

[2] 施何瑛, 王安斌, 高晓刚. 高速铁路扣件弹条性能分析及频响特性研究[J]. 噪声与振动控制, 2019, 39(1): 156−159. SHI Heying, WANG Anbin, GAO Xiaogang. Performance analysis and frequency response characteristics of fasteners for high-speed railway[J]. Noise and Vibration Control, 2019, 39(1): 156−159.

[3] 张燕, 卢沛君. 扣件刚度对车辆−轨道−桥梁耦合系统频率响应的影响[J]. 铁道科学与工程学报, 2018, 15(12): 3141−3147. ZHANG Yan, LU Peijun. The effect of fastener stiffness on frequency response of vehicle-track-bridge coupling system[J]. Journal of Railway Science and Engineering, 2018, 15(12): 3141−3147.

[4] LUO Y, LIU Y, YIN H P. Numerical investigation of nonlinear properties of a rubber absorber in rail fastening systems[J]. International Journal of Mechanical Sciences, 2013, 69(4): 107−113.

[5] 仲伟秋, 逯云芳, 赵岩, 等. 扣件失效下轨道结构的随机振动分析[J]. 低温建筑技术, 2015, 13(4): 35−37. ZHONG Weiqiu, QU Yunfang, ZHAO Yan, et al. Random vibration analysis of track structures under fastener failure[J]. Low Temperature Building Technology, 2015, 13(4): 35−37.

[6] 肖宏, 马春生, 郭骁, 等. E型扣件弹条断裂原因频谱分析[J]. 同济大学学报(自然科学版), 2017, 45(7): 1000−1008. XIAO Hong, MA Chunsheng, GUO Xiao, et al. Frequency spectrum analysis of fracture reasons of E-fastener spring bar[J]. Journal of Tongji University (Natural Science Edition), 2017, 45(7): 1000−1008.

[7] 代先星, 丁世海, 阳恩慧, 等. 铁路扣件弹条伤损自动检测系统研发与验证[J]. 铁道科学与工程学报, 2018, 15(10): 30−38. DAI Xianxing, DING Shihai, YANG Enhui, et al. Development and validation of automatic detection system for bullet-bar damage of railway fasteners[J]. Journal of Railway Science and Engineering, 2018, 15(10): 30−38.

[8] Smutny J. Measurement and analysis of dynamic and acoustic parameters of rail fastening[J]. Ndt & E International, 2004, 37(2): 119−129.

[9] Kaewunruen S, Remennikov A M. Investigation of free vibrations of voided concrete sleepers in railway track system[J]. Proceedings of the Institution of Mechanical Engineers, 2007, 221(4): 495−507.

[10] 翁长根, 赫丹, 王阳, 等. 扣件失效对城市轨道交通列车−浮置板式轨道系统竖向振动响应的影响[J]. 铁道科学与工程学报, 2008, 5(2): 29−33. WENG Changgen, HE Dan, WANG Yang, et al. Effect of fastener failure on vertical vibration response of train-floating slab track system in urban rail transit[J]. Journal of Railway Science and Engineering, 2008, 5(2): 29−33.

[11] 朱剑月. 轨下扣件支承失效对轨道结构动力性能的影响[J]. 振动工程学报, 2011, 24(2): 158−163. ZHU Jianyue. Effect of failure of under track fastener support on dynamic performance of track structure[J]. Journal of Vibration Engineering, 2011, 24(2): 158−163.

[12] 肖新标, 金学松, 温泽峰. 钢轨扣件失效对列车动态脱轨的影响[J]. 交通运输工程学报, 2006, 6(1): 10−15. XIAO Xinbiao, JIN Xuesong, WEN Zefeng. Effect of rail fastener failure on train dynamic derailment[J]. Journal of Transportation Engineering, 2006, 6(1): 10−15.

[13] 刘学毅, 张重王, 万章博. 无砟轨道扣件刚度突变对高速列车动力的影响[J]. 铁道工程学报, 2014, 31(9): 53−58. LIU Xueyi, ZHANG Chongwang, WAN Zhangbo. The impact of sudden change in stiffness of fasteners of ballastless track on the dynamics of high-speed trains[J]. Journal of Railway Engineering, 2014, 31(9): 53−58.

[14] LIU Linya, SONG Rui, ZHOU Yunlai, et al. Noise and vibration mitigation performance of damping pad under CRTS-III ballastless track in high speed rail viaduct[J]. KSCE Journal of Civil Engineering, 2019, 23(8): 3525− 3534.

[15] LIU Linya, QIN Jialiang, LIU Quanmin, et al. Spectral analysis of train-rail-bridge coupling system considering frequency-dependent stiffness of rail fastening systems[J]. Journal of Marine Science and Technology, 2019, 27(2): 114−122.

[16] 宋瑞, 刘林芽, 徐斌, 等. 基于动柔度法的轨道高架桥橡胶垫减振性能研究[J]. 噪声与振动控制, 2018, 38(3): 141−145. SONG Rui, LIU Linya, XU Bin, et al. Study on vibration reduction performance of rubber pads for track viaducts based on dynamic flexibility method[J]. Noise and Vibration Control, 2018, 38(3): 141−145.

[17] SHENG X, LI M, Jones C J C, et al. Using the Fourier-series approach to study interactions between moving wheels and a periodically supported rail[J]. Journal of Sound and Vibration, 2007, 303(3−5): 873− 894.

[18] ZHANG S G, XIAO X B, WEN Z F, et al. Effect of unsupported sleepers on wheel/frail normal load[J]. Soil Dynamics and Earthquake Engineering, 2008, 28(8): 662−673.

Influence of fastener failure on vertical vibration responses of the high-speed train-ballastless track-bridge coupled system

ZHOU Qinyue, LIU Linya, GONG Kai, QIN Jialiang

(Ministry of Education, Engineering Research Center of Railway Environment Vibration and Noise, East China Jiaotong University, Nanchang 330013, China)

Based on the concept of dynamic flexibility, the coupled vertical dynamic frequency domain analysis model of high-speed train-ballastless track-bridge system was established to solve the dynamic flexibility amplitude, phase and longitudinal attenuation rate of ballastless track-bridge system under single or continuous multiple fasteners failures. The influence trends of dynamic responses of the system under the conditions of no fastener failure, single fastener failure and continuous fastener failures were compared and analyzed in a wider frequency range. The results show that the continuity of the support of ballastless track structure is destroyed under the failure of fasteners, and the dynamic response increments of rails, track slabs, supporting layers and bridges are considerable; with the increase of the number of failed fasteners; the dynamic flexibility amplitude of each structure increases obviously, and its maximum principal frequency moves forward; the longitudinal attenuation rate of rails decreases relatively in the high frequency band due to the failure of fasteners, and the dynamic response increments of rails, track slab, supporting layer and bridge are significant. The phase angle jumps ahead of time; the maximum amplitude of wheel-rail contact force decreases slightly due to the failure of fasteners, and the rail acceleration moves to low frequency as a whole under the excitation of the car body; the calculation results show that the continuous failure of fasteners has a significant impact on the vibration responses of the system in the frequency domain, seriously affecting the geometric shape and position of ballastless track on the bridge, thus forming a certain hidden danger to the driving safety.

high-speed railway; frequency analysis; dynamic flexibility method;fastener failure; coupled vibration

U233

A

1672 − 7029(2020)06 −1337 − 09

10.19713/j.cnki.43−1423/u.T20190872

2019−10−08

国家自然科学基金资助项目(51578238，51968025)；江西省自然科学基金重点资助项目(20192ACBL20009)；江西省重点研发计划资助项目(20181BBE50013)

刘林芽(1973−)，男，江西樟树人，教授，博士，从事轨道交通环境振动与噪声研究；E−mail：lly1949@163.com

(编辑 涂鹏)