地震作用下钢筋混凝土柱破坏模式的数值模拟

高 鹏, 王 盖, 刘英南, 高佳琪

(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.同济大学 工程结构性能演化与控制教育部重点实验室,上海 200092)

钢筋混凝土柱作为房屋结构的竖向承重和水平抗力构件,地震中一旦破坏会危及整个结构的安全。钢筋混凝土柱在地震作用下可分为弯曲、弯剪和剪切破坏等形式。表观上来看,弯曲破坏是柱在纵筋屈服后柱经过较大的塑性变形,柱底部混凝土达到极限压应变而被大面积压碎[1]。弯剪破坏是柱纵筋屈服后,经过一段变形后箍筋屈服,而最终发生剪切破坏[2]。剪切破坏是柱在经历短暂弹性变形后出现斜裂缝扩展,箍筋迅速屈服和拉断,斜裂缝贯通截面而破坏[3]。文献[4]使用ANASY软件模拟了钢筋混凝土柱的弯曲和弯剪破坏模式;文献[5]采用ABAQUS模拟了钢筋混凝土柱的剪切黏结破坏形态,模拟中柱混凝土应变分布与试验破坏形态基本相符。

但目前有限元模拟中对钢筋混凝土柱在地震作用下破坏模式的区分还不够细致全面。本文选取某钢混柱在低周反复力作用下的试验,通过软件模拟了柱的破坏过程,并分析了相关参数对柱受力性能的影响,从不同角度区分了柱的不同破坏模式,为柱的抗震研究提供有效依据。

1 钢筋混凝土柱拟静力试验

文献[2]进行了24根钢筋混凝土柱在低周往复荷载作用下的破坏试验。柱尺寸和配筋如图1所示,其中柱混凝土强度等级为C40,纵筋和箍筋的屈服强度分别为365.2、346.9 MPa,箍筋配箍率为0.66%。试验中通过竖向千斤顶施加轴力并保持,在柱侧面用千斤顶施加水平位移实现低周往复加载。开始时位移加载2 mm,以后每级增加4 mm,直至柱破坏。本文选取其试验中的弯曲破坏、弯剪破坏和剪切破坏的钢筋混凝土柱各1根进行模拟验证。其中,弯曲和弯剪破坏柱高H为1 150 mm,轴压比分别为0.2和0.5;剪切破坏柱高H为400 mm,轴压比为0.5。

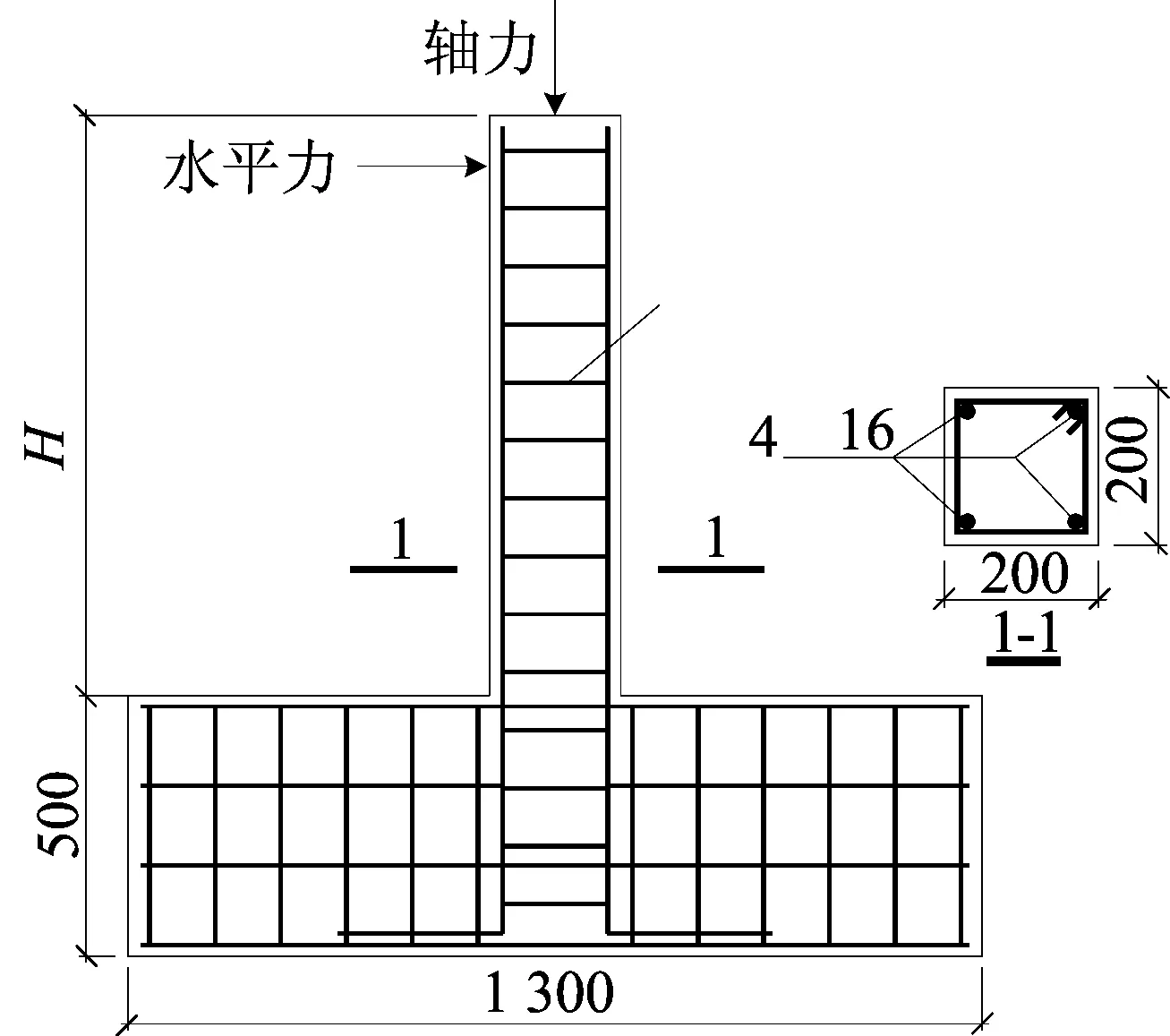
图1 试验柱尺寸和配筋

2 有限元建模与模拟

2.1 单元选择

混凝土采用三维实体单元C3D8R,纵筋和箍筋采用Truss单元T3D2,单元边长为30 mm。模型中未建立纵筋和混凝土的滑移单元,只在纵筋本构模型中综合考虑了钢筋与混凝土之间的黏结滑移和混凝土保护层剥落的情况。

2.2 材料模型

模型中混凝土采用混凝土塑性损伤模型(concrete damaged plasticity, CDP),如图2所示。

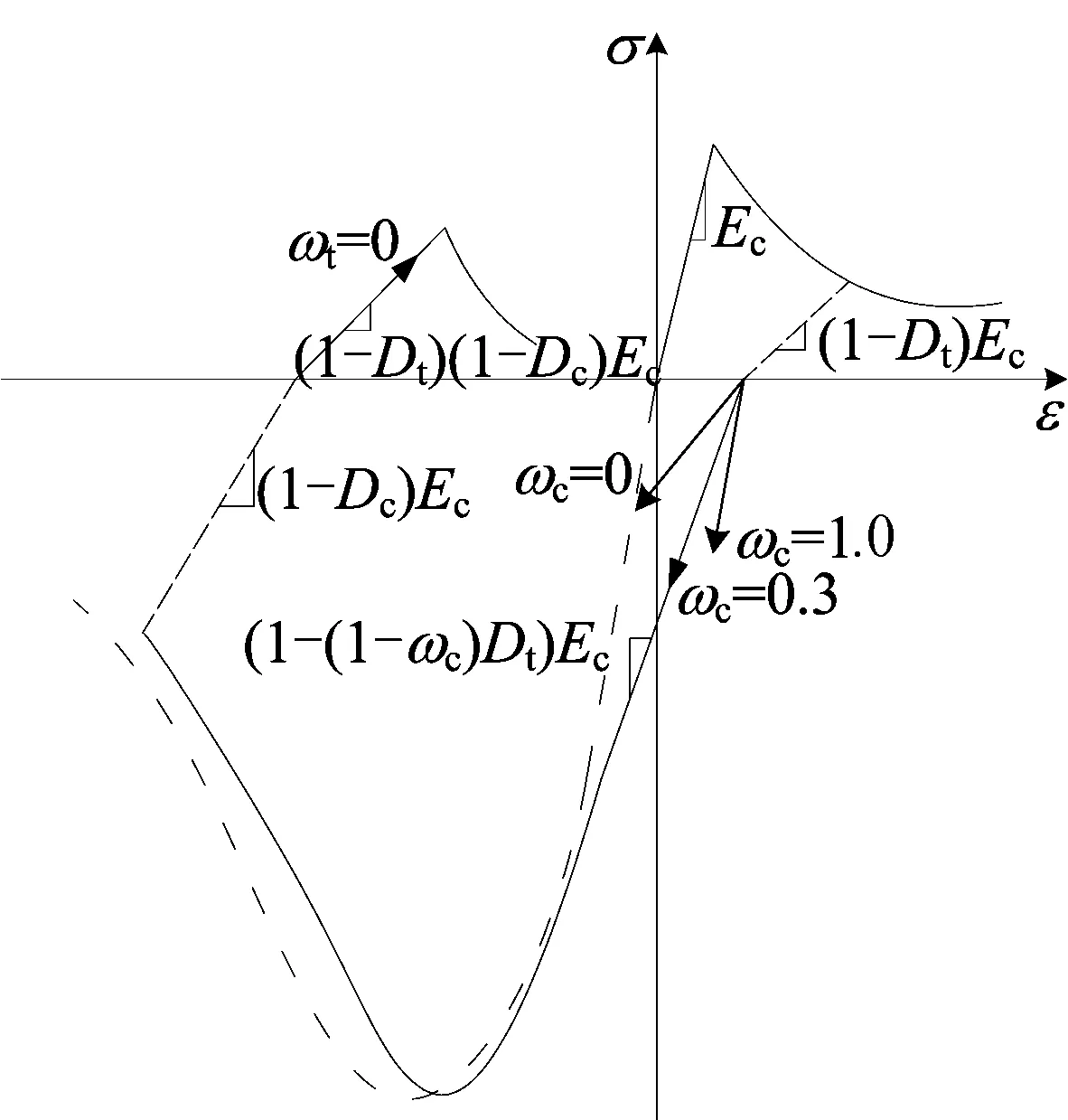
图2 混凝土本构关系

采用文献[6]中的混凝土本构关系。混凝土在达到受拉和受压峰值应力前均不考虑损伤,达到峰值应力后定义受拉和受压损伤因子。根据能量等效性假设[7],即无损材料与损伤材料弹性余能相同,得到混凝土应力σ与弹性模量E、混凝土应变ε和损伤因子D之间的关系σ=(1-D)2E0ε。将公式带入文献[6]的混凝土本构关系中可得:

(1)

其中,d为规范中的混凝土本构的受拉或受压损伤参数。

混凝土受压刚度恢复系数ωc对本构曲线有较大影响[8]。ωc取值为0表示材料刚度不恢复,为1表示刚度完全恢复,本文试算取为0.3;混凝土受拉刚度恢复系数取值为0,如图2所示。

纵筋采用Clough提出的双折线再加载刚度退化滞回本构模型[9]，如图3所示。

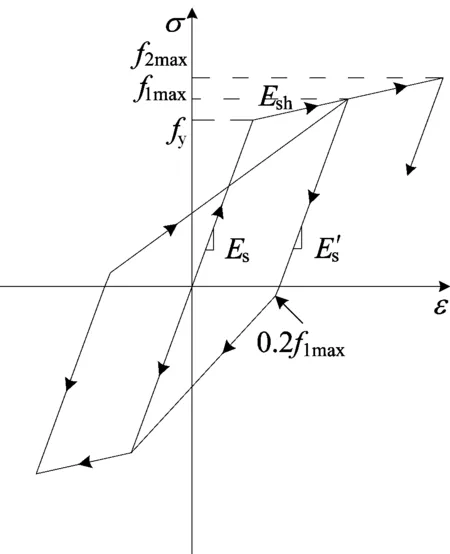
图3 钢筋滞回本构关系

钢筋本构模型通过调用子程序pq-fiber实现。该模型中卸载刚度Es′与加载刚度Es保持一致,硬化刚度Esh取加载刚度的0.01倍。反向再加载时,先按卸载刚度加载至历史最大点对应应力的0.2倍,再指向历史最大点。其他钢筋采用理想弹塑性模型。

模拟中设定柱基座底部平面完全固结,在柱端实施水平位移加载实现低周往复力,加载制度与试验中相同。

2.3 模拟结果

2.3.1 破坏形态对比

因为柱在低周反复作用下混凝土等效塑性应变会不断累积,所以模拟结果中试件破坏形态以混凝土等效塑性应变云图形式给出,如图4所示。

由图4a可知,弯曲破坏试验柱底部100 mm范围内的混凝土被压碎剥落,弯曲水平裂缝主要分布在根部以上的300 mm范围内,并延底部向上数量逐渐减少;模拟柱输出的混凝土等效塑性应变区域也集中于距柱底100 mm范围内,塑性应变分布离开柱根部逐渐减小。

由图4b可知,弯剪破坏柱底部250 mm范围内混凝土保护层剥离,并出现交叉的斜裂缝;模拟柱中可见混凝土等效塑性应变主要分布在距柱底250 mm范围内,柱底两侧等效塑性应变较大,呈X型分布。

由图4c可知,剪切破坏柱出现一条明显的贯穿斜裂缝;模拟柱中混凝土等效塑性应变分布也呈斜向贯穿柱截面。

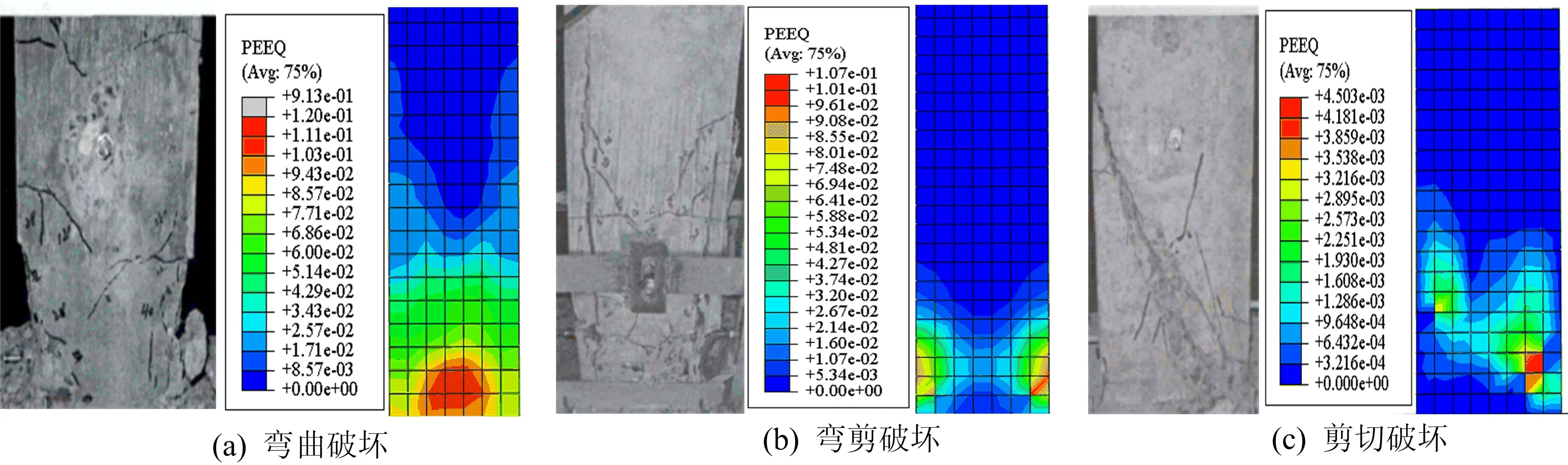
图4 破坏形态对比

由图4中混凝土等效塑性应变分布可见,试验柱和模拟柱破坏形态相符程度较高。

2.3.2 滞回曲线对比

弯曲破坏试验柱的荷载位移滞回曲线形状呈饱满的梭形,滞回环数量多;而弯剪破坏柱的剪切变形比例增大,其曲线中部会出现“捏拢”现像;剪切破坏柱的滞回曲线“捏拢”现象更加明显,滞回环数少[10]。

3种破坏模式下柱荷载位移试验曲线与模拟曲线对比如图5所示,图5中虚线为试验结果,实线为模拟结果,并在曲线上用图例标注不同钢筋屈服位置。

从图5a可以看出,弯曲柱的试验曲线和模拟曲线在形状、峰值荷载和极限位移等方面的特征均吻合较好。

从图5b可以看出,弯剪破坏柱2种曲线的峰值荷载及极限位移吻合较好，但由于模型中未设立钢筋与混凝土之间的滑移界面单元,导致模拟柱刚度退化没有试验柱的明显,模拟柱曲线的“捏拢”效果要略差于试验曲线。

同时,由图5c可见剪切破坏柱的峰值荷载和极限位移的模拟结果略小于试验结果。

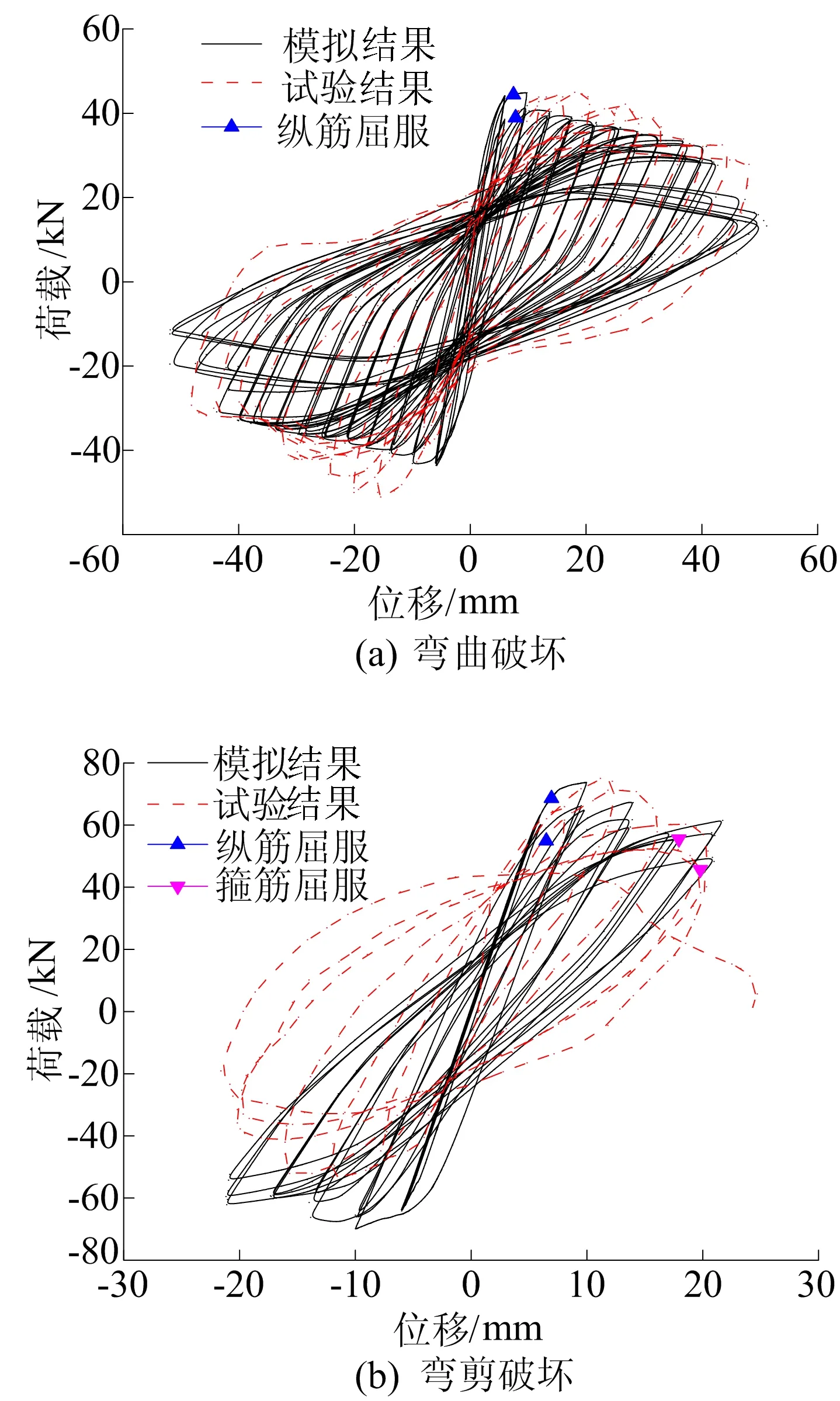
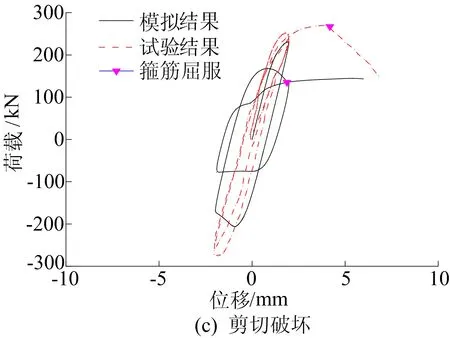
图5 滞回曲线对比

2.3.3 破坏机理对比

在有限元模拟过程中,钢筋和混凝土材料的应力和应变是可观测的,因此柱的3种地震破坏模式可从纵筋与箍筋屈服顺序以及混凝土应变的机理上来判别。钢筋混凝土柱3种地震破坏模式的荷载位移曲线和极限受力状态如图6所示[11],图6中，虚线为抗剪承载力包络线;实线为不同破坏模式下的荷载位移曲线。弯曲破坏柱在纵筋屈服后,继续加载至混凝土达到极限压应变时达到构件极限状态,整个过程中荷载位移曲线位于抗剪承载力包络线下方,箍筋并未屈服。弯剪破坏柱在纵筋屈服后继续加载混凝出现斜裂缝后,截面抗剪承载力下降,经过一段位移后,荷载位移曲线与抗剪承载力包络线相交时箍筋屈服。剪切破坏柱在加载过程中荷载位移曲线与抗剪承载力包络线相交时箍筋屈服,纵筋未屈服。图6分别给出箍筋屈服时弯剪和剪切破坏截面上材料的应力应变状态。由于弯剪和剪切破坏柱在箍筋达到屈服应力后混凝土并未达到极限压应变,因此多数地震试验中对于弯剪和剪切破坏时柱极限状态并无明确的定义。文献[11]以箍筋首次达到屈服作

为柱弯剪和剪切破坏的极限状态。文献[12]认为剪跨比大于2.5的柱在箍筋屈服后,水平荷载降低至0.65倍峰值荷载时达到极限状态。本文采用以上2种方法定义构件的剪切和弯剪破坏。

由图5可知,模拟和试验构件纵筋与箍筋的屈服顺序一致,从破坏机理角度可以分析明确区分出3种破坏模式,并与破坏形态和滞回曲线表现判断一致。综上,所建立的有限元模型可很好地从破坏形态、滞回曲线和破坏机理3个方面区分钢筋混凝土柱地震破坏模式。

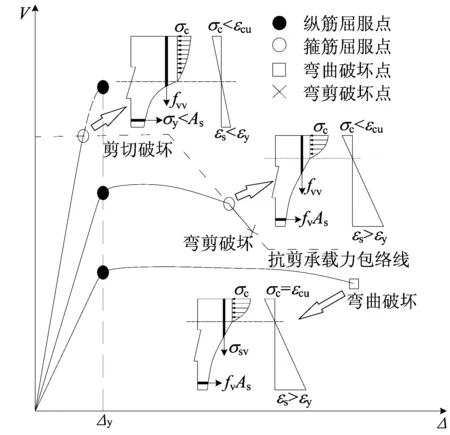
图6 钢筋混凝土柱的3种地震破坏模式机理

3 参数分析

本文设计3组共15根钢筋混凝土柱,探讨轴压比、混凝土强度及配箍率对钢筋混凝土柱在地震作用下的受力性能和破坏模式的影响,试件具体参数见表1所列。

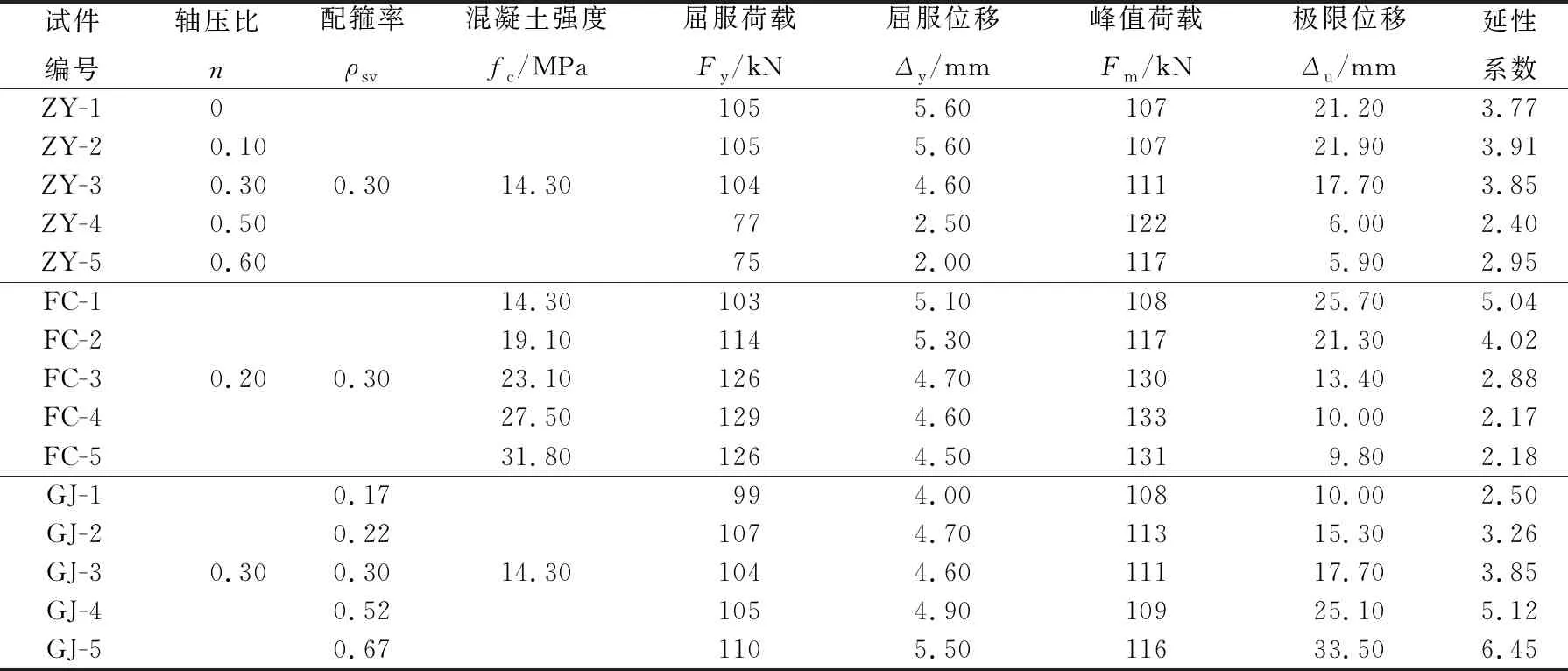
表1 试件参数

试件尺寸及配筋如图7所示。

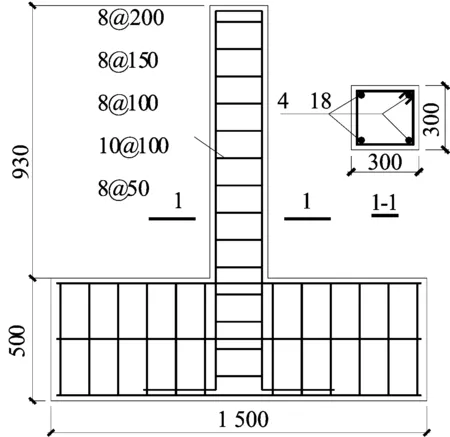
图7 数值分析试件尺寸

混凝土基本强度为14.3 MPa,纵筋屈服强度为360.0 MPa。在模型中通过在柱顶变化轴力大小来取不同轴压比参数(ZY)、变化箍筋直径和间距来取不同配箍率参数(GJ)、混凝土强度(FC)和其他参数取值见表1所列,表1中同时给出了相关模拟结果。

3.1 轴压比

轴压比参数组试件的混凝土等效塑性应变云图如图8所示。

由图8可知，随轴压比增大,混凝土高塑性应变区域逐渐减小,塑性应变由柱底全截面的高应变均匀分布转变为集中于距柱底300 mm范围内两侧的X型分布。

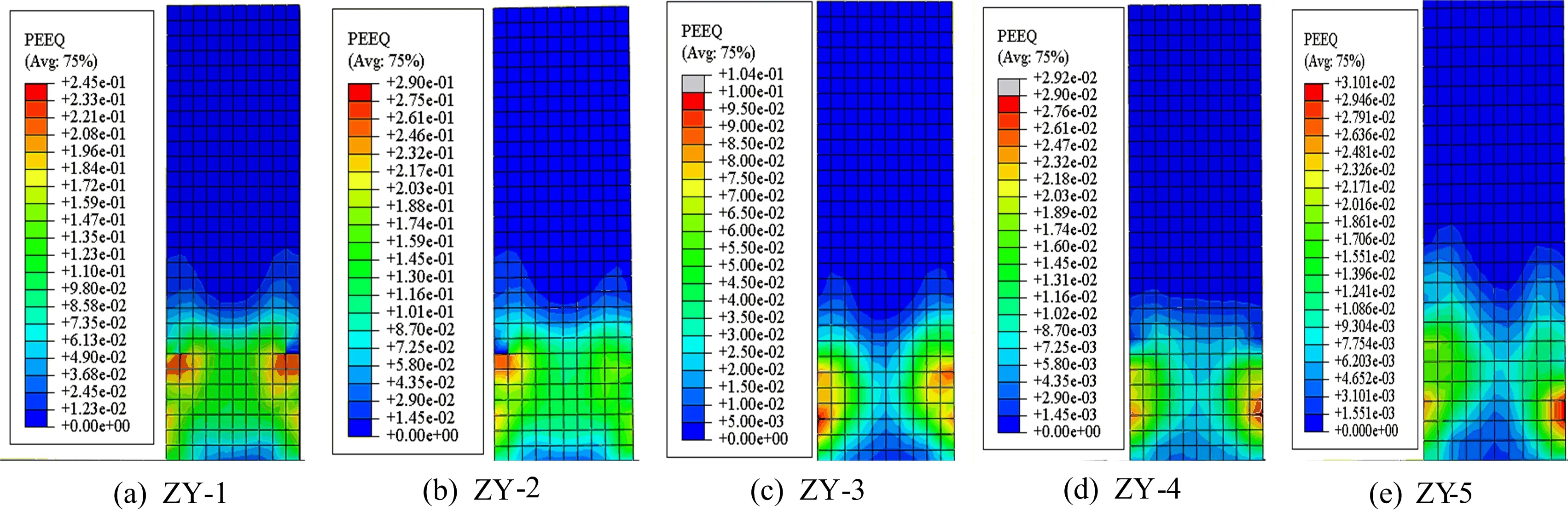
图8 轴压比组试件混凝土等效塑性应变云图

柱的荷载滞回曲线如图9所示,从图9可以看出，轴压比较小的ZY-1和ZY-2柱发生了弯曲破坏,轴压比大于等于0.3的其他柱发生弯剪破坏;且随着轴压比增大,曲线饱满程度降低,滞回环数减少。

由表1可知,在轴压比小于0.5时,随着轴压比增大，构件峰值承载力增大,但轴压比至0.6时峰值承载力反而降低。

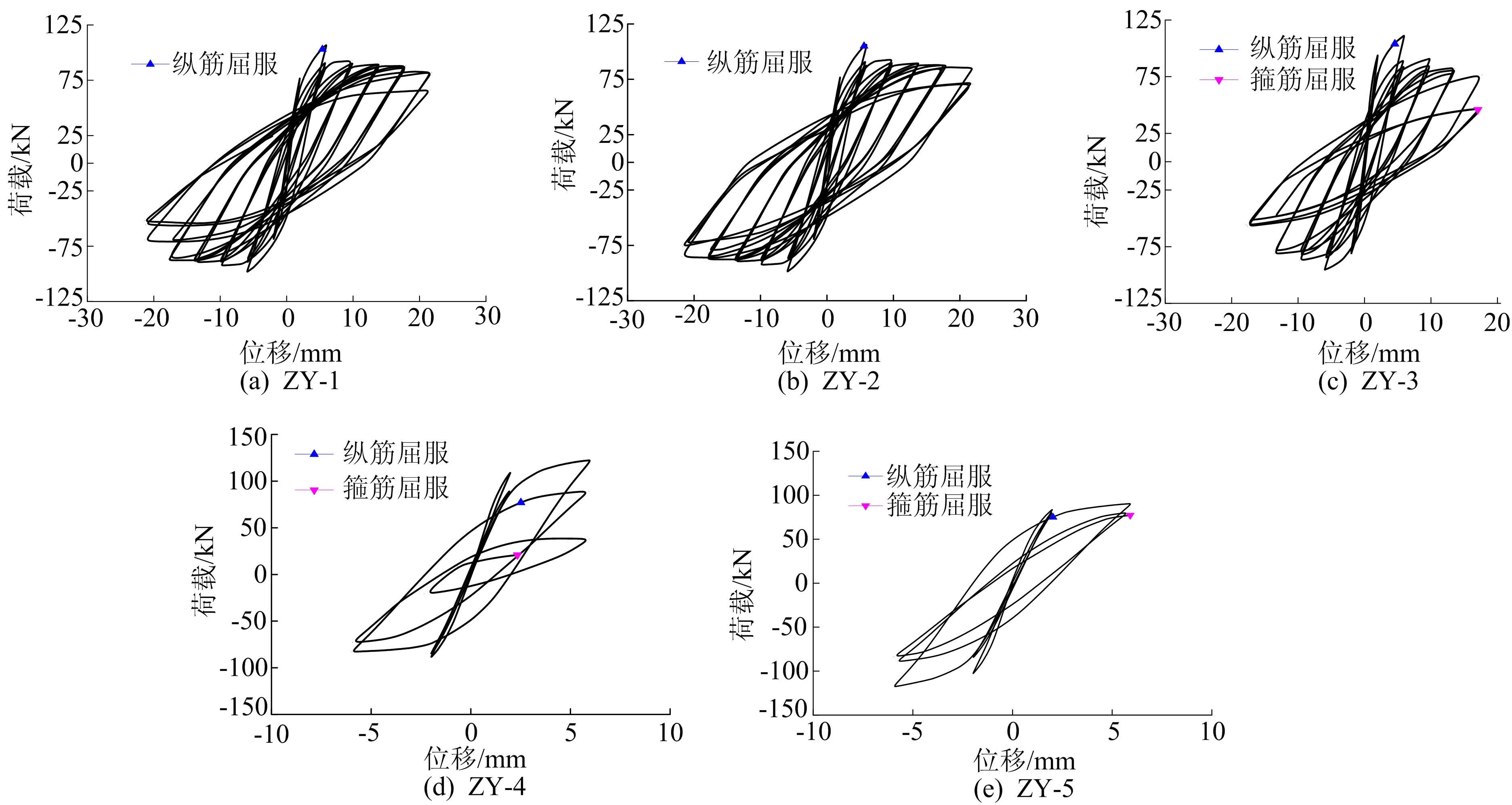
图9 轴压比组试件滞回曲线

构件荷载位移骨架曲线如图10所示,由图10可知，随轴压比增大构件屈服位移变化不大,但极限位移减小趋势明显,柱的延性显著降低。

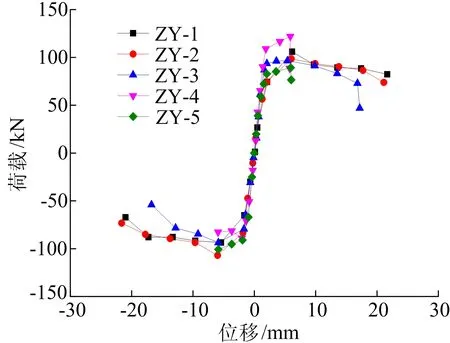
图10 轴压比组试件骨架曲线

3.2 混凝土强度

由表1可知,小于C50的柱发生弯曲破坏,大于等于C50的柱发生弯剪破坏。弯曲破坏柱随着混凝土强度增大,屈服荷载和屈服位移变化不明显,峰值荷载略增加,极限位移和延性略有减小;弯剪破坏柱随着混凝土强度增加,极限位移和延性明显下降。混凝土强度组骨架曲线如图11所示,由图11可知，随着混凝土强度增加,柱破坏模式发生转变时,柱的荷载和位移值均发生明显变化,弯曲破坏柱的承载力虽小于弯剪破坏柱,但变形能力明显较好。

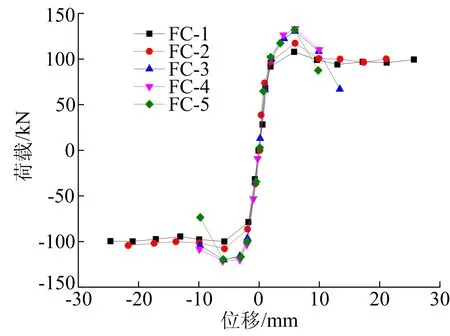
图11 混凝土强度组试件骨架曲线

3.3 配箍率

由表1可知,当柱配箍率大于0.3%时,柱由弯剪破坏转变为弯曲破坏,随着配箍率增加,柱屈服荷载和峰值荷载变化不大,但箍筋增加后造成约束混凝土效果增强,柱极限位移明显增加。箍筋组骨架曲线如图12所示,从图12可以看出，发生弯剪破坏柱的骨架曲线明显会出现下降段,构件耗能能力下降。

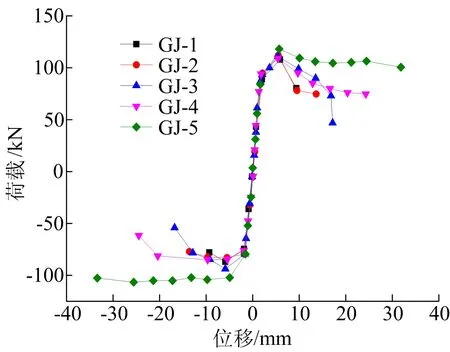
图12 箍筋组试件骨架曲线

4 破坏模式判别

目前,对于钢筋混凝土柱破坏模式的判别方法有很多种,从破坏机理层面对柱地震破坏模式的方法仅适用于试验或模拟研究。为适应工程需要,许多学者提出了不同的柱地震破坏模式判别方法。文献[2]通过建立与柱轴压比n、剪跨比λ、配筋率ρl、配箍率ρsv、钢筋和混凝土强度fc等参数相关的概率指标，其计算公式为:

(2)

通过计算概率指标得出相应构件破坏模式,当ω≤0.13时,柱发生弯曲破坏；当0.13<ω≤0.20时,柱发生弯剪破坏。文献[13]采用位移延性系数μ区分柱地震破坏模式,μ<1为剪切破坏,1<μ<4为弯剪破坏,μ>4为弯曲破坏。文献[14]给出了以构件弯剪比,即构件抗剪需求VM与抗剪承载力Vu的比值,为界限的破坏模式判别方法,当柱剪跨比λ>2时,0.6≤VM/Vu<1发生弯剪破坏;VM/Vu<0.6发生弯曲破坏。

本文采用上述文献中的3种方法对3组15个模拟柱数据进行破坏模式判别,结果见表2所列。文献[2]基于概率统计值的判别结果离散性较大,判别中多个试件与模拟输出的破坏机理不符,如轴压比组的ZY-3试件,混凝土强度组的FC-1和FC-2试件,箍筋组的GJ-1和GJ-3试件。文献[13]提出的位移判别法只将轴压比组的ZY-1和ZY-2试件判别为弯剪破坏,其他试件结果与破坏机理结果一致，但该方法基于柱延性系数,需要准确计算柱的侧向变形值。文献[14]基于柱承载力得出柱地震破坏模式,判别结果中仍有3个构件与机理结果不符。但相对于前2种方法构件承载力计算容易实现,适用范围更广。另外文献[14]中以弯剪比0.6来作为区分弯曲和弯剪破坏的界限较为保守,由表2可知,如以弯剪比0.65为界限时,所有试件的破坏模式判别结果与机理结果一致。表2中，VM=M/(λh)，h0为截面有效高度,M和Vu的值采用文献[6]中受弯承载力和受剪承载力公式计算得到。

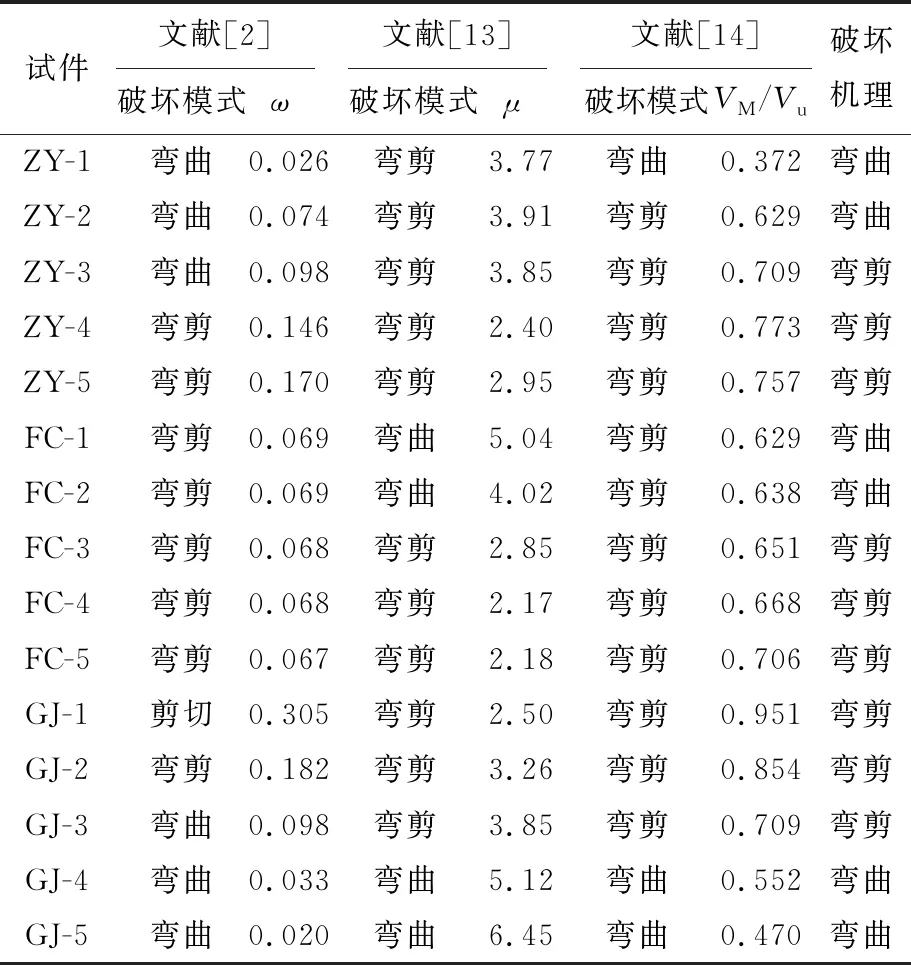
表2 3种方法判别柱地震破坏模式结果

5 结 论

(1) 本文采用混凝土塑性损伤模型和单轴滞回钢筋本构建立的有限元模型可以很好地模拟钢筋混凝土柱拟静力试验过程,从破坏形态、滞回曲线和破坏机理3个区分往复荷载作用下钢筋混凝土柱的地震破坏模式。

(2) 采用材料破坏机理来准确定义柱的不同破坏模式,随轴压比、混凝土强度和配箍率参数变化,柱破坏模式均有转变。随轴压比增大,构件推覆承载力先上升后下降,延性显著降低;混凝土强度增加时,构件承载力上升但延性下降;配箍率增加对构件承载力影响不大,但构件延性显著提高。

(3) 本文在已有方法的基础上，结合模拟结果给出柱弯曲和弯剪地震破坏模式的界限。在剪跨比λ>2的柱中,VM/Vu<0.65时柱发生弯曲破坏,0.65≤VM/Vu<1时,柱发生弯剪破坏。