面板数据均值共同变点分析在高校在校成绩上的应用

谭常春, 李曼丽

(1.合肥工业大学 经济学院,安徽 合肥 230601; 2.合肥工业大学 数学学院,安徽 合肥 230601)

国外关于高校学生成绩有一些研究。文献[4]使用meta分析方法研究得到拖延症与高校成绩之间存在负相关关系;文献[5]认为大麻的使用对高校学生成绩有消极影响;文献[6]采用路径分析验证了种族认同对高校学生成绩有正向影响;文献[7]认为心理韧性与高校学生成绩呈现显著正相关关系;文献[8]通过移动社交媒体的使用对高校学生成绩产生消极影响;文献[9]研究了电子设备的使用时间与成绩之间存在负相关关系;文献[10]采用meta路径分析认为人的五大性格特点及自我效能均会对高校学生成绩产生直接或间接的影响;文献[11]采用meta分析面板滞后模型的方法研究自我效能与成绩表现之间的关系,结果表明两者互为因果,相互促进。

关于面板数据均值共同变点的研究有很多。文献[12]使用最小二乘估计面板数据的均值变点,并给出变点估计量的一致估计和渐近分布；文献[13]基于累积和(cumulative sum,CUSUM)方法检测面板数据均值变点，并讨论了面板的相依关系对变点检测的影响；文献[14]采用拟似然方法检测面板数据的均值变点；文献[15]用CUSUM类型的比率统计量和Bootstrap统计量检测固定小样本面板数据中的均值变点；文献[16]提出CUSUM估计量来估计面板数据的均值变点,并与文献[12]提出的普通最小二乘法(ordinary least square,OLS)进行对比,结果显示CUSUM方法更佳;文献[17]基于CUSUM思想研究面板数据的均值变点,并给出估计量的一致估计和渐近分布;文献[18]在文献[12]基础上研究带有截面共同因子的面板数据均值变点,并将该方法应用于23种货币对美元的交换率以及113个国家的人均GDP数据。

本文将均值共同变点检测和估计理论应用于高校在校成绩分析中,主要是基于CUSUM比率统计量[15]进行模拟，并将该方法应用于合肥工业大学数学学院学生的成绩数据来判断学生成绩是否存在显著性结构变点,分析存在变点的原因,从而为提高学生成绩、优化高校课程安排、促进教学改革等提供参考。

1 面板数据均值共同变点检验

设Yi,t表示个体i(i=1,2,…,N)在不同时期t(t=1,2,…,T)的观测值。带有均值共同变点的面板数据模型为:

Yi,t=μi+δiI{t>τ}+σεi,t,

1≤i≤N, 1≤t≤T

(1)

其中，μi为数据的面板均值；δi为变点前后均值的差；σ为方差刻度参数,且σ>0；τ为真实变点,τ∈{2,…,T}；εi,t为随机扰动项；T固定;N→∞。

假设面板数据至少存在一个均值共同变点,则检验面板数据是否存在均值变点等价于检验假设:

H0:δi=0,i=1,2,…,N。

应用面板均值共同变点检验统计量[15]:

(2)

“数学教育中的历史与认识论欧洲暑期大学”这个名字起源于法国，自1975年法国数学教育学会成立以来，他们就把历史和认识论联系在一起，并用于会议名称、书籍名称等．“数学教育中的历史与认识论欧洲暑期大学”中的“认识论”含义为何呢？该词约于19和20世纪之交引入，至少包含以下4层含义．

引理1 当H0成立,[εi,1,…,εi,T]T,i=1,…,N为i.i.d.,对任何给定i,εi,t满足条件滞后期s独立且E(εi,t)=0,Var(εi,t)=1。记

ρt=Corr(εi,s,εi,s+t), ∀s∈{1,…,T-t},

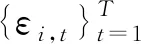
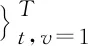
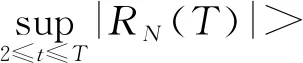
(3)

2 临界值ΓαMonte Carlo模拟计算

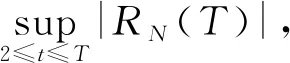
进行Monte Carlo模拟时,考虑到实际数据,本文取σ=1,δi=0,N=806,T=8,误差项εi,t服从AR(1)模型,其中a=-0.3、-0.2、0.2、0.3。模拟结果见表1所列。

表1 α=0.05的检验统计量临界值

3 高校在校成绩分析

选取合肥工业大学数学学院2008—2012级数学与应用数学和信息与计算科学2个专业学生的专业必修课成绩及加权平均成绩数据为样本,删除退学、休学、延迟毕业、编下以及代培生等其他情况的学生成绩之后,共有806×8个成绩数据,故N=806,T=8。其中加权平均成绩，即平均学分绩点(grade point average,GPA)计算公式如下:

3.1 GPA数据相关分析

本文旨在研究数学学院学生的8个学期成绩是否在某一学期发生显著变化。用Stata14对GPA数据在时间维度上进行自相关性检验,检验结果如下F(1,805)=4.905，P=0.027，给定显著性水平0.05,应拒绝原假设,说明数据在时间维度上存在一阶自相关。

使用Stata14对去均值GPA数据在时间维度上进行自相关性检验,检验结果表明在给定显著性水平为0.05情况下,去均值GPA数据在时间维度上存在一阶自相关关系,说明数据满足面板数据均值共同变点模型所需的条件。

3.2 GPA数据变点分析

Monte Carlo模拟得到的检验统计量临界值见表1所列,实证分析所得检验统计量见表2所列。对比表1、表2可以发现,在显著性水平0.05下,实证分析所得检验统计量均小于模拟得到的检验统计量临界值,说明高校成绩不存在变点,也即学生成绩的平均水平在8个学期内无显著变化。换言之,数学学院所有学生大学4 a的考试成绩总体上并未出现大幅波动,成绩好的同学会基本保持好成绩,而成绩一般或较差的同学其成绩也没有大幅提高或降低。成绩数据不存在变点可能存在以下几点原因:① 数学学院所有学生的考试成绩在8个学期确实不存在显著变化,此方法在检验微小变化时不够灵敏;②T=8太小;③ 模型的假设条件不符合真实数据的特点。

表2 GPA实证分析检验统计量

考虑到将数学学院2008—2012级所有学生成绩汇总分析可能会覆盖专业与专业之间的差异性及变化趋势,导致变点受到总体变化趋势的冲击而消失。因此将所收集的数学学院学生成绩按照专业进一步分类分析。

4 分专业高校成绩分析

按照专业分类,可以分为数学与应用数学专业和信息与计算科学专业。由于2个专业人数相近,为方便分析,取N=400,T=8。通过自相关检验及相关系数的计算,本文对重新分类的数据进行模拟和实证分析,见表3所列。

表3 2个专业GPA实证分析检验统计量RN(T)

数学专业和信息与计算科学专业学生GPA数据的分析结果见表3所列。分专业Monte Carlo模拟临界值的结果见表1所列。对比表1和表3可知，数学与应用数学专业学生成绩在α=0.05时不存在变点,说明数学专业的成绩在8个学期内无显著变化。由表1、表3可知信息与计算科学专业学生成绩在α=0.05情况下,在第5学期和第7学期存在显著变点,说明信息专业学生成绩在第5学期和第7学期成绩变化较为显著。数学与应用数学专业不存在变点可能与专业性质有关,数学与应用数学专业由于课程设置及课程难度相比于其他专业更为高深,且学生的学习和接受能力比较稳定,因此考试成绩也较为稳定。而信息与计算科学专业在第5学期(大三上学期)和第7学期(大四上学期)分别存在一个变点，可能是因为专业性质与数学与应用数学专业不同,大三学年是决定本科毕业发展的关键一年,学生更加努力学习提高成绩,所以成绩变化较为明显,易产生变点;而在大四学年,学生已根据学校发布的读研、出国及就业等相关政策确定未来发展方向,花费更多时间在工作实习、出国深造或准备保研考研笔试面试等方面,对成绩重视程度大不如前,导致成绩出现显著下降的趋势,故产生变点。

5 结 论

本文基于面板数据均值共同变点理论，检验高校成绩是否在8个学期内发生显著性结构变化。得到结论如下:

(1) 数学学院所有学生成绩在8个学期均未出现变点,说明数学学院学生大学4 a的考试成绩总体上并未出现大幅变化。

(2) 将数学与应用数学专业和信息与计算科学专业单独分析,发现信息与计算科学专业的学生在显著性水平为0.05的情况下存在2个显著变点,而数学与应用数学专业不存在变点。说明专业之间的成绩变化具有差异性,且整体变化性趋势会对局部趋势产生覆盖影响。出现以上结果可能的原因是数学与应用数学专业的专业特殊性及学生学习、接受能力的稳定性使得考试成绩不会有较大变动,而信息与计算科学专业学生成绩在第5学期和第7学期发生显著的变化与课程安排、学生特定时期的心理活动以及与当年学校发布的政策紧密相关。