基于五点三次平滑和ARMA的次同步振荡参数辨识
王雨虹, 杨明昆, 包伟川, 付 华, 徐耀松
(1.辽宁工程技术大学 电气与控制工程学院,辽宁 葫芦岛 125105; 2.辽宁工程技术大学 安全科学与工程学院,辽宁 阜新 123000; 3.国网阜新供电公司,辽宁 阜新 123000)
0 引 言
电力系统次同步振荡是由于电力系统和汽轮发电机轴系的相互激发、相互助增引起的一种振荡失稳行为,振荡频率为2.5~50 Hz。频繁的次同步振荡会造成发电机轴系严重受损,导致电网不能正常运行[1]。因此,准确、快速、有效地辨识次同步振荡模态,对进一步分析和抑制次同步振荡至关重要[2]。
随着广域测量系统(wide area measurement system, WAMS)的普遍使用,模态参数在线辨识已经成为研究电力系统次同步振荡问题的主要手段。目前,典型的辨识方法有Prony法、快速傅里叶变换 (fast Fourier transform,FFT)、小波分析法、希尔伯特-黄变换(Hilbert-Huang transform,HHT)算法和矩阵束法等。Prony算法对仿真结果和实时测量数据均可有效分析,但在识别含噪次同步振荡信号时误差较大[3-4];FFT可以缩短模态辨识时间,提高辨识效率,但无法提取振荡的瞬时频率和衰减因子[5];小波分析法能够改变信号时间窗和频率窗,实现时频局域化分析,但较难辨别相近的频率成分,不能准确提取模态阻尼系数[6];HHT算法在研究非线性非平稳信号时具备完全自适应性,时间和频率能够同时得到高精度,但会呈现端点效应和模态混叠状态,对辨识效果影响较大[7];矩阵束方法实质是一种线性化的近似研究措施,不适用于电力系统较大扰动(非线性强)时的振荡数据[8-10]。
综合以上研究成果,本文将五点三次平滑算法和自回归滑动平均(auto-regressive moving average,ARMA)算法相结合使用。五点三次平滑法的原理是利用最小二乘法构造三次最小二乘多项式,对含有噪声的采样数据进行平滑去噪[11],算法简单,去噪性能强。ARMA模型时序分析法是一种运用参数模型对有序随机振荡响应数据进行处理,是应用最广泛的模态参数识别方法。对电力系统次同步振荡进行模态辨识时,将去噪后的信号看作一组有序随机振荡响应数据,再建立ARMA模型进行模态参数辨识,可达到较高的辨识精度。2种算法结合达到了去噪性能好和辨识精度高的目的,弥补了上述传统辨识方法在次同步振荡模态参数辨识中的缺陷。
1 基于五点三次平滑去噪
电力系统中的电力电子设备和谐波污染,会造成从现场采集的信号数据中含有大量的噪声干扰。电力系统在受到噪声干扰时,混合信号可表示为次同步振荡衰减信号与随机噪声干扰信号的叠加。混合信号模型为:
y(t)=x(t)+ν(t)
(1)
(2)
其中,y(t)为混合信号;x(t)为次同步振荡衰减信号;ν(t)为噪声干扰信号;Ai为振荡幅值;σi为衰减系数;fi为频率;φi为初相。
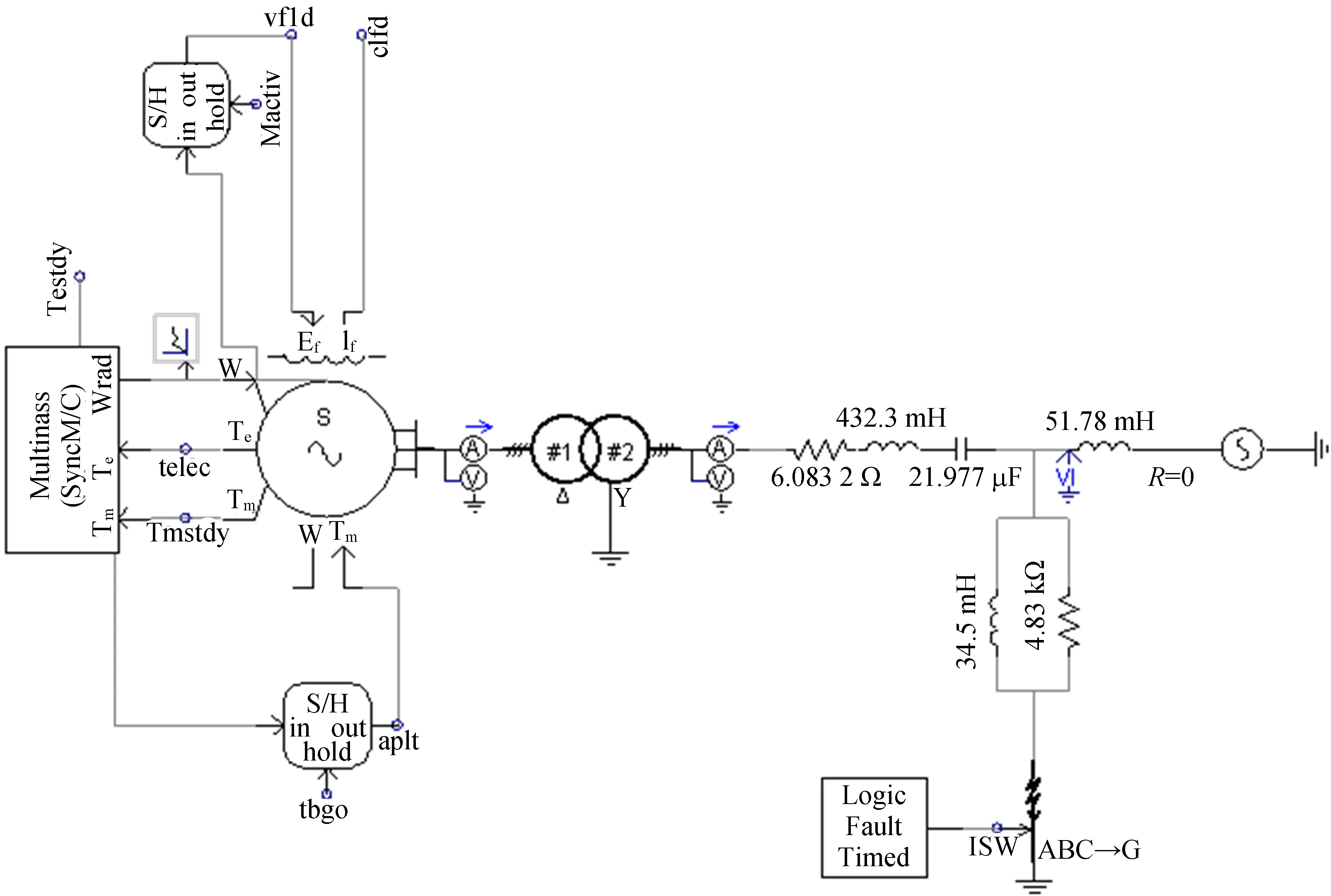
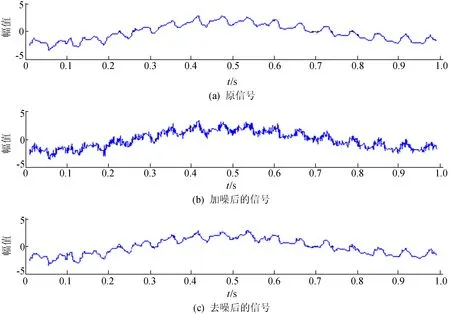
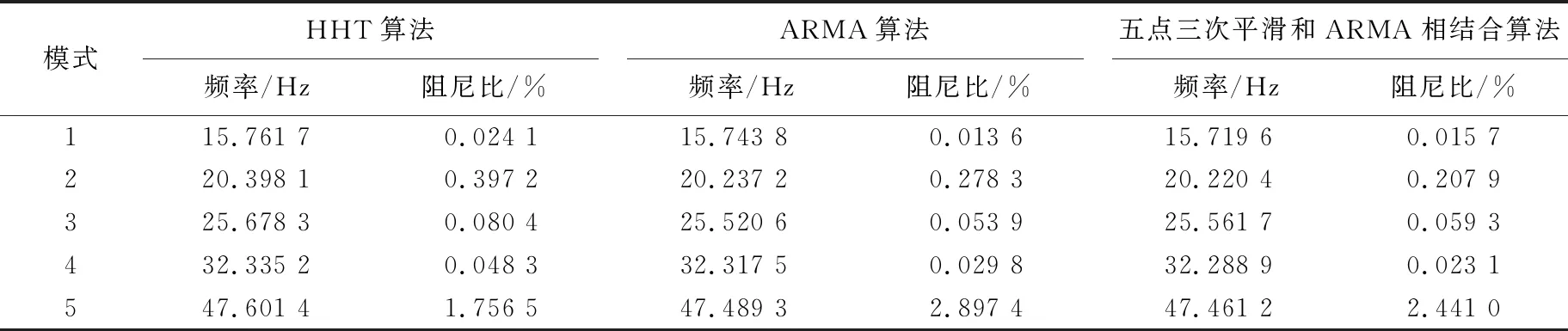
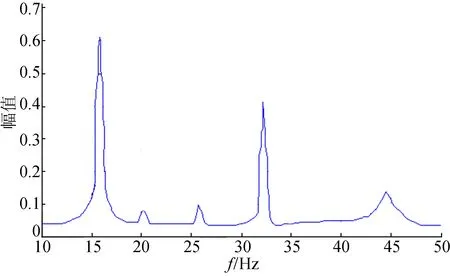
设在n+1个等间距采样点X0 Y(μ)=a0+a1μ+a2μ2+…+am-1μm-1+amμm (3) 用最小二乘法来确定多项式中的待定系数aj,令方差和为: (4) 要使方差和F(a0,a1,a2,…,am)为最小,可对aj(j=0,1,2,…,m)求偏导数,必有: (5) 整理后可得正规方程组: (6) 将n=4,m=3代入(6)式可解出aj(j=0,1,2,3),将aj(j=0,1,2,3)代入(3)式,令μ=0,1,2,3,4,可得到五点三次平滑公式,即 (7) (8) (9) (10) (11) 由(7)~(11)式可知,对于等间距采样点,只用到采样数据Yi,与节点Xi及节点间距大小h无关[12]。 采样得到的数据远大于5个,除首尾4个端点外,其余各点都能找到前后2个相邻点,为了对称起见,首尾4个端点分别用(7)式、(8)式、(10)式、(11)式进行修正,其他端点都用(9)式进行平滑。 在电力系统次同步振荡现象中,文献[13]对次同步振荡小扰动响应信号和高斯白噪声信号进行谱分析研究,结果表明,两者能量分布都集中在某一频段内,其他频段能量基本可忽略。因此,可将其中的小扰动看作高斯白噪声,利用ARMA模型的随机差分方程形式描述系统响应。 将去噪处理后的次同步振荡信号看作零均值、平稳时序{xt}(t=0,1,2,…),建立ARMA模型为: (12) 其中,xt为时序{xt}在t时刻的元素;αk(k=1,2,…,N)、βq(q=1,2,…,M)分别为自回归(autoregressive model,AR)部分和滑动平均(moving average,MA)部分模型参数;N、M分别为AR部分和MA部分模型阶次;gt为随机小扰动时序{gt}在t时刻的元素,在研究系统次同步振荡时,时序{gt}应为高斯白噪声。 模型阶数的高低决定振荡模态提取结果的准确性。若模型阶数过高,则模型将包含过多的不相关振荡成分;若模型阶数过低,则容易忽略掉部分振荡模态信息。因此选择合适的模型阶数是利用ARMA模型进行模态参数估计的关键步骤[14-15]。 本文采用BIC准则进行ARMA模型定阶,定义如下: (13) BIC准则公式有2项相加构成:前者随模型阶数的升高而变小,可衡量模型拟合的好坏程度;后者通过改变模型阶数p,来得出p对模型精度的影响权重大小。与其他模型定阶措施相比,BIC准则定阶可增加模型阶数的作用,判别出的适用模型阶次更低,而且BIC准则确定的模型阶数是其真值的一致估计。 设相关函数R的长度为H,由(12)式知MA部分模型阶数为M,可得如下矩阵方程: (14) 其中,RJ(J=M+1,M+2,…,H)为时序{xt}的J步自协方差函数[16],计算公式为: (15) 通过求解方程(14)可求得AR部分模型参数α1,α2,…,αN。 估计出ARMA模型的参数后,可得对应的特征方程为: 1-α1z-1-α2z-2-…-αNz-N=0 (16) 其中,z为系统特征方程的特征根。 (17) 其中,Δt为采样时间间隔;fi为次同步振荡频率;ξi为次同步振荡阻尼比。 基于五点三次平滑去噪和ARMA算法的次同步振荡模态辨识步骤如图1所示,具体步骤如下: (1) 提取WAMS中的PMU次同步振荡实测信号数据,对采样信号进行基于五点三次平滑去噪处理。 (2) 对去噪后的信号建立ARMA模型,考虑到去噪处理后的实测数据(如信号幅值严重超限、信号传输失败等造成的数据污染)会影响到在线振荡参数辨识的准确度。因此,需要对数据进行预处理,包括检测异常数据、去趋和零化处理以及标准化处理。 (3) 根据BIC准则对ARMA模型进行模型定阶,电力系统在实际运行过程中,可能会时常发生各种大小故障,导致系统结构发生变化,从而使初始阶数不再适用,需要对模型进行重新定阶。 (4) 按照(14)式、(15)式进行模型参数估计,并通过(17)式计算并保存次同步振荡模态参数。 图1 次同步振荡模态辨识流程 构造理想测试信号表达式,即 x(t)=x1(t)+x2(t)+x3(t), (18) 为验证五点三次平滑算法在强噪声环境下的去噪效果,在信号中增加均值为0、方差为0.8的高斯白噪声,并对加噪后信号进行平滑去噪,原信号和噪声去除前后的信号如图2所示。 由图2可知,五点三次平滑算法具有非常好的去噪效果。 图2 原信号和去噪前后的信号 由上述理想信号模型可知,该信号包含3个振荡模式,频率分别为15.7、20.2、32.2 Hz,阻尼比分别为0.131 8%、0.197 0%、0.296 6%。分别采用五点三次平滑和ARMA相结合算法、ARMA算法和HHT算法对加噪后的信号进行辨识,频率和阻尼比的辨识结果见表1所列。 从表1可以看出,五点三次平滑和ARMA算法相结合方法对频率和阻尼比的辨识误差分别小于0.02%和3.10%,和其他2种算法相比,辨识精度最高。 表1 3种方法辨识结果对比 为了进一步验证本文方法的有效性,采用PSCAD软件搭建IEEE第一标准模型系统。该系统图主要包括发电机模型、变压器模型、输电线路模型、串补电容器、无穷大电源等部分。系统建模简化图如图3所示。 图3 IEEE第一标准模型系统建模简化图 本算例采用的分析对象是发电机转速偏差信号[17-18]。为得到转速偏差信号,在1.5 s时,系统在串补电容与无穷大电源之间经过渡阻抗发生三相短路接地,故障持续时间为75 ms,录取1~2 s时段的转速偏差信号波形。 线路参数设置为:线路电阻RL=6.083 2 Ω、线路电抗XL=432.3 mH、串补电容XC=21.977 μF、无穷大系统等值电抗XS=51.78 mH。该模型发电机轴系存在5个扭振频率,依次为15.71、20.21、25.55、32.28、47.45 Hz。 为验证五点三次平滑算法的去噪性能,在原始信号上加入SNR=10的高斯白噪声。采用HHT算法、ARMA算法和五点三次平滑与ARMA相结合算法分别对含噪声的发电机转速偏差信号进行模态辨识,去噪结果对比如图4所示,辨识结果对比见表2所列。 图4 转速偏差原始信号和去噪前后信号 表2 3种算法对含噪声发电机转速偏差信号辨识结果对比 模式HHT算法频率/Hz阻尼比/%ARMA算法频率/Hz阻尼比/%五点三次平滑和ARMA相结合算法频率/Hz阻尼比/%115.761 70.024 115.743 80.013 615.719 60.015 7220.398 10.397 220.237 20.278 320.220 40.207 9325.678 30.080 425.520 60.053 925.561 70.059 3432.335 20.048 332.317 50.029 832.288 90.023 1547.601 41.756 547.489 32.897 447.461 22.441 0 由图4、表2可知,在发电机转速偏差信号中加入强噪声后,五点三次与ARMA算法相结合方法最接近于频率和阻尼比的理论值,从而说明本文方法在实际应用系统中也具有良好的辨识效果。对发电机转速偏差信号进行FFT变换,结果如图5所示。 图5 发电机转速偏差信号FFT变换结果 由图5可知,模态15.71 Hz和32.28 Hz的幅值较大,表2中2种模态阻尼比较小。由阻尼比越小,振荡衰减速度越慢可知,图5、表2表现为一致性,从而可断定模态15.71 Hz和32.28 Hz为该系统主导振荡模式。由表2可知,模态47.45 Hz的阻尼比较大,表明此模态振荡衰减速度较快,与图5中时域仿真结果相符。从而进一步验证了本文所提方法的正确性和实用性。 (1) 本文将五点三次平滑去噪与ARMA算法相结合,应用于次同步振荡模态参数辨识,可对原始振荡信号进行有效去噪和模态参数精确辨识,克服了传统辨识算法去噪性能和辨识精度低的缺点。 (2) 该方法不必考虑产生次同步振荡的机理类别和性质,可直接对WAMS量测数据进行模态识别。对系统运行在强噪声干扰时产生的信号数据,首先采用五点三次平滑算法进行去噪处理,然后对处理后的信号建立ARMA模型进行模态参数估计,完成次同步振荡精确辨识。 (3) 算例证明了所提算法在去噪能力和辨识精度的优越性,为次同步振荡在线分析和抑制措施研究提供了可靠的理论依据。
2 ARMA算法
2.1 ARMA模型建立
2.2 ARMA模型定阶

2.3 基于ARMA模型的模态参数估计

3 次同步振荡模态辨识算法流程
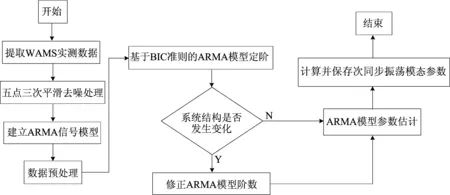
4 算例仿真分析
4.1 理想信号算例


4.2 IEEE第一标准模型仿真分析
5 结 论

