GPS/BDS组合多天线定姿与精度分析

杨鸿毅, 王潜心, 胡 超, 毛 亚, 柴大帅

(中国矿业大学 环境与测绘学院,江苏 徐州 221116)

0 引 言

姿态反映的是载体相对于当地水平坐标系的角位置,是运动载体的重要导航信息[1]。传统的三维姿态参数获取是通过惯性导航系统(inertial navigation system,INS)[2-3]，但是,INS成本比较高,并且其误差会随时间积累[4-5]。近年来,随着载波测量技术和模糊度固定技术的不断发展,基于全球卫星导航系统(global navigation satellite system,GNSS)的高精度定姿越来越受到青睐，目前GNSS多天线定姿研究大多基于全球定位系统(Global Positioning System,GPS)[6-8],对北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)定姿的研究成果较少[9]。随着BDS不断发展[10],将BDS数据加入GNSS定姿中是一个必然的趋势。在原有GPS基础上加入BDS能更好地利用空中资源,并且能改善卫星的几何分布,从而削弱法方程系数矩阵的病态性,弥补单系统不足[11]。

利用基线向量解算载体姿态有2种算法——直接法和最小二乘法。直接法是通过代入基线向量坐标来解算姿态角;最小二乘法是将3个姿态角作为待估值,通过最小二乘迭代来解算姿态角[12-13]。直接法计算过程简单,计算速度快,但是不能同时利用多条基线估计姿态角,估值是次优的。最小二乘法理论上是最优的,但是需要较精确的初始值,迭代过程较为复杂。

本文以GNSS多天线定姿理论为基础,通过自编程序实现伪距和载波定姿、直接法和最小二乘法定姿,并在GPS定姿的基础上加上BDS数据,实现GPS/BDS组合定姿;实验利用2根天线进行静态数据采集,模拟载体静止状态。通过3组对比实验分别分析伪距与载波的定姿精度、直接法和最小二乘法的定姿精度、单GPS和GPS/BDS组合的定姿精度。

1 GPS/BDS组合定位观测方程

多天线定姿的第1步需要确定各天线的坐标,解算天线之间的基线,并确定相应的坐标框架,最后再进行定姿解算。主天线坐标通过单点定位解算得来,附属天线坐标通过差分定位获取。其中GNSS差分定位伪距和载波相位的观测方程分别为:

Δρ=ΔD-ΔVion+ΔVtro+Δε

(1)

λΔφ=ΔD-ΔVion+ΔVtro+

ΔN+Δε

(2)

(3)

2 多天线定姿方法

姿态求解的核心是载体坐标系与当地水平坐标系之间的旋转变换,当地水平坐标系旋转到与载体坐标系重合,需要引入3个欧拉角,并在欧拉角之间进行3次连续旋转变换,每次旋转变换都可以用一个旋转矩阵表示[15]。

其旋转模型为:

bi=R2R1R3li

(4)

(5)

E1=cosracosya-sinrasinpasinya,

E2=cosrasinya+sinrasinpacosya,

E3=-sinracospa,E4=-cospasinya,

E5=cospacosya,E6=sinpa,

E7=sinracosya+cosrasinpasinya,

E8=sinrasinya-cosrasinpacosya,

E9=cosracospa。

其中,ra为翻滚角(roll);ya为航向角(yaw);pa为俯仰角(pitch);bi为天线i在载体坐标框架下的坐标;li为天线i在当地水平坐标框架下的坐标。

2.1 直接法定姿

直接法是通过代数方法来求解载体姿态角,每次代入一条基线来求解载体的3个姿态角。载体坐标框架示意图如图1所示。

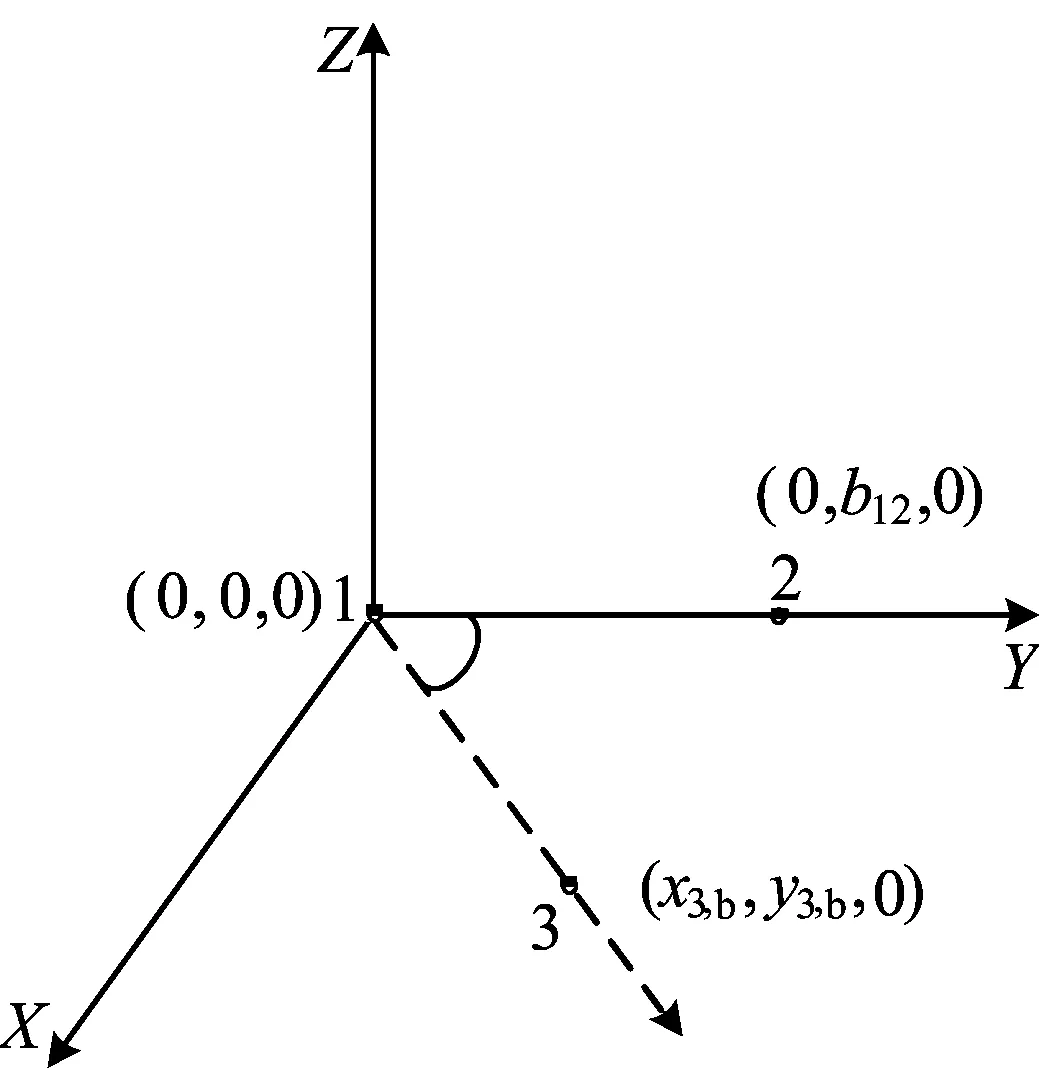
图1 载体坐标框架示意图

由图1可知,天线2和天线3在载体坐标系下的坐标分别表示为:

其中,b12为主天线到天线2的基线长。

由(4)式可得,天线2在当地水平坐标系下的坐标表示为:

(6)

由(6)式可知,ya和pa可以直接求得,即

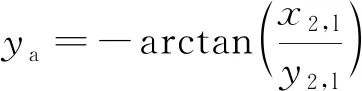
(7)

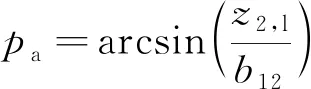
(8)

在求ra时,将天线3在当地水平坐标框架下的坐标先以ya和pa进行旋转,旋转变换公式为:

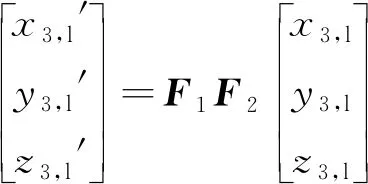
(9)

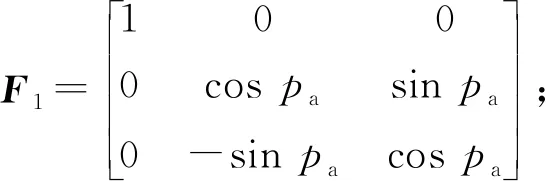
最后再将坐标旋转到载体坐标框架下的坐标,旋转变换公式为:

(10)

由(10)式可得,ra计算公式为:

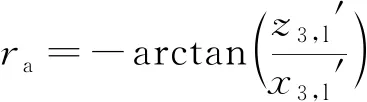
(11)

由(7)式、(8)式、(11)式可知,直接法不需要先验载体基线长度,直接利用观测值向量进行求解。

2.2 最小二乘姿态估计

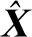
(12)

Li=bi-R2R1R3li,

其中,A为系数矩阵;P为相应矩阵所对应的权阵。

3 定姿结果精度分析

本次实验为获得稳定的姿态角,采用2台GPS/BDS双系统接收机同时进行静态数据采集,实验地点为中国矿业大学环境与测绘学院顶楼,采样频率为1 s。采集到的数据使用本文描述的方法自编程序分别处理。实验数据采集现场如图2所示。

图2 实验数据采集现场

3.1 伪距和载波定姿精度分析

GNSS多天线姿态测量有载波相位测量和码测量,载波相位测量的精度高于码测量。为了反映伪距测量和载波相位测量在定姿过程中的差异,本文使用伪距数据和载波相位数据分别进行多天线定姿。伪距和载波的基线解算结果如图3所示,见表1所列,伪距和载波姿态角解算结果如图4、图5所示,见表2所列。

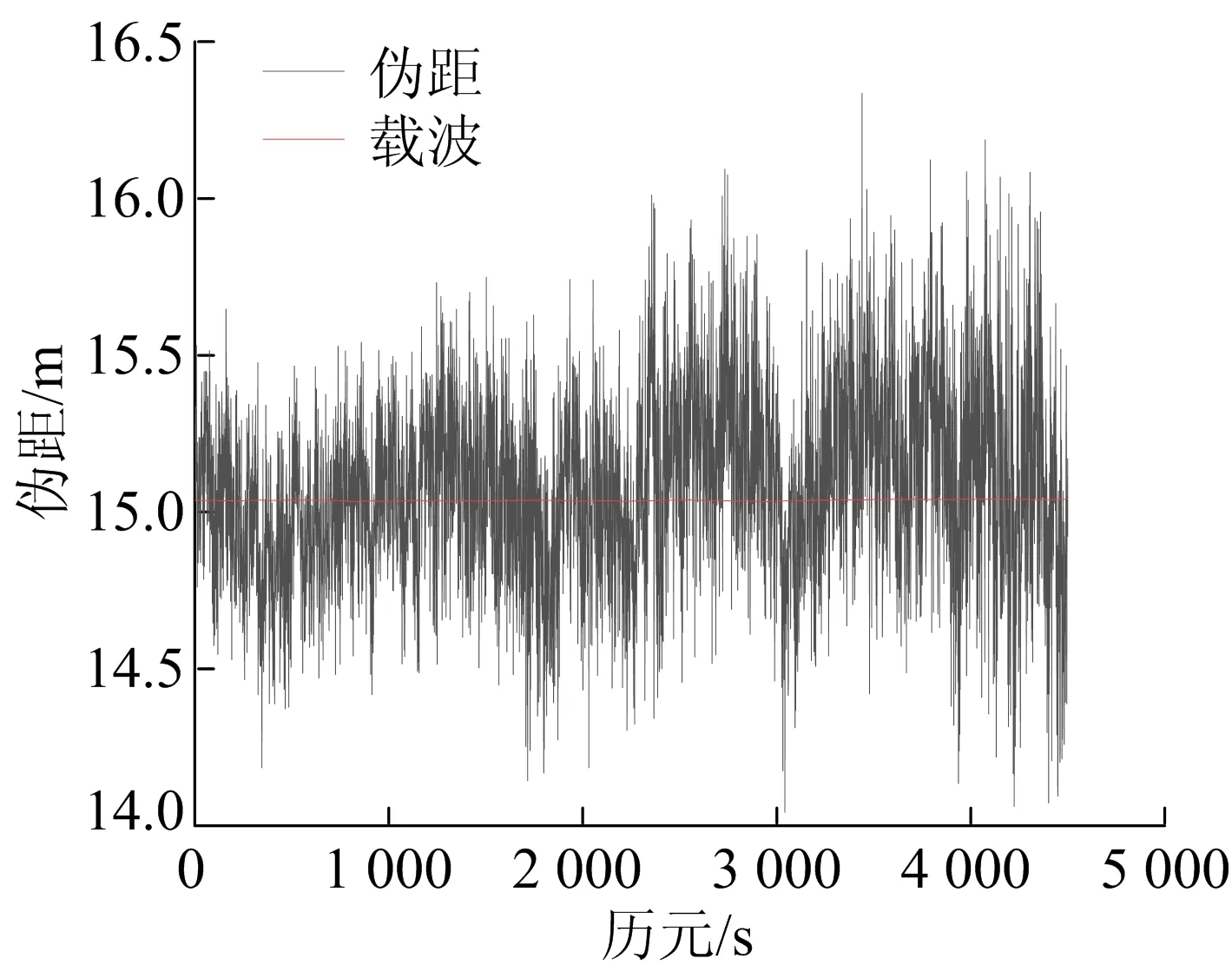
图3 伪距与载波基线解算结果

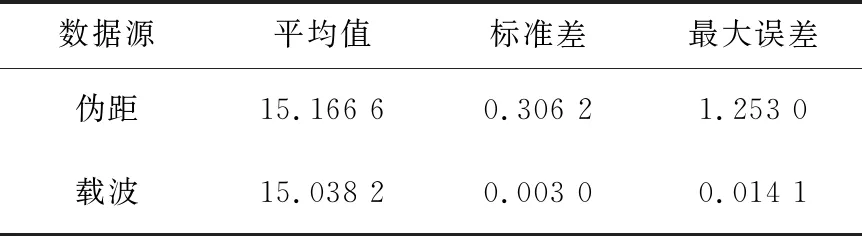
表1 伪距与载波基线解算统计分析结果 m

由图3可知,伪距解算的基线波动比较大,载波解算的基线比较平稳。由表1可知,从标准差看,载波明显小于伪距,表明载波解算基线稳定性较好;从最大误差看,载波最大误差小于伪距,说明载波控制误差的能力好于伪距。

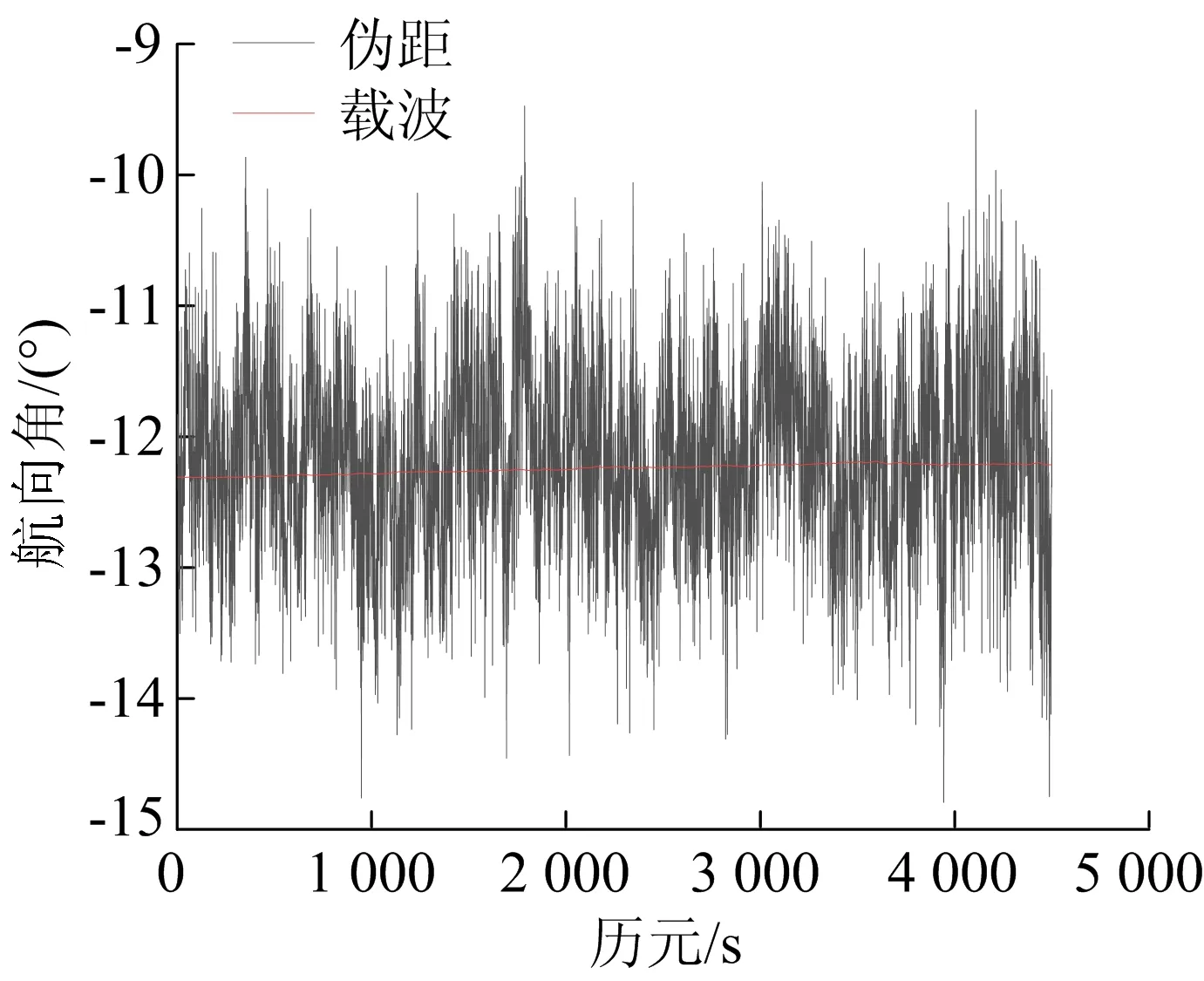
图4 伪距与载波航向角解算结果

图5 伪距与载波俯仰角解算结果

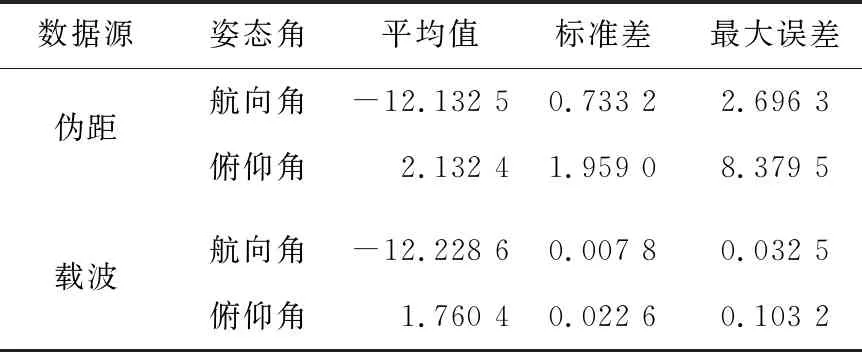
表2 伪距与载波姿态角解算分析结果 (°)

由图4、图5可知,使用伪距解算的姿态角变化幅度很大,使用载波解算的姿态角基本不变。由表2可知,从标准差看,载波解算姿态角的标准差远远小于伪距,说明载波解算姿态角的稳定性好于伪距;从最大误差看,载波解算姿态角的最大误差远远小于伪距,说明载波解算姿态角的控制误差能力优于伪距。

3.2 直接法和最小二乘法定姿精度分析

通过载波相位差分解算天线之间的基线后,分别进行最小二乘法和直接法定姿,2种算法解算姿态角如图6、图7所示,姿态角统计结果见表3所列。

由图6、图7可知,直接法和最小二乘法解算的姿态角基本一致。由表3可知,2种方法解算姿态角标准差和最大误差差别微小,说明2种算法解算姿态角的性能基本相当。

图6 直接法和最小二乘法航向角解算结果

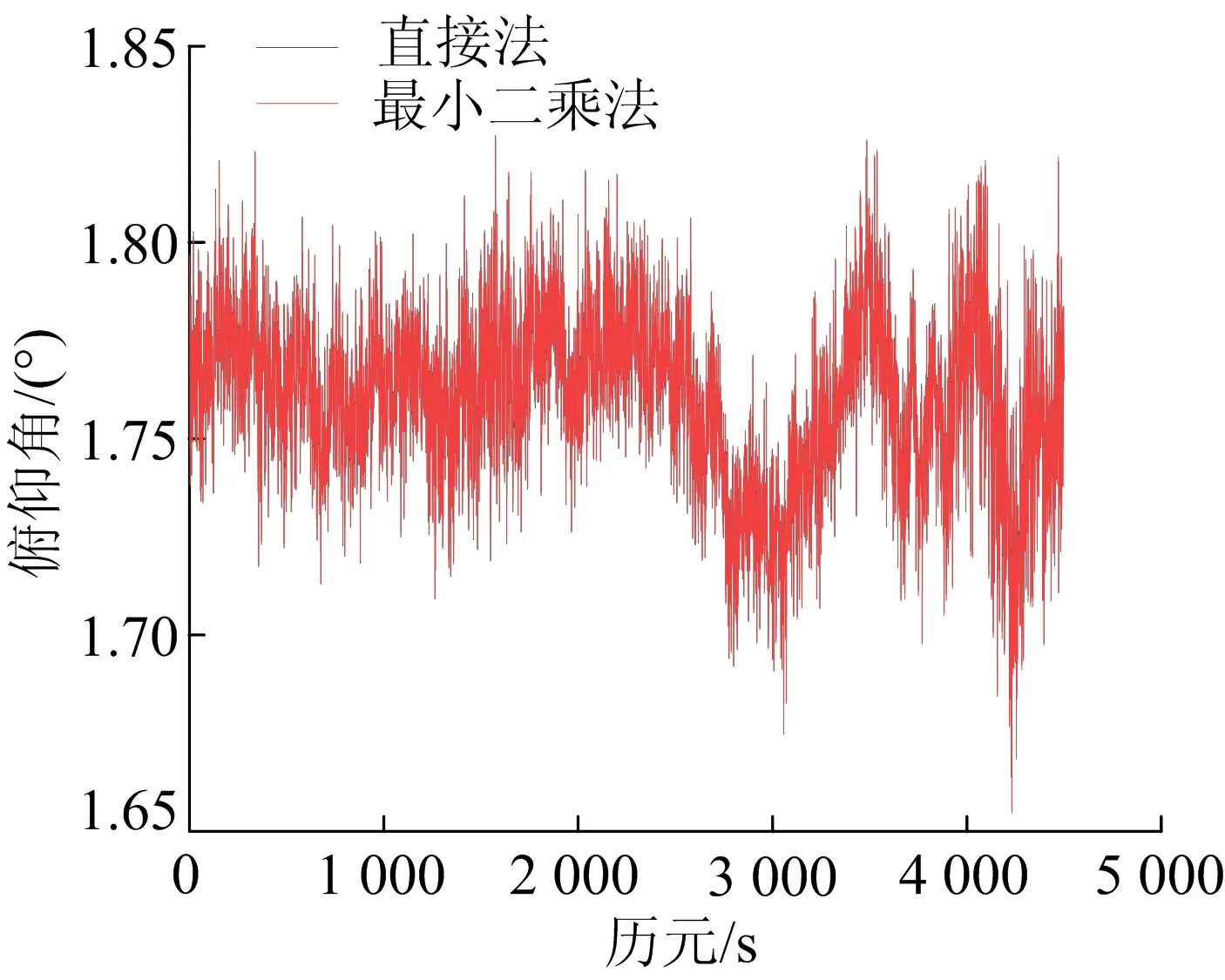
图7 直接法和最小二乘法俯仰角解算结果

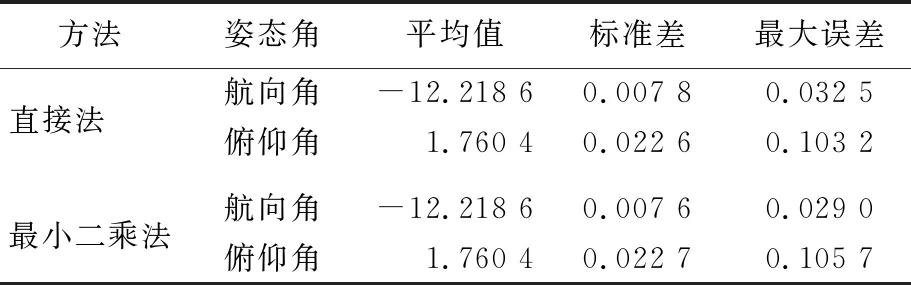
表3 2种方法姿态角解算结果统计分析 (°)

3.3 GPS与GPS/BDS组合定姿精度分析

在单GPS数据上加入北斗数据,形成GPS/BDS组合定姿。单GPS与GPS/BDS组合定姿可见卫星数目统计结果见表4所列。由表4可知,在整个数据处理阶段,GPS可视卫星数目只有6、7颗,而GPS/BDS双系统卫星的数目基本维持在19颗左右,可视卫星数目显著提高,从而反映了双系统组合定姿具有更高的可靠性。单GPS和GPS/BDS组合解算姿态角如图8、图9所示,姿态角结果统计见表5所列。

表4 可见卫星数目统计结果 颗

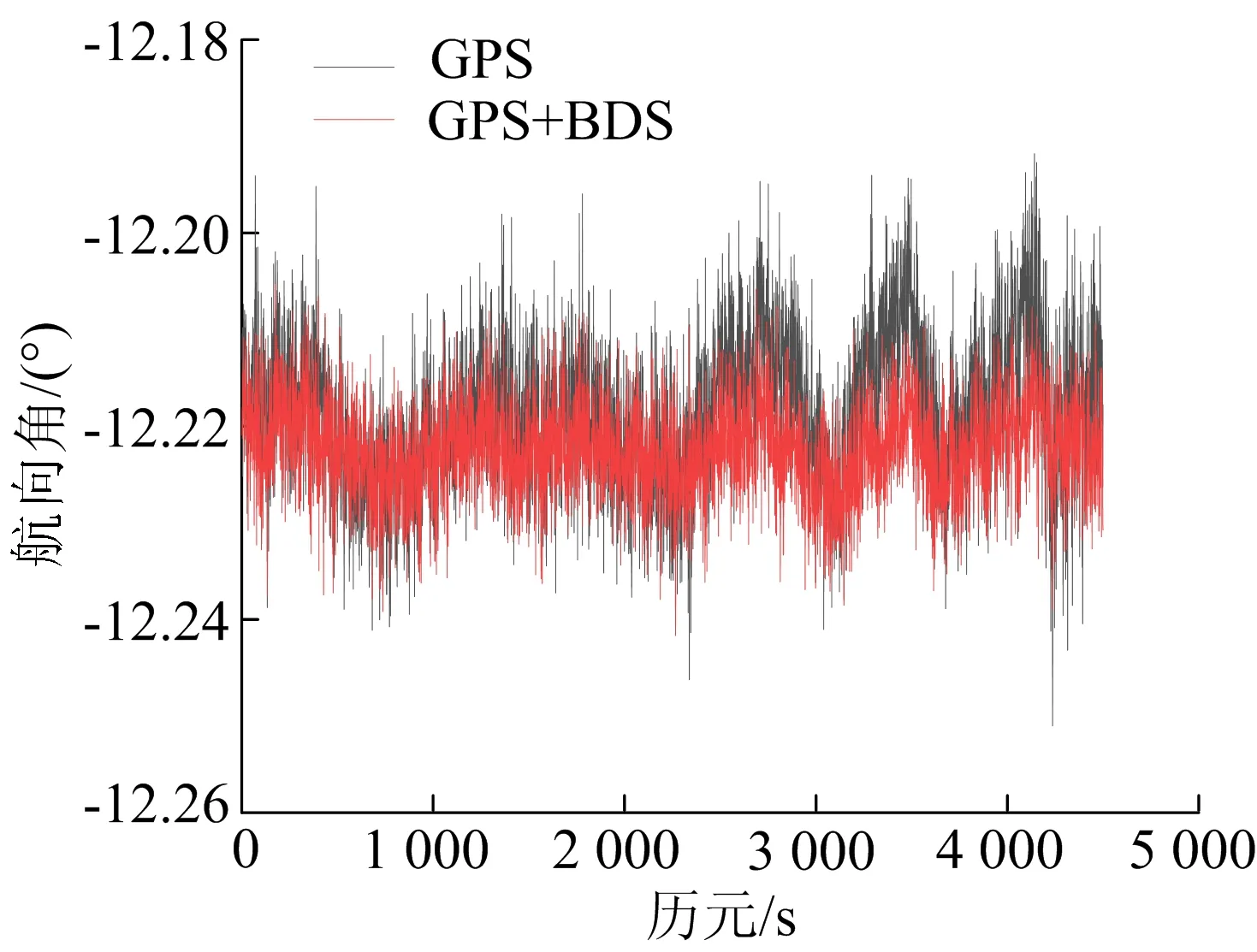
图8 2个系统航向角解算结果

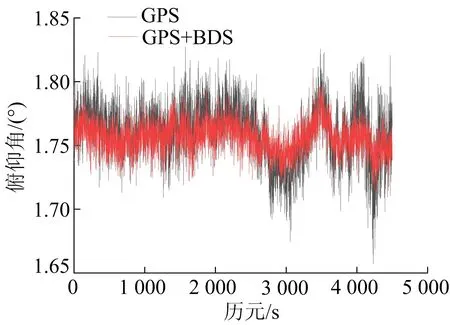
图9 2个系统俯仰角解算结果

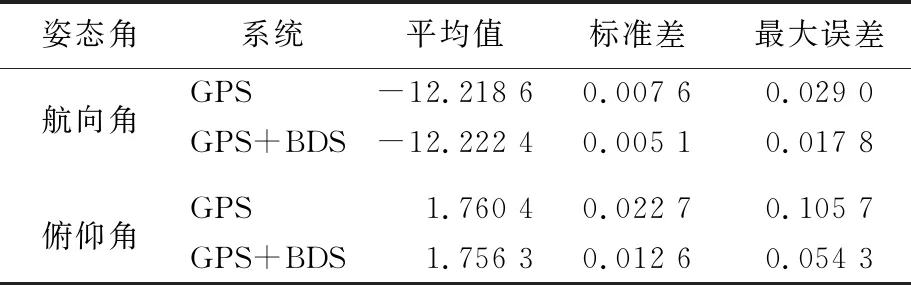
表5 2个系统姿态角解算结果统计分析 (°)

由表5可知,从标准差看,GPS/BDS组合解算姿态角的标准差比单GPS解算的要小,说明GPS/BDS组合解算姿态角稳定性优于单GPS;从最大误差看, GPS/BDS组合解算姿态角的最大误差小于单GPS,说明GPS/BDS组合解算姿态角的控制误差能力略优于单GPS。

4 结 论

本文对GNSS组合多天线定姿的数学模型进行了理论公式的推导,应用静态数据实施伪距与载波对比实验、直接法和最小二乘法定姿对比实验,在原有的单GPS数据上加入BDS数据,并实施单GPS和GPS/BDS组合定姿对比实验,得到如下结论:

(1) 伪距解算基线精度在m级,载波解算基线精度能达到mm级;使用载波解算姿态角精度大大优于伪距。

(2) 基于载波的直接法和最小二乘法解算静态载体的姿态角都具有较高的精度。2种方法解算载体姿态角的标准差和最大误差略微有所差别,定姿性能基本相当。

(3) GPS/BDS组合解算静态载体姿态角的标准差和最大误差小于单GPS,GPS/BDS组合定姿精度略优于单GPS。基于载波的GPS/BDS组合多天线定姿系统解算航向角和俯仰角的标准差分别为0.005 1°、0.012 6°,具备高精度定姿能力。