基于PSO-SVR近似模型的汽车正碰可靠性优化

高剑武, 李 旗, 李亚军, 谷先广

(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009; 2.合肥工业大学 智能制造技术研究院,安徽 合肥 230051)

0 引 言

随着中国经济的进步,中国汽车行业获得了突飞猛进的发展,同时也带来了能源消耗、环境污染、交通安全事故频发等问题。因此,对于汽车轻量化和安全性能的研究更加紧迫,汽车的多目标优化设计越来越重要。目前大多数优化只关注确定性优化设计(deterministic optimization design, DOD),未考虑不确定因素的影响[1-2],而加工误差等不确定因素是客观存在的,仅考虑确定性设计将直接影响产品的可靠性。为了满足生产和使用安全的要求,在优化设计过程中,可靠性优化设计(reliability optimization design, ROD)尤为重要。

高精度的近似模型是提高计算精度、缩短优化周期、寻找最优设计方案的基础。常用的近似模型有响应面模型(response surface model, RSM)、径向基函数(radial basis function, RBF)、Kriging(KRG)模型等。

然而响应面和人工神经网络等经典近似模型方法存在不可避免的缺点[3]。研究表明,支持向量回归(support vector regression, SVR)法可以较好地解决小样本、非线性、高维度、局部极小点等实际问题,具有很强的泛化能力[4],并且在结构可靠度分析领域得到广泛应用。近年来,许多学者在应用SVR近似模型方面进行了研究。文献[5]将SVR近似模型应用于潜水器的外形优化中,并通过比较SVR近似模型与传统近似模型的误差得出SVR模型更令人满意,但并未对SVR模型中的参数进行优化;文献[6]应用粒子群优化算法(particle swarm optimization, PSO)对SVR模型中的惩罚系数C进行优化,提高了SVR近似模型的精度,但并未对SVR模型中不敏感系数ε进行讨论,同时SVR模型中核函数众多,仅选择一种核函数有一定的局限性。

本文提出利用SVR方法建立近似模型并应用于汽车的前端结构优化设计,针对SVR模型中核函数众多、核函数参数难以选择的问题,通过PSO算法对多种核函数的不同参数、惩罚系数C和不敏感系数ε进行优化并对误差进行比较,从而构造精度较高的PSO-SVR模型;以此为基础进行了某SUV的前端结构优化,在确定性优化的基础上继续进行可靠性优化,最终达到优化目的,并使优化设计结果的可靠度得到提升。

1 多目标可靠性优化设计方法

多目标确定性优化问题可以表示为:

minfa(x),a=1,2,…,Q;

s.t.gj(x)≤0,j=1,2,…,M;

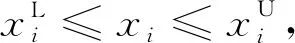
(1)

其中,fa(x)为目标函数;gj(x)为约束函数;xiL、xiU为设计变量xi的上限和下限;Q、M、N分别为目标函数、约束函数、设计变量的个数。

在基于仿真的汽车优化设计问题中,当设计变量因加工误差等外界因素发生扰动时,确定性优化设计方案有可能不满足约束条件或者目标函数对设计变量的波动极为敏感,从而使优化结果失去实际意义。

因此,对确定性优化方案进行可靠度分析来评估其可靠度是否能满足工程需求也就显得尤为重要。若其可靠度不满足要求,则需要进一步进行可靠性优化设计。多目标可靠性优化的数学模型[7]可以描述为:

minμ(fa(x)),a=1, 2,…,Q;

s.t.P(gi(x)≤0)≥Rj,j=1, 2,…,M;

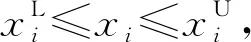
(2)

其中,μ为优化目标的均值;P(gj(x)≤0)为满足第j个约束的概率;Rj为约束函数gi(x)的可靠度需求。

在可靠性优化设计中,失效概率的表达式可以表示为:

(3)

其中,Pj为第j个约束条件的失效概率;xfx为联合概率密度函数。

计算Pj的方法有一阶可靠性方法(first order reliability method, FORM)、二阶可靠性方法(second order reliability method, SORM)和蒙特卡罗抽样估计(Monte Carto sampling, MCS)。MCS方法长期以来被认为是评估概率特性最准确的方法,因此本文在计算可靠性的过程中采用MCS方法进行抽样。

综上可得,将可靠性优化设计方法应用到汽车设计过程中,既能保证产品的经济效益,又能确保产品在实际运行中的安全可靠性。

2 PSO-SVR模型

2.1 PSO-SVR模型简介

SVR是基于统计学理论提出的支持向量机(support vector machine, SVM)推广到函数拟合中得到的[8]。SVR的基本思想是将选取的采样点数据通过非线性映射φ(x)映射到高维特征空间,并在高维空间进行线性拟合从而得到近似模型。

具体而言,对于给定的训练样本X={(xi,yi)|xi∈R，yi∈R,i=1, 2,…,n},进行拟合的目的是寻找自变量xi和因变量yi之间的依赖关系,寻找一个线性函数f(x)最小化训练样本处的预测误差,该函数可以表示为:

f(x)=ωTφ(x)+b

(4)

其中,φ(x)为一组非线性转换;ω为权重向量,ω范围越小,SVR模型的复杂度越小;b为偏差值。

s.t.yi-ωiφ(xi)-b≤ε+ξi,

(5)

其中,ε为不敏感系数;C为惩罚系数,且C>0,其控制超出误差ε样本的惩罚程度。在高维特征空间中,用核函数来代替线性问题中的内积运算,最后得到SVR的拟合函数。核函数和拟合函数分别为:

K(xi,xj)=φ(xi)φ(xj)

(6)

(7)

其中,α=[α1αi…αi…αn],α*=[α1*α2*…αi*…αn*],α、α*均为(5)式的最优解。

核函数早在20世纪60年代就被引入机器学习领域,现在已经得到广泛应用,尤其对SVM等方法而言更是不可缺少的工具。多种类型的核函数可供SVR选用,典型的核函数类型包括线性核函数、多项式核函数、高斯核函数等。文献[10]提出了一种K型核函数,并验证了该核函数具有较高的精确性和较好的泛化能力。本文克服文献[7]只对一种核函数研究的局限,综合考察多种常见的核函数,从而做出最优选择。典型核函数表达式见表1所列。

表1 典型核函数及数学表达式

2.2 PSO-SVR模型建立

PSO算法是一种用于求解单目标优化问题的优化算法,在寻优策略方面,具有收敛快、精度高、易于实现等优点。

文献[11]研究表明,应用SVR构建近似模型的精度与核函数的种类、核函数的参数选择有很大关系。

本文应用PSO算法对表1中多项式核函数参数h和参数d、高斯核函数参数s、K型核函数参数q、SVR模型中惩罚系数C和不敏感系数ε进行优化。

“扶贫先扶智”。工作队还特别重视曼来村基础教育事业的发展，通过向挂钩单位沧源县公安局统筹资金6.06万元，向社会筹措资金0.66万元，帮扶曼来小学修缮校舍，解决了教学楼房屋漏水等问题，让孩子们安心上学。

根据误差分析指标,通过比较不同核函数的精度,选择精度最高的核函数来构建描述输入与响应关系的PSO-SVR模型。近似模型的精度由确定性系数R2和最大相对误差Er判断[12],其计算表达式为:

(8)

(9)

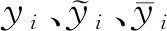
一般地,当R2≥0.9且Er≤5%时,认为近似模型具有较高的精度。

PSO-SVR模型建立的具体流程可分为以下几个步骤。

(1) 定义优化变量、目标和约束。优化问题的具体数学模型如下:

min -R2;

s.t.Er≤5%,

0.01≤C≤1 000, 0.01≤ε≤1,

0≤m≤5, 0.01≤d≤1,

0.01≤s≤5, 0≤q≤20

(10)

其中参数的取值范围由经验给出。

(2) 输入样本点和验证点的采样数据以及通过仿真计算得到的响应值,样本点和验证点数据由试验设计得到。

(3) 启动PSO算法,最大迭代次数(maximum iterations)设置为100,粒子个数(number of particles)选择50,速度最大值(maximum velocity)取0.1,共进行5 000次迭代计算。

(4) 查看优化结果,统计采用不同核函数条件下的R2、Er值。

(5) 对比不同核函数构造的PSO-SVR模型的误差,选出精度最高的近似模型应用于后续的优化。

(6) 根据多目标优化问题所定义的不同响应,依次进行上述步骤(1)～步骤(5),最终完成PSO-SVR模型的建立。

3 车辆前端结构可靠性优化设计

本文对车辆前端结构的可靠性优化设计的流程如图1所示。

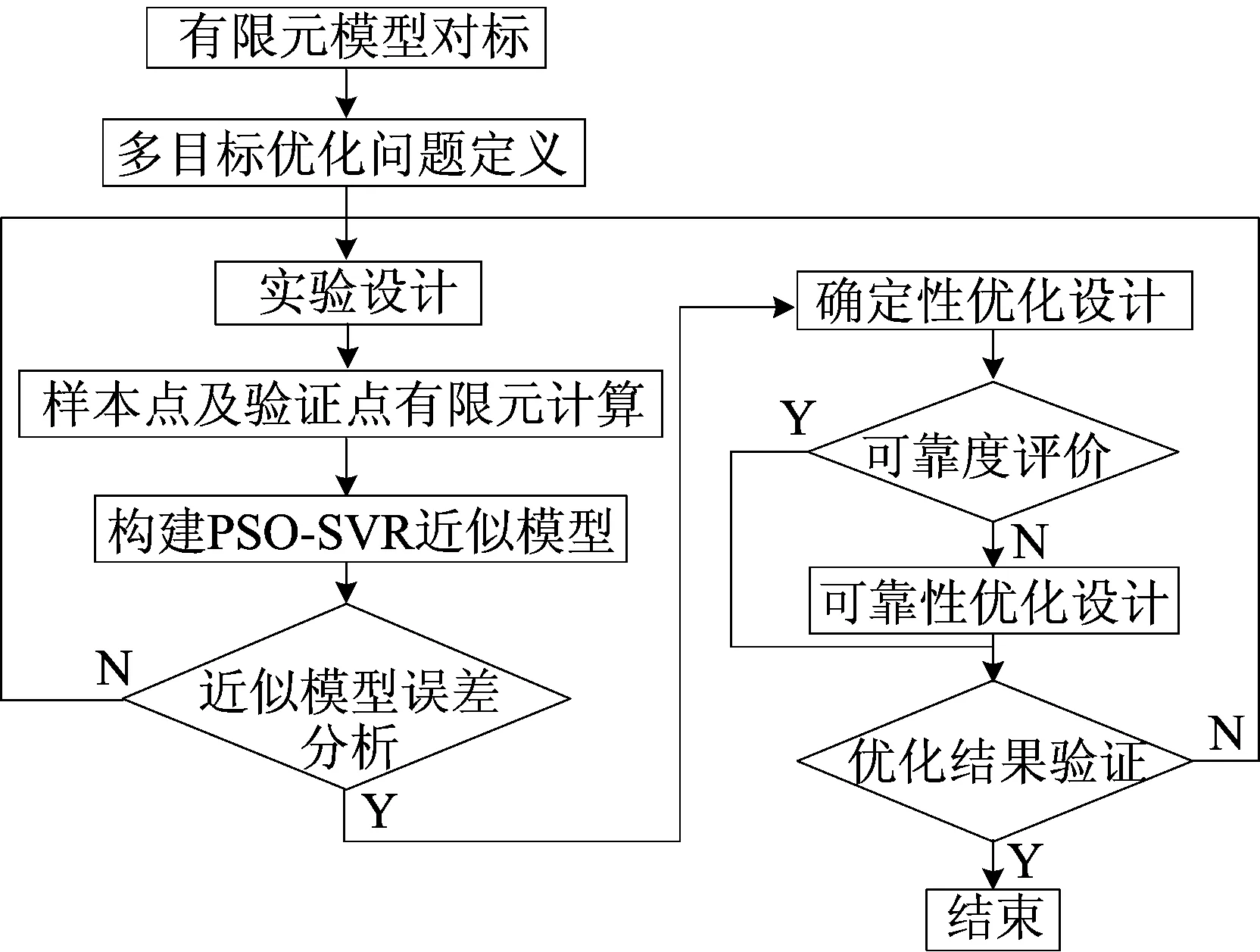
图1 可靠性优化设计流程

3.1 整车有限元模型验证

本文用作碰撞模拟的模型为某SUV,选择100%正面刚性墙壁碰撞工况进行分析。试验按照NHTSA标准释放速度为56.3 km/h。碰撞后实车试验与有限元仿真结果的对比如图2所示,整车加速度曲线的对比如图3所示,其中加速度的数值大小表示整车加速度与重力加速度g的比值。

图2 车辆正面碰撞实车试验与有限元仿真的变形对比

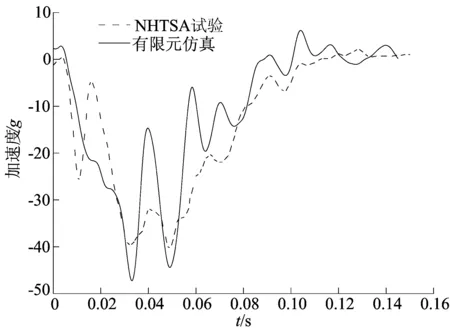
图3 正面碰撞试验与有限元仿真整车加速度的对比

由图2、图3可知,正面碰撞的实车试验与有限元仿真结果显示的车辆碰撞变形模式基本一致,加速度曲线的变化趋势基本吻合。因此有限元仿真模型具有足够的可信度,可用于后续的分析和优化设计。

3.2 多目标优化问题定义

在正面碰撞过程中,车身前端结构可以有效地吸收能量,其中主要吸能部件为前横梁、吸能盒、前纵梁等,选取合适的部件进行优化设计可以简化工作量,同时也能达到轻量化和提高安全性能的目的。针对该SUV碰撞模型,选取前防撞梁、前纵梁等8个主要吸能部件进行厚度上的优化,其厚度表示为x1、x2、x3、x4、x5、x6、x7、x8,如图4所示。

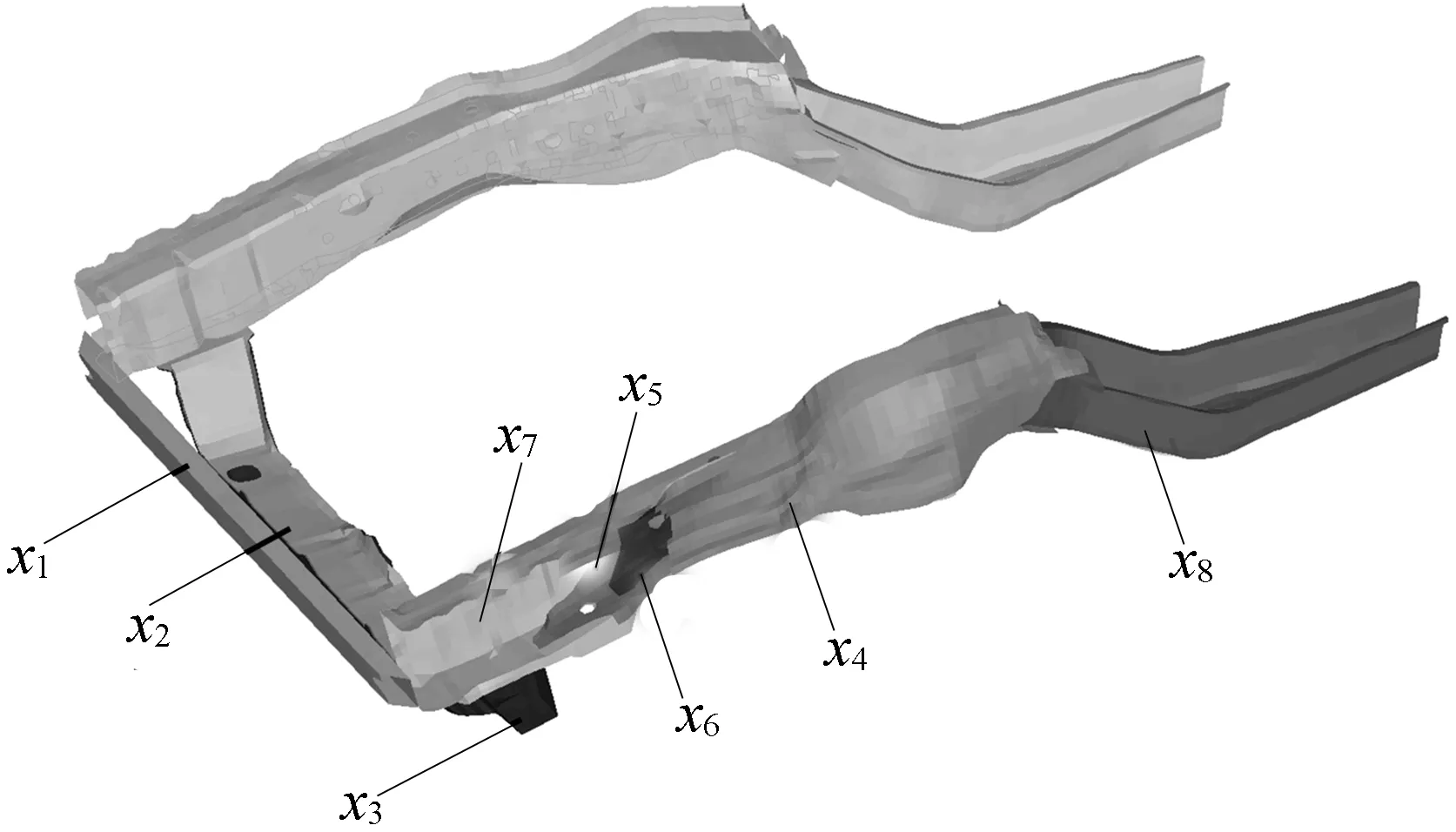
图4 优化部件分布

考虑到制造、工艺等不确定性因素的影响,假设设计变量服从正态分布,协方差系数σ/μ为0.05,变量初始设计及概率分布见表2所列。

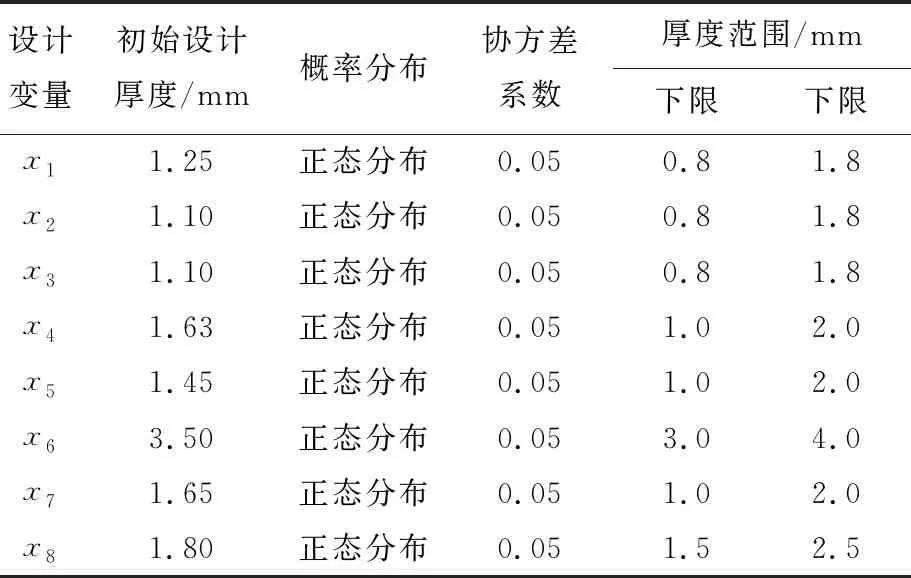
表2 变量的初始设计及概率分布

根据轻量化和提高安全性能的目标,选用优化部件的总质量m和碰撞过程中总的能量吸收EA作为优化设计目标,左后座椅附近峰值加速度a和防火墙侵入量LFI作为约束条件,响应的初始设计及优化设计目标见表3所列。

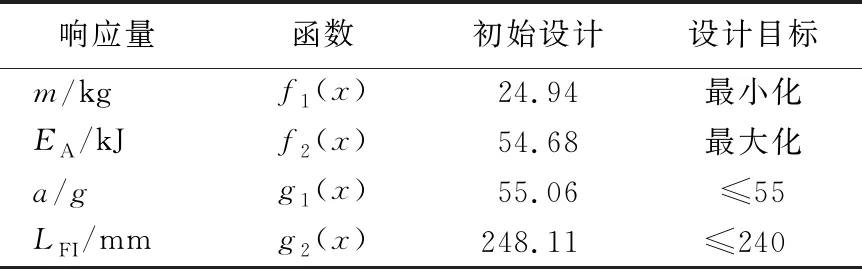
表3 响应的初始设计及设计目标

3.3 试验设计

试验设计(design of experiments, DOE)能提供合理有效的获得信息数据的方法,而样本数据的选择对近似模型的精度有很大影响。其中最优拉丁超立方(optimal Latin hypercube, OLH)试验设计方法具有非常好的填充性和均衡性。本文根据设计变量数目及设计变量的概率分布情况,在设计空间中应用2次OLH试验设计方法,生成60组样本点数据和30组验证点数据。根据DOE数据修改有限元模型中相应部件的厚度值,并测量被优化部件更新后的总质量m。将以上有限元模型提交计算机进行仿真计算,共进行90次。在后处理中提取EA、a、LFI的计算值。

3.4 核函数的选择及PSO-SVR模型建立

由DOE获得的采样点数据及仿真计算得到的响应值,针对不同的响应,应用PSO算法对参数进行优化并统计R2、Er的值,结果见表4所列。根据误差分析可知,响应EA、a可由K型核函数构造精确近似模型;响应LFI选择高斯核函数构造精确近似模型;而响应m与优化部件厚度存在线性关系,可选择线性核函数。至此PSO-SVR模型构造完毕,可用于后续优化设计。

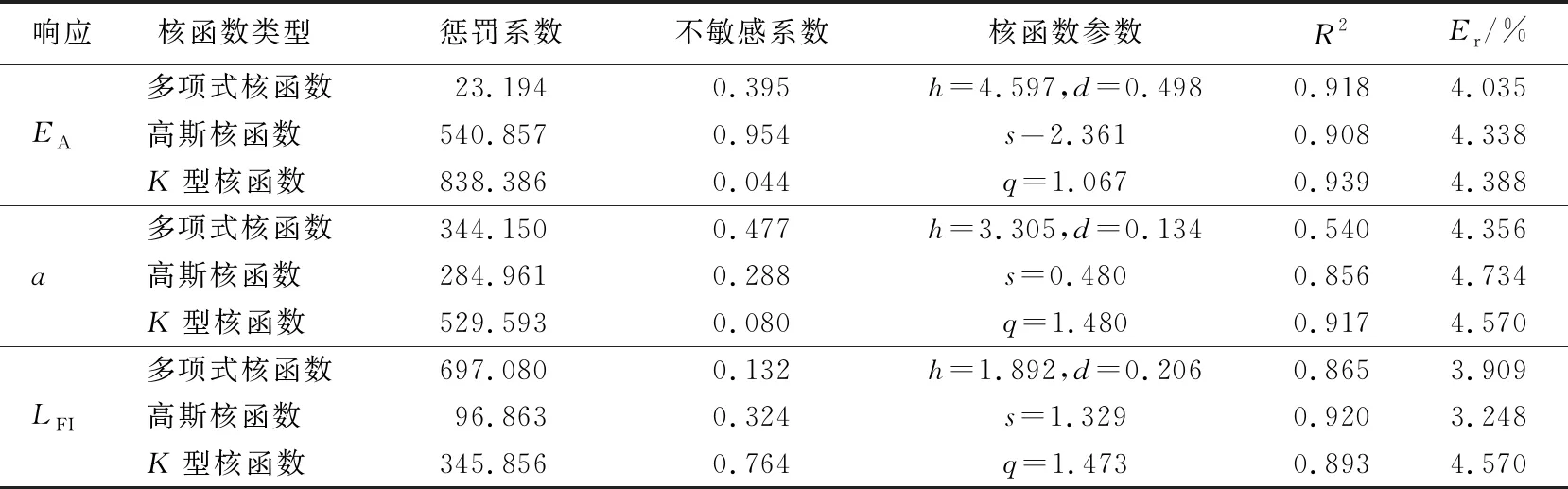
表4 核函数参数优化及误差统计

3.5 优化过程及结果分析

用上述构造的PSO-SVR模型进行优化设计,多目标确定性优化设计问题和可靠性优化设计问题的数学模型可以依次被描述为:

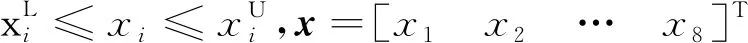
(11)

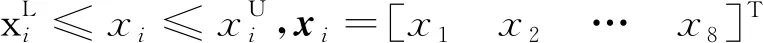
(12)

其中,R取95%和99%,即约束条件的可靠度为95%和99%以上。采用非支配排序遗传算法Ⅱ(non-dominated sorting genetic algorithm Ⅱ, NSGA-Ⅱ)迭代10 000次进行确定性和可靠性优化设计。可靠性优化设计中,分别用蒙特卡罗算法进行500、1 000次抽样并进行优化设计,优化后得到的确定性优化和可靠度为95%、99%的可靠性优化的Pareto解的前沿如图5所示。

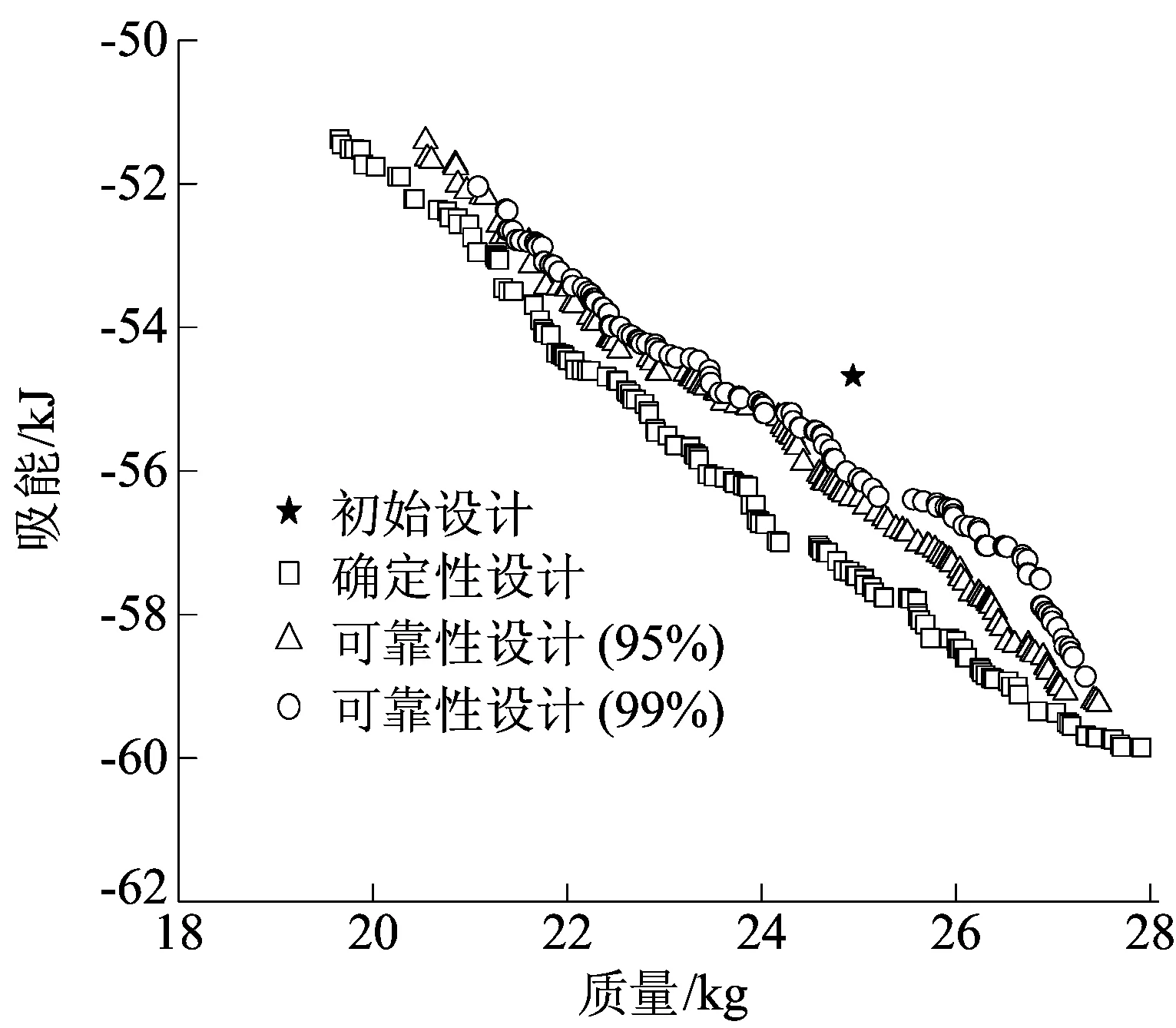
图5 确定性优化和可靠性优化设计Pareto解的前沿

从图5可以看出,可靠性优化由于考虑了设计变量不确定因素的影响,可以使设计响应远离约束边界,从而提高设计的可靠性。

采用最短距离法选择确定性优化和可靠度为95%、99%的可靠性优化的Pareto最优解,并用蒙特卡罗算法估计约束条件的可靠度,结果见表5所列。由表5可知,经过可靠性优化,约束条件的可靠度相比于确定性优化有明显提高,可靠性优化设计解结果优于确定性优化设计的解;对比可靠度为95%、99%的可靠性优化结果,可靠度为99%的优化结果虽然在设计目标m、EA上有所损失,但均优于初始设计,同时a、LFI都得到了改善,并且可靠度进一步提升。因此选择可靠度为99%的可靠性优化设计的Pareto最优解为最终设计方案。

表5 确定性和可靠性优化设计结果的对比

3.6 优化结果验证

最终优化设计方案的各变量取值见表6所列。根据表6修改有限元模型对应部件的厚度值,并提交计算机进行有限元仿真计算,初始设计与优化结果的对比见表7所列。由表7可知,近似模型的预测值与有限元仿真的计算值的最大相对误差为2.66%,最小相对误差仅0.08%,表明本文PSO-SVR模型有较高的拟合精度;与初始设计相比,优化后质量减少3.57%,峰值加速度降低5.65%,吸能和防火墙侵入量都有明显的改善,达到了轻量化和提高安全性能的设计要求,并实现了可靠性。

初始设计与优化设计的整车加速度对比如图6所示。

表6 初始和优化设计变量对比 mm

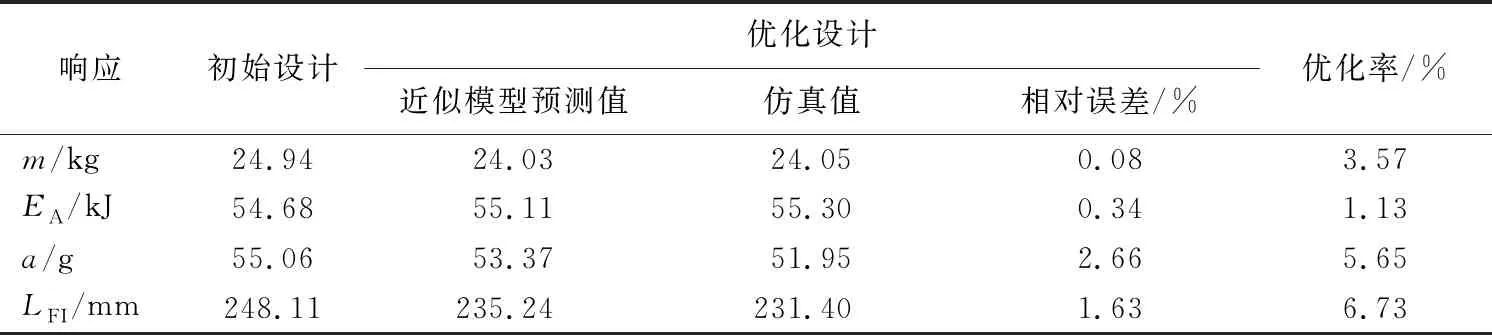
表7 初始设计与优化设计结果对比

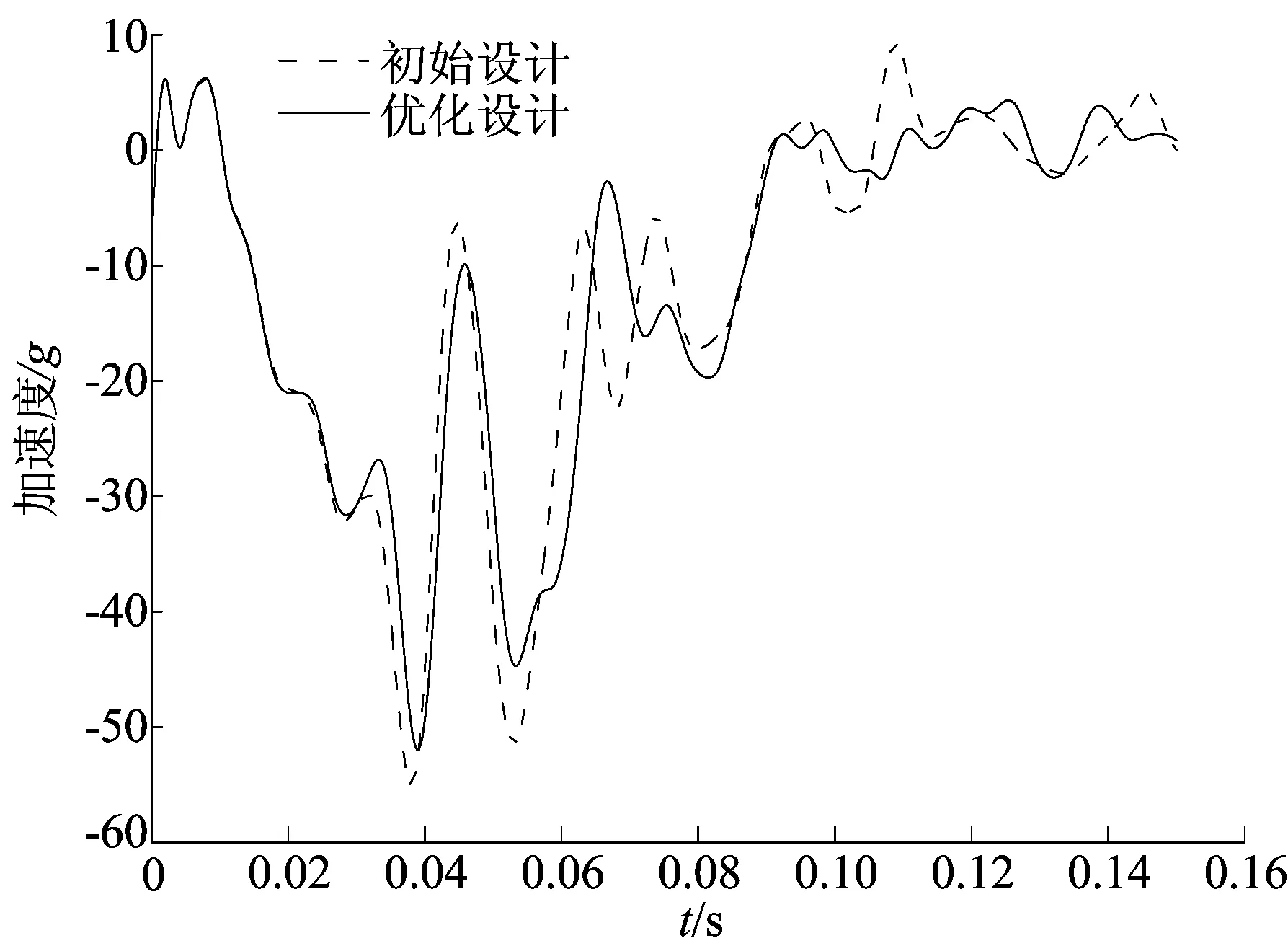
图6 初始设计与优化设计的整车加速度对比

4 结 论

(1) 本文通过PSO算法优化不同核函数参数、惩罚系数C和不敏感系数ε,根据误差分析指标选择不同的核函数,构建了精度较高的近似模型,应用于后续优化设计。

(2) 根据NHTSA正面碰撞工况进行了确定性和可靠性优化设计的比较,并选择可靠度为99%的优化设计方案为最终优化结果。与初始设

计相比,优化结果满足设计要求,其中总质量、峰值加速度、防火墙侵入量分别降低了3.57%、5.65%、6.73%,吸能增加了1.13%,同时作为约束条件的峰值加速度和防火墙侵入量的可靠度比确定性优化设计分别提高了27.30%、44.92%。