基于量子和时空混沌的图像加密方案

温贺平, 张崇富, 张 智

(1.电子科技大学中山学院 电子信息学院,广东 中山 528402; 2.电子科技大学 信息与通信工程学院,四川 成都 611731)

随着移动互联网、大数据、人工智能及5G通信等信息技术的蓬勃发展,多媒体尤其是数字图像的信息安全问题尤为引人关注[1]。数字图像具有相邻像素相关性强、冗余度高等特征,使得传统的密码体制(如DES、IDEA和AES等)面临严峻考验[2]。混沌具有对初始值和控制参数高度敏感、众态遍历性、周期点稠密等特性,与香农密码学理论中的混淆和扩散具有诸多相似之处[3]。因此,基于混沌理论的图像加密技术引起了众多研究人员的关注。经过20多年的研究与发展,混沌图像加密已成为当今的一个技术前沿和学术研究热点[4-8]。

在混沌图像加密算法中,“置换-扩散”结构作为最基本的算法结构被广泛采用[2,4-6]。文献[5]提出了一个结合Zigzag变换和三维Logistic混沌映射的数字图像加密方案,利用Zigzag变换对明文图像进行2次置换,再利用混沌序列扩散加密得到密文图像;文献[6]提出了一个基于比特平面分解的多混沌图像加密算法,采用比特级置换和扩散加密以增强算法的混淆和扩散效应。然而,由于混沌密码算法缺乏权威的安全衡量标准,这些混沌图像加密算法已被指出无法抵御密码攻击[7-8];文献[7]指出文献[5]存在安全缺陷,根据选择明文攻击,仅需较低的计算复杂度和数据复杂度即可实现算法的攻击破解。同年,文献[6]也被报道是不安全的,无法抵御已知明文攻击和选择明文攻击[8]。因此,提高混沌图像加密算法抵御密码攻击能力尤为关键,这也是决定这项技术从理论研究走向实际应用的重要因素之一。

纵观国际上混沌图像加密算法的密码分析研究,目前算法不安全的主要根源如下:一是加密方案所采用的混沌系统的安全性不足,相关研究指出低维的混沌映射复杂度不够,所产生的混沌序列存在被预估或辨识的风险[8];二是加密算法结构存在安全缺陷,无法抵御密码分析的算法攻击,如混沌密钥序列生成过程与明文无关,致使易遭受明文类密码攻击[7-8]。鉴于此,本文提出了一种基于量子混沌和时空混沌映射的图像加密方案。一方面,选取量子Logistic混沌映射和改进的耦合映像格子时空混沌系统用于生成混沌密钥序列。这2个离散混沌系统均具有较为复杂的动力学行为特性,且与连续混沌系统相比,无需离散化可有效提高算法的运行效率。因此,与其他混沌系统相比,具有良好的安全和效率性能。另一方面,为提高加密算法抵御密码攻击能力,本方案采取了明文关联生成混沌密钥序列以及密文反馈扩散加密的安全机制,提出了基于“扩散-置换-扩散”结构的混沌图像加密方案。

1 相关理论

1.1 量子Logistic混沌映射

随着量子计算等技术的发展,量子混沌引起了专家和学者的关注。量子Logistic映射作为一种典型的量子混沌[9],其所具有的更为复杂的动力学行为及量子特性引起了密码设计和分析研究人员的关注,是近年来新兴的研究热点[10-12]。

下面简要介绍量子Logistic混沌映射的工作机理。耗散量子系统与谐振子路径耦合会产生带有量子修正的量子Logistic映射。文献[9]通过反冲转子模型量化经典的Logistic映射,产生了与之对应的量子Logistic映射的迭代方程组为:

(1)

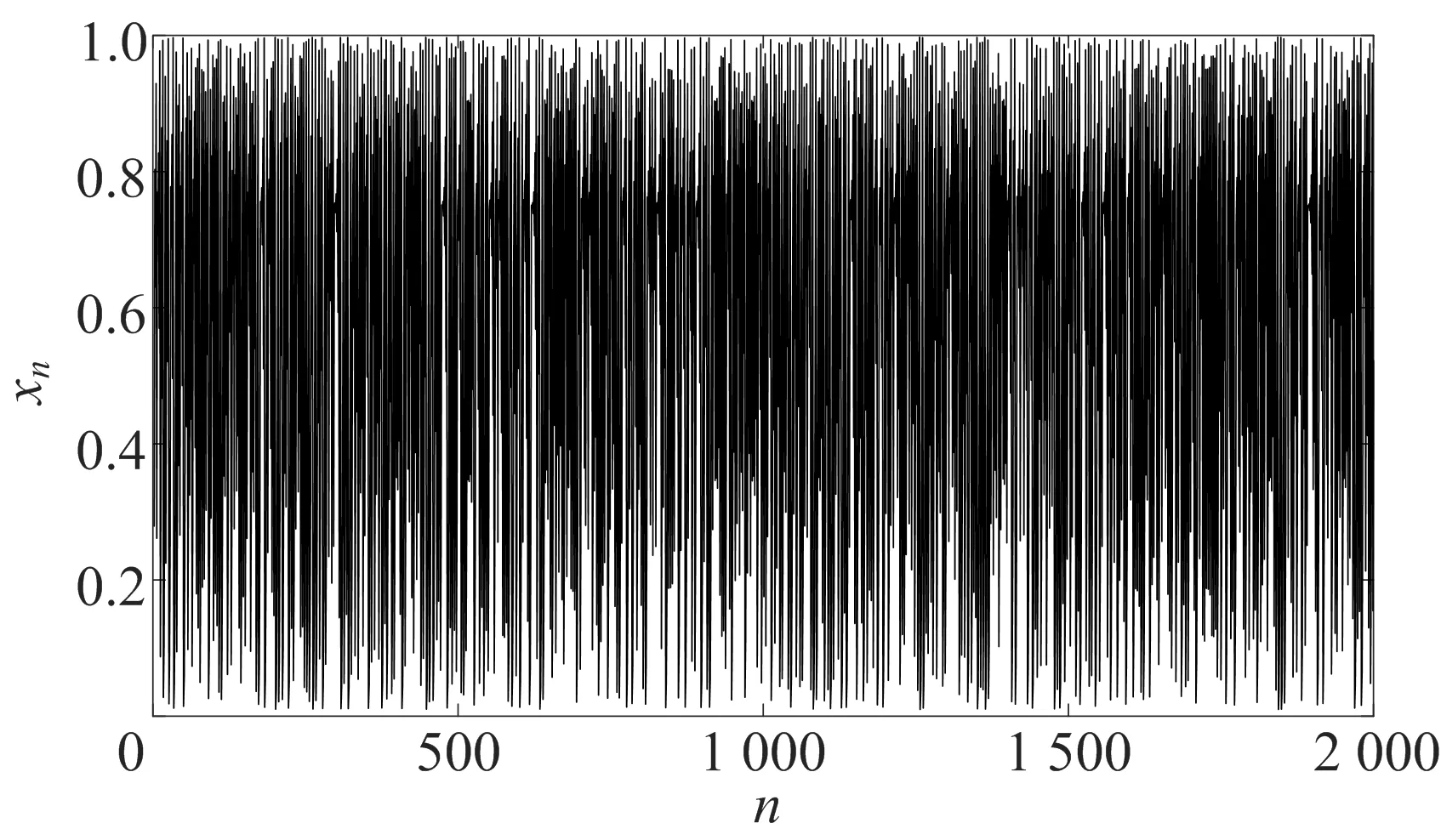
图1 量子Logistic混沌映射的迭代时序图

1.2 改进的CML时空混沌系统

混沌时空系统是指在时间和空间方向上均具有混沌行为的动力学系统。耦合映像格子(coupled map lattice，CML)是一种典型的时空混沌模型[13],具有高效率的数值仿真以及可直接利用现有的混沌理论成果,因此,CML已成为非线性动力学研究领域中一个重要的分支。

一维CML的数学模型为:

wn+1(i)=(1-ε)f(wn(i))+

ε[f(wn(i+1))+f(wn(i-1))]/2

(2)

为减少局部映射的迭代运算提高运行效率,采用简化的CML,其数学模型为:

wn+1(i)=(1-ε)f(wn(i))+εf(wn(i+1))

(3)

其中,n=1,2,…,N为离散化的时间;i=1,2,…,L为空间格子;ε∈(0,1)为耦合系数。周期性边界条件为wn(0)=wn(L)。

经典的一维CML采用Logistic作为局部混沌映射,但是Logistic混沌映射存在周期窗口等问题,安全性不足。文献[14]采用2个一维混沌映射耦合的方法生成新的一维混沌映射,理论分析表明李氏指数恒为正,具有更为复杂的动力学行为。混合Logistic和Sine混沌映射(LSS)为:

wn+1=(μwn(1-wn)+

(4-μ)sin(πwn)/4)mod1

(4)

其中,μ∈(0,4)为控制参数,在此区间内LSS的李氏指数恒为正。因此,采用LSS作为局部映射改进的CML可以表示为:

wn+1(i)=(1-ε)[(μwn(1-wn(i))+

(4-μ)sin(πwn(i))/4)mod1]+

ε[(μwn(1-wn(i+1))+

(4-μ)sin(πwn(i+1))/4)mod1]

(5)

当ε=0.8,μ=0.1,L=100,N=300时,改进的CML时空混沌系统状态如图2所示。

图2 改进的CML时空混沌系统状态图

2 图像加密方案

混沌图像加密算法通常采用经典的 “置换-扩散”的结构。置换是变换图像像素的位置而不改变图像的灰度值,在视觉上隐藏了原始明文的信息,但是它的直方图统计特性并未发生变化。而扩散是利用密钥对将置换后的像素进行替换或掩盖,它改变了图的直方图统计特性,进一步增强了图像保密的安全性能。然而,随着密码学者的深入研究发现,仅有置换的图像加密方案是不安全的,而且置换会耗费大量的系统运行时间。但不容忽视的是,置换不仅可以增强加密算法的混淆和扩散性能,而且可以提高密文图像抵御各类噪声攻击的能力。此外,基于简单替换的混淆和扩散特性不够显著,容易受到已知明文或选择明文的攻击。而采用密文反馈的扩散方式可以使得明文和密钥的信息遍历分布到所有的密文像素中,从而取得更佳的加密效果。

加密和解密过程如图3所示。

图3 加密和解密过程

基于此,本文提出了一种基于“扩散-置换-扩散”结构的混沌图像加密方案。为提高抵御密码攻击的能力,本文所提方案采取了明文关联生成混沌密钥序列以及密文反馈扩散加密的安全机制。首先将量子Logistic混沌序列对明文图像进行正向密文反馈扩散加密;然后根据改进的耦合映像格子时空混沌系统生成的密钥序列对扩散图像进行双重置换;最后再次利用量子混沌序列对置换图像进行反向密文反馈扩散加密。

加密算法的具体步骤描述如下:

(1) 明文关联的混沌映射初始条件及混沌序列的预处理。图像加密算法的密钥包括明文图像的SHA-256值、量子Logistic混沌映射和改进的CML时空混沌映射的初始值及控制参数。通过明文的SHA-256对其余混沌映射的初始值进行扰动,使得不同明文对应的密钥序列不同,从而提高抵御差分攻击的能力。具体处理方法为:

(6)

其中,x(0)、y(0)、z(0)、w(0)为量子混沌和CML映射的初始值密钥参数;x′(0)、y′(0)、z′(0)、w′(0)为通过SHA-256扰动更新后的初始值。显然,新的初始值将随不同输入的明文而发生变化。

接着,对混沌序列进行预处理。为避免混沌映射的有害暂态效应,通常丢弃前面若干个迭代序列。扩散序列由量子Logistic混沌映射产生。取量子混沌3个序列中的任意2个,以y、z为例,处理方法为:

(7)

丢弃前面l1=200个序列,K1、K2的序列长度均与图像尺寸M×N等长,分别用于正向和反向扩散加密。

扩散序列由改进的耦合映像格子生成,处理方法为:

(8)

其中,w为改进的耦合影响格子丢弃l1=100后的混沌序列,总长度为M+9N;PixRow、PixCol、BitCol分别为用sort函数生成的像素行、像素列和比特列置换的索引序列,其长度分别为M、N、8N;val1、val2、val3为排序后的混沌序列值。

(2) 正向扩散。正向扩散是采用密文反馈的方式将输入图像信息由第1个像素扩散至最后1个像素,可以表示为:

(9)

其中,I为输入的原始明文图像;C1为正向扩散后的图像;C0为正向扩散初值密钥;K1为量子混沌所产生的第1个密钥序列。

(3) 双重置换。对正向扩散加密后的图像先后采用像素级和比特级双重置换方法,具体方法如下:

(10)

其中,i=1,2,…,M,j=1,2,…,N,k=1,2,…,8N;P1、P2分别为经过像素级和比特级置换后的图像。值得指出的是,在第2轮的置换中,比特级图像是按照行不变的规则展开的,因此置换时仅针对展开后的列置换。

(4) 反向扩散。与正向扩散不同,反向扩散是采用密文反馈的方式将输入图像信息由最后1个像素扩散至第1个像素。正向和反向互相补充,进一步增强混淆和扩散特性。

(11)

C(i)=(P2(i)+K2(i))⨁K2(i)+

C(i+1)，i=MN-1,…,2,1

其中,C为最终的密文图像;Cend为反向扩散初值密钥;K2为量子混沌所产生的第2个密钥序列。

图像解密算法是加密的逆过程,步骤如下:

(1) 输入密钥参数产生混沌映射初始条件及对混沌序列的预处理。

(2) 与加密算法中反向扩散对应的逆反向扩散解密。

(12)

P2′(i)=(C′(i)-C′(i+1))⨁

K2′(i)-K2′(i),i=MN-1,…,2,1

由最终密文图像C′得到置换后的图像P2′。

(3) 与加密算法中双重置换对应的逆置换解密。与加密算法中的先像素置换再比特置换对应,解密时先进行比特反置换再像素反置换,这个步骤由置换后的图像P2′反置换得到仅正向扩散的图像C1′。

(4) 与加密算法中正向扩散对应的逆正向扩散解密。

(13)

I′(i)=(C1′(i)-C1′(i-1))⨁

K1′(i)-K1′(i)，i=2,3,…,MN

由扩散加密图像C1′还原为原始明文图像I′。通过以上分析可知,每个密文与扩散和置换密钥序列相关,而密钥序列与明文和密钥紧密关联。因此,通过算法的混淆与扩散,使得明文、密钥、密文的关系变得更为复杂,而且密文依赖于明文和密钥。当解密密钥Kd和加密密钥Ke完全匹配时,可以正确还原图像。而当密钥Ke≠Kd,即使存在微小失配也无法正确解密。

3 实验结果与分析讨论

3.1 实验环境

实验环境为Matlab R2016年,运行PC安装Windows 7 64 bit操作系统,处理器为Intel(R) Core(TM) i5-3470 CPU @ 3.20 GHz 3.60 GHz,内存8 GB。量子Logistic混沌映射的参数为r=3.99,β=6,改进的CML时空混沌系统参数为ε=0.8,μ=0.1,L=100,N=300。选取尺寸为256×256的经典Lena灰度图像作为主要的实验对象。

3.2 实验结果与分析

加密前后的图像及其直方图如图4所示。同时,本文算法与最近提出的较为典型的3种混沌加密算法进行了实验数据的对比,运行时间对比结果见表1所列。

从表1可以看出,本文算法具有更高的运行效率。

3.2.1 直方图分析

加密前后的图像直方图如图4b、图4d所示,原始图像呈现一定的统计规律,而加密的图像直方图统计特性呈现类噪声分布,很好地隐藏了图像的灰度值信息,从而提高了抵御统计分析攻击的能力。

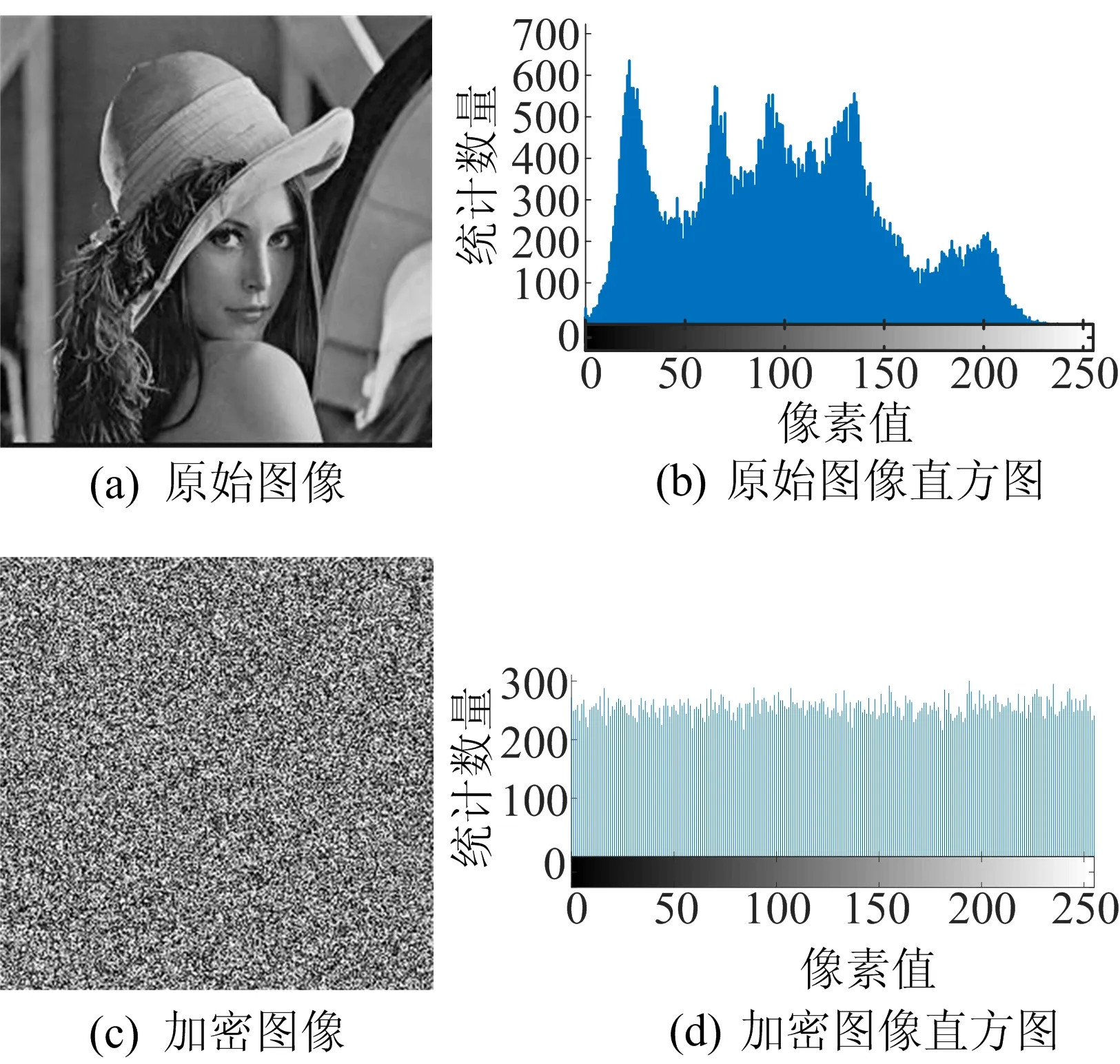
图4 加密和解密前后的图像

表1 运行时间对比 s

3.2.2 相邻像素相关性分析

通常采用相关系数来比较明文图像与密文图像的相关特性。相关系数定义如下:

(14)

其中,Cov(x,y)为图像x和y的协方差;E(x)、D(x)分别为图像x的期望和均方差。具体的实验结果如图5所示,见表2所列。

实验结果表明,明文图像在水平、垂直、对角线方向上的相邻像素点间均具有较强的相关性,而经过本文算法加密后的密文图像中的相邻像素点间的相关系数接近于0,说明不具有相关性。

图5 明文和密文图像相邻像素相关性

表2 相邻像素相关性分析

3.2.3 差分统计分析

在图像加密算法中,对明文敏感性的度量通常采用像素改变率(number of pixels change rate,NPCR)和归一化平均改变强度(unified average changing intensity,UACI)。计算公式为:

(15)

其中,M×N为图像的尺寸大小;x、x′分别为明文改变一个像素前后的密文；Dij为：

攻击者经常采用特殊的明文图像,全黑、全白和相同灰度明文图像及其直方图如图6所示。

全黑、全白、相同灰度图像对加密算法进行分析和破译,因此,具有抵御这类攻击的能力是一个优良算法所具备的必要条件。这3幅特殊明文图像经过本文算法加密后得到的密文图像及其直方图如图4c、图4d所示,验证了算法能够有效地抵御基于这些特殊的图像选择明文攻击。

此外, Lena、全黑、全白和相同灰度的密文图像的NPCR和UACI值见表3所列。

图6 全黑、全白和相同灰度明文图像及其直方图

表3 NPCR和UACI值 %

从表3可以看出其均接近理论值。因此实验结果表明,加密算法具有较强的抗差分攻击能力。

3.3 信息熵分析

信息熵是用来衡量图像信息的不确定性,通常情况下,熵值越大,信息量越大。灰度值为256的图像信息熵计算公式为：

(16)

其中,p(i)为灰度值i出现的概率。在图像加密中,希望密文图像信息熵尽可能地大。

实验结果见表4所列,经过本文算法加密后的密文信息熵接近理论值8,与同类文献相比有一定提升。

表4 密文信息熵

3.4 密钥空间

算法的密钥参数包括明文图像的哈希值、量子混沌和时空混沌映射的初值及参数。密钥空间S∈{x(0),y(0),z(0),w(0),r,μ,β,Hash 256}。假定混沌系统的初值和控制参数均为双精度类型,则这部分的密钥空间为1098。考虑到256 bit的哈希值也作为密钥,因此总的密钥长度为10175≈2581,即581 bit密钥长度。因此,在现有的计算能力条件下,能够抵抗暴力攻击。

3.5 噪声鲁棒性分析

分别在密文图像上加入5%的椒盐噪声和64×64的遮挡噪声,实验结果如图7所示。

图7 抵御常见噪声

从图7可以看出,对加噪密文图像解密后仍然可以有效辨认出图像的主要信息,验证了加密方案具有抵抗噪声攻击的鲁棒性能。

4 结 论

本文利用量子和时空混沌的复杂特性,提出了一个基于量子Logistic混沌映射和改进的耦合映像格子时空混沌映射的图像加密方案。加密方案对明文图像依次进行正向扩散、双重置换及反向扩散得到密文图像,其中所采用的明文关联和密文反馈的算法安全增强机制,提高了该加密方案抵御密码攻击的能力。实验结果表明,本文所提的加密方案具有密钥空间大、对明文和密钥敏感、密文信息熵大等特性,具有抵御暴力攻击、统计分析、差分攻击、噪声攻击等能力。与现有的混沌图像加密方法相比,在安全性能方面有所改进和增强。