3维交替方向隐式时域有限差分算法及其应用

高 林，谢国大，黄志祥，许 杰，吴先良

(安徽大学 计算智能与信号处理教育部重点实验室，安徽 合肥 230039)

随着新材料的出现和应用，与频率有关的特性材料在宽频带上的精确建模引起了现代计算电磁学领域研究人员的广泛关注[1-2]，研究人员开发了很多数值方法，以精确描述色散介质的电磁特性.基于Yee网格的时域有限差分 (finite-difference time-domain，简称 FDTD) 算法，将Maxwell方程在时间和空间上直接差分，具有简单、直观、高精度等优点，FDTD是目前使用较多的电磁计算数值算法[3].传统FDTD算法采用的是显式差分，时间步长必须满足CFL(courant-friedrich-levy)稳定条件，这个条件要求电磁波在数值网格中的计算传播速度不小于物理传播速度，时间步长的最小值由空间网格尺寸决定.在等离子体结构仿真[4]中，须采用高分辨率，然而高分辨率须网格尺寸小、时间步长小，这样就导致仿真时间长.为了消除这些限制，T.Namiki提出了无条件稳定的交替方向隐式时域有限差分 (alternating direction implicit finite-difference time-domain，简称ADI-FDTD)算法[5]，此算法把传统FDTD算法中一个时间步分解为2个子时间步,然后交替采用显式和隐式差分得到电场和磁场分量的时域步进方程.ADI-FDTD算法因具有2阶精度和无条件稳定特性，在计算电磁学中得到了广泛应用[6-8].

笔者提出一种用于精确模拟波在色散金属结构中传播的3维交替方向隐式时域有限差分算法，用广义关键点(critical points，简称CPs)模型模拟等离子体结构、研究金属材料的电磁特性.采用辅助微分方程(auxiliary differential equation，简称ADE)[9]描述电极化与电场间的本构关系，降低算法的复杂度和应用难度.最后，通过数值仿真验证算法的有效性.

1 在色散介质中的ADI-FDTD算法

1.1 色散介质中ADI-FDTD算法的Maxwell方程

差分形式的Maxwell方程组用矩阵表示为

(1)

其中：D为电通量密度；E为电场强度；H为磁感应强度；μ0为真空中的磁导系数；t为时间；矩阵A，B分别为

(2)

采用文献[5]中的ADI-FDTD算法，建立电通量密度D的更新方程.

在ADI-FDTD算法中，需要将n→n+1的时间步分解为n→n+1/2和n+1/2→n+1两个子时间分步.在n→n+1/2子时间步，对式(1)的E和H在时间和空间上进行中心差分离散，分别得到

(3)

(4)

将式(2)中的矩阵A，B代入式(3)，可得

(5)

将式(2)中的矩阵A，B代入式(4)，可得

(6)

在n+1/2→n+1子时间步，对式(1)中E和H在时间和空间上进行中心差分离散，分别得到

(7)

(8)

将式(2)的矩阵A，B代入式(7)，可得

(9)

将式(2)中的矩阵A，B代入式(8)，可得

(10)

(11)

(12)

(13)

(14)

(15)

(16)

由文献[10]可知，在色散介质中D和E间的关系为

(17)

Pm(ω)=ε0χ(ω)E(ω)，

(18)

(19)

(20)

1.2 CPs模型的辅助微分方程

近年来，多个色散模型[11-15]被提出.笔者利用CPs模型研究金属材料在光学频率下的电磁特性.文献[16]给出的磁化率表达式为

(21)

其中：φm为相位；ω为等离子体频率；Cm为振幅；Γm为增宽；Ωm为间隙能；ejφm为时谐因子，其表达式为

ejφm=cosφm+jsinφm，e-jφm=cosφm-jsinφm.

(22)

将式(22)代入式(21)，可得

(23)

将式(23)代入式(18)，得到的电极化强度P的表达式为

(24)

其中

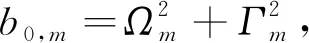
利用时域和频域间的转换关系，将式(24)转化为时域，得到的微分方程为

(25)

为避免ADI-FDTD算法出现不稳定情况[17]，笔者增加辅助变量Q, 用2个1阶微分方程替代2阶辅助微分方程.替代式(25)的2个1阶微分方程为

(26)

(27)

方程(26)，(27)在n+1/4时间步上经时域有限差分和平均离散后，分别得到

(28)

(29)

由式(28)，(29)，得到的P和Q在n+1/2时间步的差分方程为

(30)

(31)

同理，可得P和Q在n+1时间步的差分方程为

(32)

(33)

其中

fm=b1,m+4b2,m/Δt+Δtb0,m/4,f1,m=2/fm,

f2,m=-[b1,m-(4/Δt)b2,m+(Δt/4)b0,m]/fm,f3,m=[a1,m+(Δt/4)a0,m]/fm,

f4,m=[-a1,m+(Δt/4)a0,m]/fm,h1,m=b1,m-4b2,m/Δt,h2,m=b1,m+4b2,m/Δt.

(34)

式(17)中电通量密度D在n+1时间步的方程为

(35)

式(17)中的电通量密度D在n+1/2时间步的方程为

(36)

式(17)中的电通量密度D在n时间步的方程为

(37)

将式(30)代入式(36)，可得

(38)

将式(37)，(38)代入式(11)，得到的第1个子时间步Ex的时域步进方程为

(39)

将式(37)，(38)代入式(12)，得到的第1个子时间步Ey的时域步进方程为

(40)

将式(37)，(38)代入式(13)，得到的第1个子时间步Ez的时域步进方程为

(41)

将式(32)代入式(35)，可得

(42)

将式(37)，(42)代入式(14)，得到的第2个子时间步Ex时域步进方程为

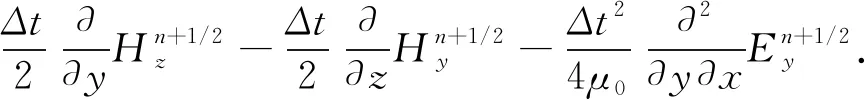
(43)

电场的其他分量同理可得.

2 数值仿真

为了验证ADI-FDTD算法模拟CPs色散介质的优越性，对典型的等离子体模型和金属谐振腔结构进行数值仿真.

2.1 具有多层金属结构的电磁波传播特性

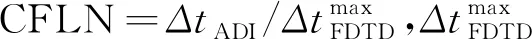
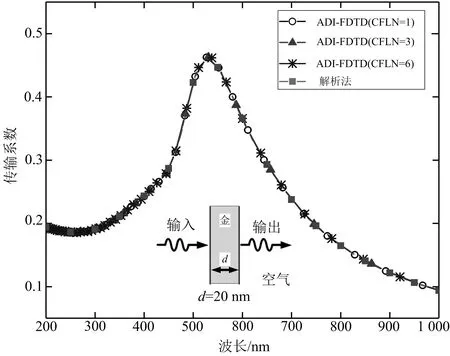
图1 解析法和3种CFLN值的ADI-FDTD算法的传输系数比较

2.2 基于矩形谐振腔结构验证ADI-FDTD算法的准确性

假定有一充满色散介质的矩形腔体，腔体尺寸为Lx=Ly=Lz=40 mm,网格大小为Δx=Δy=Δz=1 mm，网格涉及的计算区域为40×40×40，色散模型的相关参数为a0=6.989×1018s-2，a1=0,b1=6.989×108s-1，b2=1,b0=0,ε∞=1.脉冲函数为E(t)=E-(t-t0)2/(Ts)2， 其中Ts=79.6 ps，脉冲峰值出现在t=t0=4Ts时刻.图2为FDTD算法和5种不同的CFLN值的ADI-FDTD算法在探测点(3,4,4)处的电场波形图，图3为FDTD算法和5种不同的CFLN值的ADI-FDTD算法在探测点(3,3,4)处电场波形图.由图2，3可知，不同CFLN值的ADI-FDTD算法和普通FDTD算法，在同一点的电场波形基本吻合.

图2 FDTD算法和5种不同的CFLN值的ADI-FDTD算法在探测点(3,4,4)处的电场波形图

图3 FDTD算法和5种不同的CFLN值的ADI-FDTD算法在探测点(3,3,4)处电场波形图

表1为FDTD和ADI-FDTD算法的时间步、仿真时间比较，由表1可以看出，CFLN>8时ADI-FDTD算法比FDTD快.仿真结果表明：FDTD，ADI-FDTD算法占用内存大小分别为8.608 6，8.767 3 MB，即二者几乎相同.

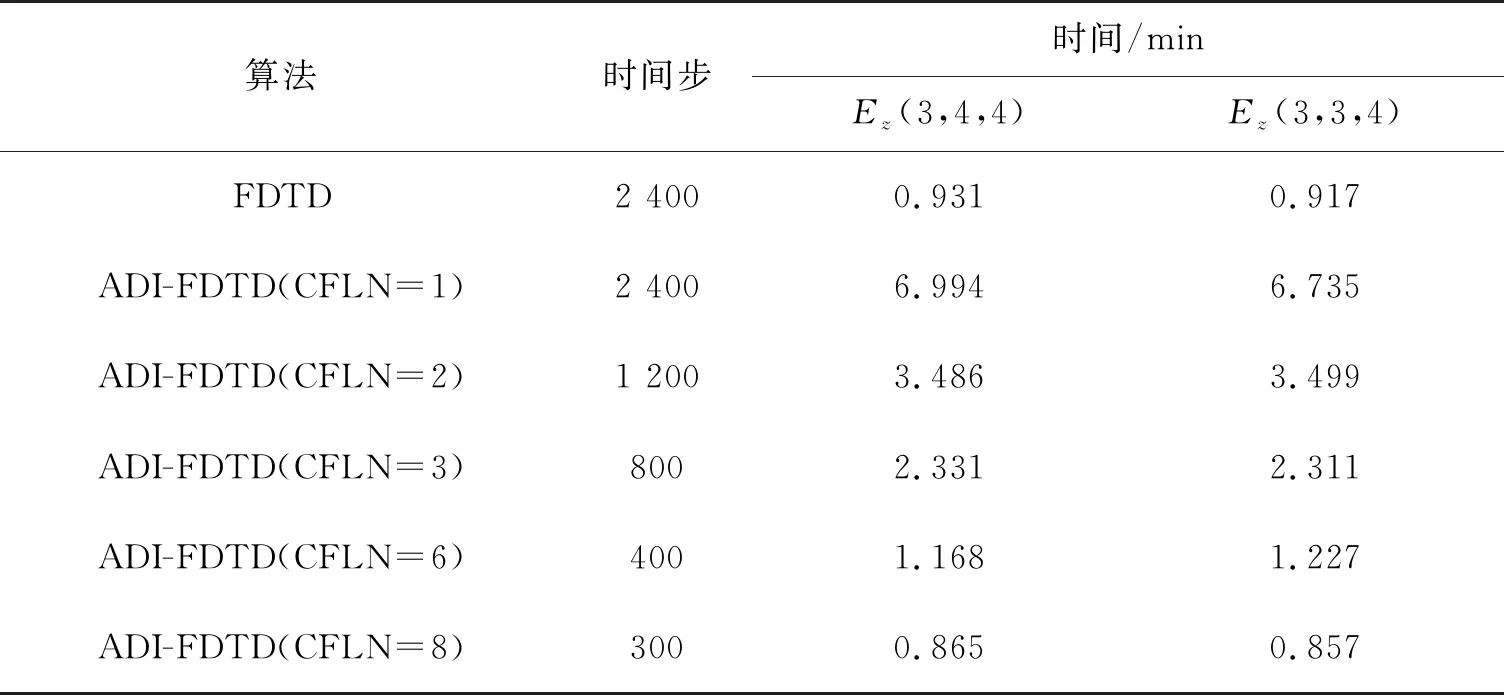
表1 FDTD和ADI-FDTD算法的时间步、仿真时间比较

3 结束语

笔者提出了一种用于精确模拟波在色散金属结构中传播的3维无条件稳定的ADI-FDTD算法.使用ADI-FDTD算法研究矩形谐振腔中的电磁波，利用基于广义CPs模型建立的辅助微分方程研究金属材料在光学频率下的电磁特性.ADI-FDTD与FDTD算法的比较结果表明，二者结果吻合较好， 但ADI-FDTD算法具有高的效率.因此，ADI-FDTD算法是替代FDTD的有效算法.