固定和增长区域上一类互惠模型的扩散动力学

林支桂，张琬婧

(扬州大学 数学科学学院，江苏 扬州 225002)

在自然界中，生物群落总是由于种种原因在不断地变化着，它是自然界里某一区域的生物所形成的一个平衡和谐的整体．种群间通过多种方式进行不断演化，其中包括互惠共生、协同竞争、寄生、捕食等，最终使得自然界达到一个相对稳定的状态[1]．物种与物种、群落和生物圈之间还存在相互制约的关系，所处环境分布的不均匀、种群的迁徙以及个体所分配到的资源不均等都会导致物种除了随时间的演化外，还会随着空间的变化而变化[2-3]．为了更好地研究物种为适应生态环境而进行的迁徙行为，人们建立了许多基于偏微分方程组的生物数学模型[4]．

Albrecht等[5]提出互惠关系的两种群模型，即论文所要研究的互惠模型

(1)

其中：u和v表示两个种群；ai(i=1,2)为种群的内禀增长率，其反映了在理想状态下生物种群的最大增长能力；bi和Ki(i=1,2)表示两种群间的相互影响关系及承载能力；ci(i=1,2)表示种群内的竞争系数．系数ai，bi，ci和Ki均为正常值．

种群的扩散与种群密度有关[6]，从而得出如下互惠扩散模型

(2)

其中：正常数d1,d2代表物种u,v的自由扩散系数．

实际上，种群的栖息地是随时间不断变化的，例如我国鄱阳湖水域面积随季节变化而变化，冬季水域面积明显小于夏季水域面积[7]，最小值出现在1月中下旬，最大值出现在8月上旬，其面积变化超过3倍.这种区域的变化也会影响方程(组)解的长时间性态．近年来，区域的增长对种群发展演化的影响引起了人们的关注[8-9]．因此，论文在固定和增长区域两个方面考虑互惠扩散模型的动力学．

1 固定区域上的互惠模型

在(2)式的基础上，给出在齐次Neumann边界条件下固定区域上的互惠扩散模型

(3)

其中：η是∂Ω上的单位外法向量；u0(x)和v0(x)是非负有界函数；Ω⊂Rn为有界区域，其边界∂Ω光滑．

由偏微分方程理论，易知系统(3)的局部解存在唯一，又通过比较原理[10]，得其有界性和全局存在性．

(4)

定理2平凡解(0,0)是不稳定的．

证明首先将方程(3)在(0,0)处线性化，得

(5)

令u=eλtφ，v=eλtψ，代入(5)式得

取特征函数φ=1，ψ=0，得到λ1=a1>0；取φ=0，ψ=1，得到λ2=a2>0.由局部稳定性定理可知平凡解(0,0)是不稳定的．

定理3半平凡解(uΔ,0)和(0,vΔ)均是不稳定的．

证明首先证明半平凡解(uΔ,0)是不稳定的．

令U=u-uΔ，V=v-0，将方程(3)在(u,v)=(uΔ,0)处线性化，得

(6)

相同地，令U=eλtφ，V=eλtψ，代入(6)式得特征问题

定理4正平衡解(u*,v*)是全局渐近稳定的.

证明先给定一个t0>0，得u(x,t0)>0,v(x,t0)>0，故可以取得δ>0且充分小，满足

(7)

取(M1,M2)满足

(8)

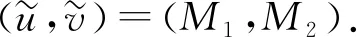
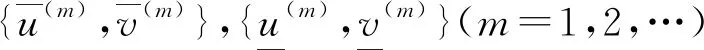
(9)

由正性引理，易知上述序列的单调性质

再由单调有界定理，可知此序列的极限

存在，且满足

在问题(9)中令m→∞，则

(10)

2 增长区域上的互惠模型

考虑增长区域上具Dirichlet边界条件的互惠扩散模型，探究栖息地的演化对种群生存的影响．假设区域Ω(t)随时间增长，根据质量守恒定律和Reynolds输运定理，再利用Fick扩散定律，得演化区域Ω(t)上的互惠扩散模型

(11)

由于问题(11)中的方程含有对流项和稀释项，故研究此问题解的长期性态有一定的困难．类似文献[11]，利用Lagrangian坐标变化，笔者设法将一个连续演化的区域Ω(t)转变为一个固定的区域Ω(0)．

假设区域Ω(t)的增长是各向同性的[12]，亦即区域Ω(t)随着时间的增加在所有方向上同比例增长，数学上表示为

x(t)=ρ(t)y,y∈Ω(0),

(12)

(13)

这是论文要进一步研究的新的互惠扩散模型．

将问题(13)在(0,0)处线性化，得

(14)

(15)

同样地，对于问题(14)中的第2个方程，其相应的特征值问题为

(16)

显然当di>0且ai(i=1,2)，ρ∞均是常值时，问题(15)，(16)必有唯一的主特征值Ru(>0)和Rv(>0)，并且其对应的特征函数φ(y,t)和ψ(y,t)是正有界的．为了进一步强调Ru，Rv对于系数di，ρ∞的依赖性，记Ru=Ru(d1,ρ∞)，Rv=Rv(d2,ρ∞)，称之为生态再生指数．

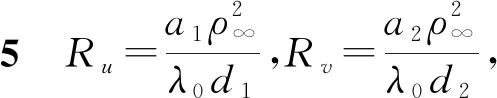
证明设(λ0,φ(y))是特征值问题

(17)

的主特征值和特征函数．

(18)

(19)

定理得证．

观察式(18)，(19)，显然Ru和Rv分别是di(i=1,2)的单调减函数，是ρ∞的单调增函数．

例取a1=2.79，a2=2.4，得

周期演化下的稳定状态如图1所示.

(a)，(b)分别表示物种u和v在增长区域上最终将稳定于一个正平衡解;(c)表示在增长区域上种群的分布情况，彩色条表示 的是种群的密度;(d)表示模型(13)的解收敛于一个稳定态(红色虚线). 图1 周期演化下的稳定状态

由图1可知，在区域增长的情况下，Ru>1且Rv>1时，物种u和v不断繁衍进化，最终趋于一个稳定规模.

3 结束语