基于AHSVM-WOA的钢板表面缺陷分类算法

冯 瑶，储茂祥，邓 鑫，齐新雨

(辽宁科技大学 电子与信息工程学院，辽宁 鞍山 114051)

钢板表面在生产过程中受设备、工艺、环境等因素影响，出现多种类型的缺陷[1]，如麻点、划伤等.为此，钢铁企业采用表面检测系统[2]来监控钢板的表面缺陷.机器学习模型已用于数字图像的处理[3]及工业产品的检查、预测和识别[4-7].在钢板表面检测领域，支持向量机(support vector machine, 简称SVM)[5-7]的模型广泛应用于缺陷分类识别，取得了良好的效果.文献[6]虽然在缺陷分类精度方面有一定的效果，但其分类是针对理想化的缺陷样本集的，忽略了集合中存在的标签和特征噪声.文献[7]通过引入权重抑制了远离缺陷样本区域的标签噪声，但忽略了靠近缺陷样本区域的特征噪声对分类结果的影响.在模式识别领域，提出了孪生超球体支持向量机(twin-hypersphere support vector machine, 简称THSVM)[8-9]分类模型，该模型具有分类速度快、精度高、无矩阵求逆、泛化性能好的优点.

为解决钢板表面缺陷的标签和特征噪声问题，笔者在THSVM的基础上提出一种抗噪声的超球体支持向量机(anti-noise hypersphere support vector machine, 简称AHSVM)分类模型.为提高钢板表面缺陷的分类效果，提出AHSVM与鲸鱼优化算法(whale optimization algorithm, 简称WOA)[10]结合的AHSVM-WOA算法.

1 AHSVM分类模型

1.1 模型描述

使得

(1)

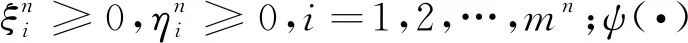
AHSVM分类模型具有如下属性：

(1) THSVM是一个2分类模型，需要结合多分类技术实现分类. AHSVM分类模型针对N种类型的缺陷构造了N个超球体，其自身就是一个多分类模型.

(2) THSVM通过少量边界缺陷样本构造超球体，特征噪声主要分布在缺陷样本集合区域附近，很容易成为边界缺陷样本，从而影响THSVM，而AHSVM构造的超球体改变了THSVM仅依赖少量边界缺陷样本的策略.对于AHSVM，约束条件第1项使超球体外部的缺陷样本被用，约束条件第2项使超球体内部的缺陷样本被用，这意味着AHSVM构造的超球体使用了所有的缺陷样本，特征噪声对依赖所有缺陷样本的AHSVM难以产生影响.

(2)

1.2 模型求解

为了求解式(1)，引入拉格朗日函数

(3)

根据库恩-塔克(Karush-Kuhn-Tucker, 简称KKT)条件，可得

(4)

使得

(5)

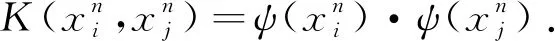
(6)

根据优化结果，得到超球体的参数为

(7)

其中：|Ωn|为边界上缺陷样本的数量.

给定一个缺陷样本x，其决策函数可表示为

(8)

2 AHSVM-WOA算法

AHSVM分类模型中的ν1，ν2，σ2通常采用网格搜索法进行选择，但网格搜索法速度慢，运行时间长.文献[11]将粒子群优化算法与SVM结合选择参数，加快了搜索速度，但粒子群优化算法易陷入局部最优.为了解决此问题，笔者将AHSVM与WOA结合优化参数，可有效避免局部最优，且搜索速度更快.

2.1 WOA

WOA是文献[10]提出的模仿座头鲸捕食行为的一种新型优化算法.在捕食过程中，座头鲸通过收缩包围及螺旋机制，不断更新自身位置，实现快速捕食.座头鲸捕食机制的数学模型为：

当p<0.5,|A|<1时，有

(9)

当p<0.5,|A|≥1时，有

(10)

当p≥0.5时，有

(11)

其中：p为[0,1]中的随机数，p<0.5对应收缩包围机制，p≥0.5对应螺旋机制；A=2as1-a,B=2s2,a=2-2t/Tmax,t为当前迭代次数，Tmax为最大迭代次数，s1和s2为(0,1)中的随机数；当A<1时，鲸鱼对目标发起攻击；当A≥1时，随机选择一头鲸鱼位置作为最优解来更新其他鲸鱼的位置；D为收缩包围机制下鲸鱼与目标间的距离；Y(t)为鲸鱼的当前位置，Y*(t)为鲸鱼当前的最好位置，Y(t)rand为随机选择的鲸鱼位置；Dp表示螺旋机制下鲸鱼与目标间的距离；l为(-1,1)中的随机数；b=1.

2.2 算法流程

分类精度通过适应度描述，适应度的表达式为

(12)

AHSVM-WOA算法的步骤如下：

(1) 参数初始化，ν1∈[1,100],ν2∈[0,1],σ2∈[1,150]，种群维度d=3，最大迭代次数Tmax=10，种群规模设为20，鲸鱼的初始位置随机产生；

(2) 将初始位置代入AHSVM分类模型，通过训练和测试得到适应度；

(3) 随机选择p，r1，r2，根据位置更新策略，对种群位置进行更新；

(4) 位置更新后，重新计算适应度，并与上次适应度进行比较，如果当前更优，则保留当前适应度；

(5) 如果达到最大迭代次数，则输出当前最优适应度，否则，返回(3)继续迭代，直到满足最大迭代次数.

3 钢板表面缺陷分类实验

为了验证AHSVM-WOA算法的抗噪性能，该文采用文献[12]中的热轧钢表面缺陷数据库进行实验.该数据库有6类的缺陷图像，它们为：裂纹、夹杂、斑块、麻点、氧化铁皮、划伤，如图1所示.

图1 热轧钢板的6类表面缺陷图像

通过缺陷分割提取和特征描述，共获缺陷样本3 718个，裂纹、夹杂、斑块、麻点、氧化铁皮、划伤缺陷样本数分别为 672，699，726，473，611，537.特征类型有： 3种几何特征、7种不变矩特征、9种灰度特征、16种纹理特征[13]，每个缺陷样本均为1个35维的向量.缺陷样本被划分为训练集和测试集，用于分类的训练和测试. 从分类精度角度，比较AHSVM-WOA、SVM、TSVM、THSVM算法的抗噪性能.针对原始缺陷样本集，4种算法的分类精度如表1所示.

表1 4种算法对原始缺陷样本集的分类精度 %

从表1可知:对斑块、麻点和氧化铁皮缺陷，AHSVM-WOA分类精度均达到了100%，SVM，TSVM，THSVM分类精度均小于100%；对于裂纹和夹杂缺陷类型，AHSVM-WOA分类精度分别达到了98.52%和97.14%，仅次于TSVM；对于划伤缺陷类型，AHSVM-WOA分类精度达到了93.46%，仅次于THSVM.

表2展示了分别加入5%标签噪声后缺陷样本集的分类精度与表1对应分类精度的差.

表2 4种算法对有标签噪声的缺陷样本集的分类精度差 %

从表2可知:对裂纹、夹杂和斑块缺陷，AHSVM-WOA分类精度分别降低了0.01%，1.43%，2.74%，相对于SVM，TSVM，THSVM，AHSVM-WOA分类精度降低最少；对氧化铁皮缺陷，AHSVM-WOA分类精度降低了8.42%，而SVM，TSVM，THSVM分别降低了5.64%，7.81%，4.68%；对划伤缺陷，AHSVM-WOA的分类精度无变化，而SVM，TSVM，THSVM分别降低了1.44%，2.325%，5.09%.

表3展示了分别加入5%特征噪声后缺陷样本集的分类精度与表1对应分类精度的差.

表3 4种算法对有特征噪声的缺陷样本集的分类精度差 %

从表3可知:对裂纹、斑块和氧化铁皮缺陷，AHSVM-WOA分类精度分别降低了2.71%，2.45%，2.92%，相对于SVM，TSVM，THSVM，AHSVM-WOA分类精度降低最少；对夹杂缺陷，AHSVM-WOA分类精度无变化，而SVM，TSVM，THSVM分别降低了4.69%，8.90%，3.13%；对划伤缺陷，AHSVM-WOA分类精度降低了0.26%，而SVM，TSVM，THSVM分别降低了2.05%，0.24%，0.74%，仅次于TSVM.

表4为混合加入4%标签和4%特征噪声后缺陷样本集的分类精度与表1中分类精度的差.

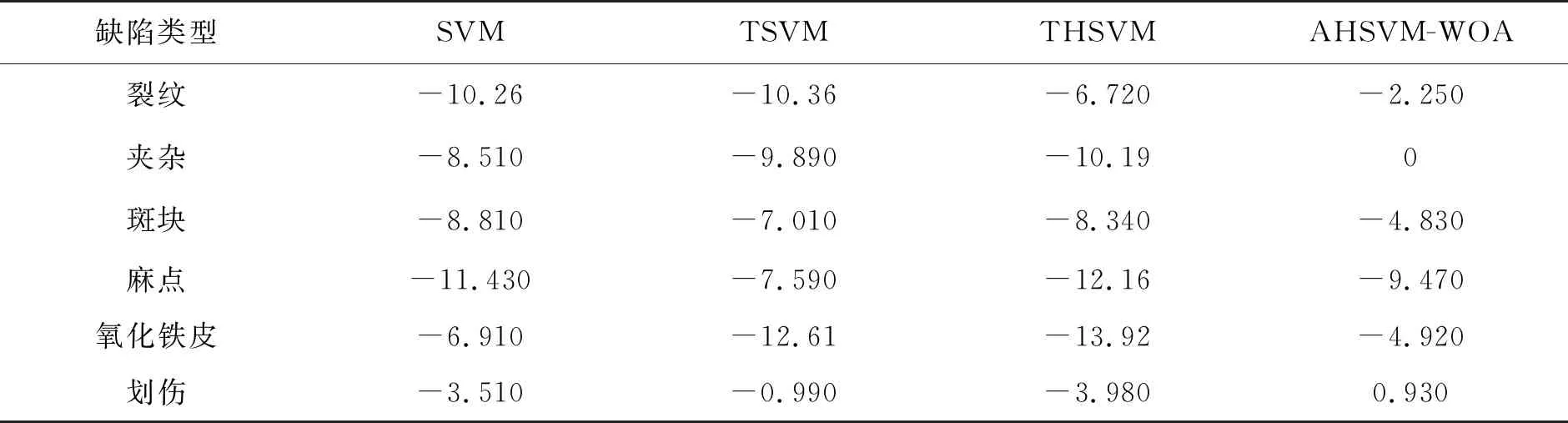
表4 4种算法对有标签和特征噪声的缺陷样本集的分类精度差 %

由表4可看出:对氧化铁皮缺陷，受噪声影响最小的还是AHSVM-WOA，分类精度只降低了4.92%,而SVM，TSVM，THSVM分别降低了6.91%，12.61%，13.92%；对裂纹、夹杂和斑块缺陷，AHSVM-WOA受噪声影响最小；对麻点缺陷，AHSVM-WOA受噪声影响不是最小但也不是最大，仅次于TSVM.

图2展示了SVM，TSVM，THSVM，AHSVM-WOA的总分类精度.由图2可以看出，与其他算法相比，AHSVM-WOA的分类效果最优且波动最小.

图2 4种算法对有不同噪声的缺陷样本集的总分类精度

图3展示了AHSVM结合网格搜索、粒子群优化及鲸鱼优化选择参数时的分类精度、迭代次数和运行时间.由图3可看出:在分类精度上，鲸鱼优化与网格搜索几乎相同，粒子群优化效果最差；在迭代次数上，鲸鱼优化最少；在运行时间上，网格搜索是鲸鱼优化的4.8倍，粒子群优化是鲸鱼优化的2.2倍.

图3 AHSVM结合网格搜索、粒子群优化及鲸鱼优化选择参数时的分类精度、迭代次数及运行时间

综上，与SVM、TSVM和THSVM相比较，AHSVM-WOA分类算法具有好的分类效果，且有良好的抗噪声能力.同时，AHSVM-WOA算法选择参数缩短了运行时间，提高了效率.

4 结束语

笔者提出的AHSVM分类模型通过引入核密度估计信息，能抑制标签噪声.同时，AHSVM改变了依靠少量边界缺陷样本的策略，利用所有样本生成超球体，能抑制特征噪声.将AHSVM与WOA结合，避免了陷入局部最优，提高了计算效率.将AHSVM-WOA算法应用于6类钢板表面缺陷分类，获得了较好的分类结果，说明该算法具有有效性.后续研究应考虑对缺陷样本进行稀疏处理，节省存储空间，进一步提高运行效率，实现更好的分类效果.