基于核密度估计密度峰聚类的通信辐射源个体识别

李 昕， 雷迎科

(国防科技大学电子对抗学院,合肥,230037)

通信辐射源个体识别是通过信号携带能够反映发射机差异的信息及特征，来判别信号与发射机之间的从属关系的，即通过信号区分发射机[1]。通信辐射源个体识别最早应用于军事通信领域[2]，并取得了较大的发展；最近随着新技术的发展，它在认知无线电[3]及自组织网络中扮演着越来越重要的作用[4]。

基于发射机的工作模式，通信辐射源个体识别使用的信号被分为瞬态信号和稳态信号。瞬态信号一般被称为“turn-on”信号，能够提供适合特征提取及发射器识别的独特且可区分的特性[5-6]。为了测量瞬态特征，主要方法是在噪声中检测瞬态信号的起点和终点[7]并提取它。瞬态特征基本上与发射机是一致的，这有利于识别；但瞬态信号持续时间较短，难以提取，且瞬态特征易受到非理想和复杂信道的影响，会造成识别结果不准确[8]。

稳态信号是发射机处于稳定工作状态下发射的信号，尽管稳态特征倾向于被传输信息的破坏程度，但对稳态信号的研究仍然有实际意义，因为稳态信号容易被检测和捕捉。在这种条件下很多特征提取方案已经被提出，例如双谱特征[9]和生物启发特征[10]。在这些方案中，使用的最为广泛的是基于信号时频表示的特征，时频表示是将信号映射到时间和频率的二维平面上，同时提供时间和光谱信息。文献[11]提出了一种基于短时傅里叶变换(STFT)的信号检测和识别系统，然而短时傅里叶系统是一种线性变换，不能用于分析非线性信号。文献[12]利用Winger和Choi-William分布提出了类似雷达波形识别算法。文献[13]使用了基于二次时频表示和顺序分类器的辐射源识别方案。XU[14]于2007年提出基于信号杂散特征识别电台的方法，可以识别同类型的电台个体，但在低信噪比条件下识别率不高。唐智灵[15]在2013年对杂散特征进行研究，在实际信号的数据集上验证了算法性能的可靠性。梁江海[16]利用经验模态分解模型，从时域和频域分析电台信号进行识别。韩洁等研究人员[17]在2017年提出将信号转换成3D-Hibert能量谱，在一定程度上实现了基于少量样本对通信电台个体的识别。唐哲等研究人员[18]提出利用矩形积分双谱特征和基于最大相关熵的通信辐射源识别方法。黄健航等研究人员[19]提出在小样本条件下基于自编码网络的通信辐射源个体识别方法。

以上提出的通信辐射源个体识别方法都需要充裕的已知类别信息的信号样本，然而在实际复杂的电磁环境中，人们很难获得充裕的已知类别信息的辐射源观测样本数据。即在实际复杂电磁环境下，常常面临的是大规模、没有类别信息的通信辐射源观测样本数据。如果直接采用上述提出的基于有类别信息的充裕样本的监督机器学习方法或者半监督机器学习方法，其识别性能必将受到影响。本文采用无监督机器学习中的聚类河源方法进行通信辐射源个体识别。

2014年，Alex Rodriguez和Alessandro Laio提出了基于密度峰值聚类(Density Peaks Clustering，DPC)的算法[20]。DPC算法可以在无监督条件下对数据进行聚类，且算法简单高效，具有较好的识别效果。但DPC算法的识别效果受给定的数据库和挑选的参数dc(截断距离)影响。dc主要用来计算各个点的密度并识别每个类的边界点。对于不同的数据集，DPC使用不同的方法去估计密度且参数dc的取决于主观经验。为了克服这个问题，本文采用基于核密度估计的方法改善DPC算法。本文提出的方法是一种基于热扩散方程[21]用于估计给定数据集概率分布的非参数方法，该方法是基于在无限域中的热扩散，考虑到了截断距离的选择和核密度估计的边界校正。

本文提出的基于改进的密度峰值聚类的通信辐射源个体识别方法能够在无监督条件下进行通信辐射源个体识别，并解决已知类别信息的信号样本数量不足问题；针对DPC算法识别效果依赖于人工输入参数dc，在球形数据集上聚类性能不佳的问题，利用热扩散方程中时间参数t计算数各据点的密度和寻找各簇的边界，实现参数自适应，在不需要人工输入参数dc时在各个数据集上都有较好的表现。

1 DPC算法

DPC算法能够通过快速搜索聚类中心的方法来创建任意形状的簇，该算法认为作为聚类中心的数据点具有较高的局部密度ρ，与非聚类中心点相比，到其他聚类中心点的距离d更大。因此对于数据点i，DPC算法需要计算局部密度ρi以及点i到最近的且密度比其大的点的距离δi。具体步骤如下：

1)计算局部密度ρi。

(1)

其中：

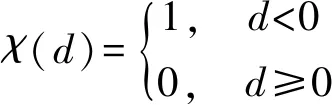
(2)

式中：dij表示点i到点j的距离；dc为截断距离；ρi为距点i距离小于dc点的数量。因此，dc在计算每个点的局部密度时是必不可少的参数，DPC算法的性能也取决于参数dc的选取。对于小的数据集，ρi可能会受到较大的统计误差的影响，因此本文采用非参数核密度估计方法[22]计算各个点的局部密度。

2)计算相对距离δi。

(3)

式中：δi的定义是数据点i到其最近的且局部密度比其大的数据点的距离，如果数据点i是密度最大的点，则δi为点i到其它点距离的最大值。

3)寻找聚类中心点。

聚类中心点具有较高的局部密度以及较大的相对距离，因此，计算完各个数据点的局部密度ρi和相对距离δi后，以ρ和δ为坐标轴建立二维平面直角坐标系，各个数据点根据各自的ρi值和δi值放置在该坐标系中，形成二维平面图被称为决策图。如图1(a)所示，28个数据点按密度递减顺序排列，图1(b)是相对应的这28个点形成的决策图。点1和10具有较高的ρ值和δ值，这是聚类中心点的典型特征。因为点26,27和28是孤立的，它们具有高δ和低ρ，可以被认为是噪声或异常值。因此，使用决策图，可以很容易地识别聚类中心点。在成功找出聚类中心点后，DPC会根据δ值将剩余数据点分配到最近的聚类中心。

4)寻找边界区域。

归属于一个簇的数据点也在另一个聚类中心点的距离小于dc，这类点的集合被称为该簇的边界区域。对于这些边界点，DPC在的边界区域内找到具有最大密度点的密度为ρb，密度高于ρb的那些点被认为是聚类点，而其他数据点被识别为簇晕点或者噪音。

2 基于热传播的密度峰值聚类

2.1 核密度估计

(4)

高斯核K(x;xj;h)经常被用做估计密度。

(5)

式中：K是按照1/h缩放的核函数；h是核函数的带宽。

式(4)的性能很大程度上依赖于对带宽h的选择[26-27]。积分均方误差(Mean Integrated Squared Error，MISE)[21]是用于确定h的最佳值的工具之一，如式(6)所示：

(6)

但是高斯核密度估计存在以下问题：①参数h(带宽)难以选择；②存在边界误差；③平滑不足或者过度平滑。

2.2 改进后的核密度估计

不同于式(1)和(4)的方法，本文采用热扩散方程[21]进行核密度估计。热扩散方法将核密度估计视为扩散偏微分方程的唯一解，其时间参数t与核带宽h意义一致[28-29]。通过热扩散方程对KDE的解释源于维纳过程——对于一个连续时间随机过程，其下一阶段可以由前一状态直接计算，具体解释如下所示：

1)n个均匀分布的l维数据点{x1,x2,…,xn}；

2)采用高斯核计算从点xi到xj的转移概率：

(7)

核密度估计在式(7)中被解释为在该过程中与时间t有关的概率密度分布函数，参数t与式(5)中的参数h一致。

(8)

式(8)是一个迭代过程，因此这个转变满足偏微分方程。

(9)

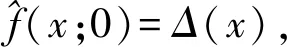
(10)

式中：Xl和Xu是域对应的上限和下限。考虑到Neumann边界条件和数据点的概率密度在[0,1]内，因此这个偏微分方程的解可以用θ核(θ)来代替高斯核表示。

(11)

其中：

θ(x;xj;t)=

(12)

然后式(11)可以被写为：

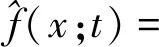
(13)

则：

(14)

n是一个正整数，则：

(15)

式(14)是核密度估计的自适应和替代形式，并且考虑了最佳带宽选择和边界校正。此外，式(14)可以用快速傅里叶变换求解[23]。带宽较小时，式(13)与高斯核相似；而带宽较大时，是一个统一的内核[28]。因此它的性能更优越且与数据的真实密度一致，而式(4)计算得到的密度与真实密度是不一致的。

2.3 最佳带宽自适应选择

Sheather-Jones(SJ)算法[21]曾被用来计算最佳带宽，本文采用改进后的Sheather-Jones算法(The Improved Sheather-Jones)来计算最佳带宽。递归的定点解被看作是带宽的最佳值，并且可以使用快速余弦变换来估计，而不需要考虑分布的正态性假设。利用非线性方程的唯一解可以自适应找到核密度估计的最佳带宽t。

t=ξγ[l](t)

(16)

(17)

*tj=

(18)

ISJ算法的具体流程为：

1)初始化z0=ε，ε是计算精度，n=0；

2)计算zn+1=ξγ[l](zn)(一般l的取值为5)；

3)如果|zn+1-zn|<ε，迭代停止且*t=zn+1；否则n=n+1，重复步骤2);

4)在*t处评估的高斯核密度估计量作为f的最终估计量;*t2=γ[l-1](zn+1)作为‖f″‖的最佳估计带宽。

最佳带宽t对核函数进行规范以获得更准确的估计密度，本文采用t=sqrt(t)/3.3去细化簇的边界。

2.4 本文进行通信辐射源个体识别算法具体步骤

步骤1对信号进行矩形积分双谱变换[14]然后计算直方图特征[30]；

步骤2计算各个信号直方图特征的欧式距离；

步骤3通过式(16)计算带宽t;

步骤4通过式(1)计算ρi，通过式(3)计算δi；

步骤5画出决策图并选择聚类中心；

步骤6给其余非中心点分类，并检查簇的边界点条件；

步骤7输出各信号的类别。

3 实验与分析

3.1 算法在机器学习数据集上的表现

为了验证采用模糊邻域关系比较密度峰值算法的有效性，本文将其与DBSCN算法[31]、OPTICS算法[32]以及DPC算法[20]进行了比较。实验数据集有源于文献[31]中的 Aggregation 数据集、D31 数据集和R15数据集以及来自于UCI机器学习库中的OptdigitsDataset(Optdigits)、Sonar Dataset(Sonar)、the Heart Disease database (Heart)、Wine Recognition Database(Wine)和Iris Plants Database(Iris)。上述数据集的具体说明见表1。

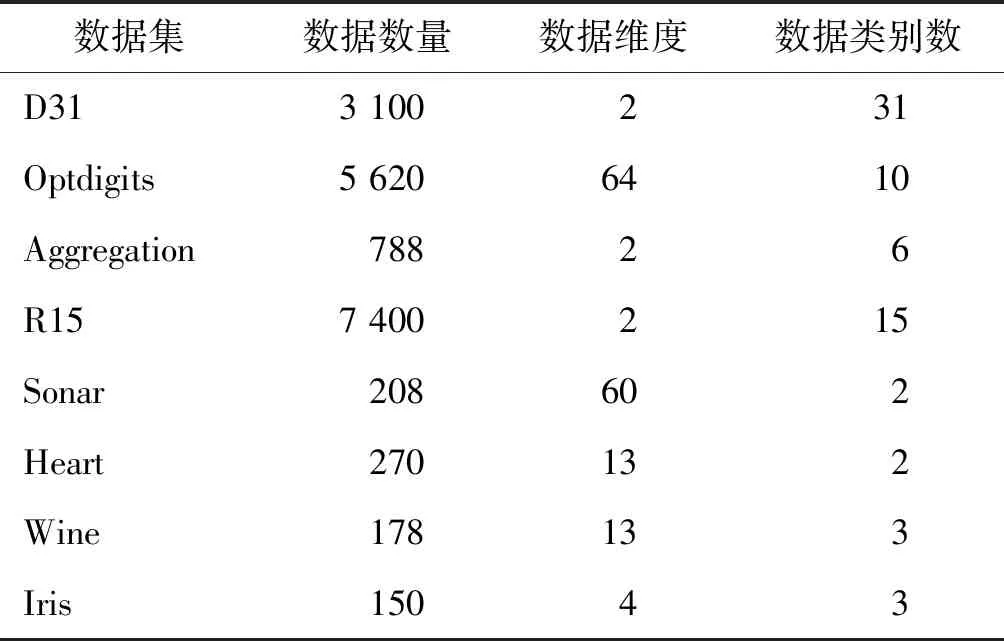
表1 实验数据集描述

表2列出了本文提出的算法和其它算法在8个数据集上的准确率。对于Heart这个数据集，DBSCN算法出现了异常值，因此没有在这个数据集上对DBSCN算法进行评估。从中我们可以看出，DPC-KDE算法能更准确地识别聚类中心点，而不依赖于数据集的性质，而DPC查找密度和边界点的能力在很大程度上取决于数据集的性质。本文提出的DPC-KDE方法是不同数据集聚类的有效通用解决方案。DPC算法的性能很大程度上取决于参数dc的选取，而dc的选取很大程度上依赖于主观经验，这对算法性能的提升是很大的制约，本文提出DPC-KDE算法能够自适应选择最佳参数，在任一数据集上都有较好的表现。

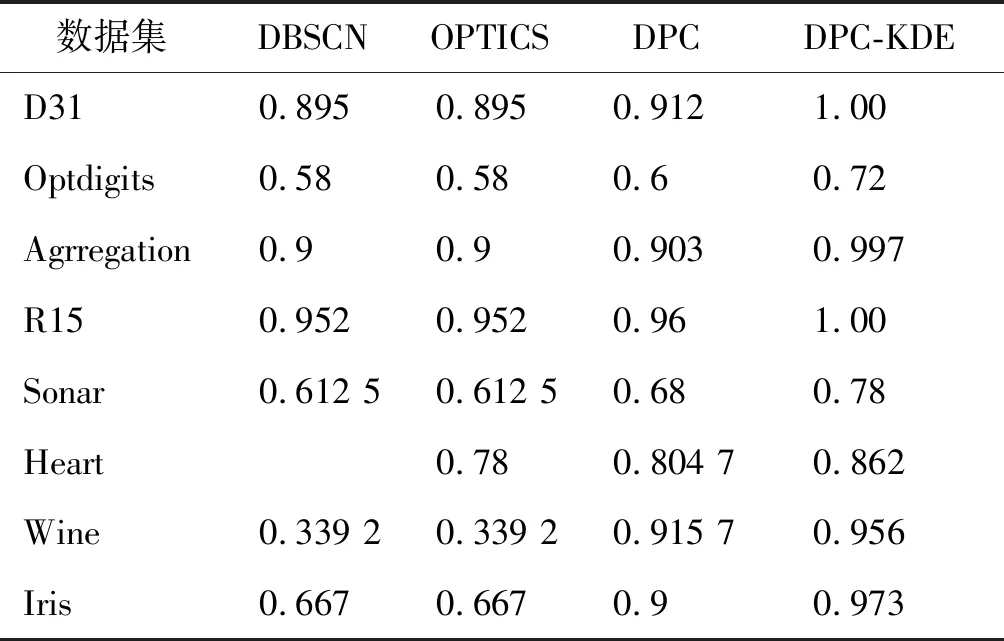
表2 本文算法与其它算法在不同数据集上的对比

3.2 算法在电台信号数据集上的表现

3.2.1 电台信号数据集

为了验证本文提出识别方法的可行性，算法在实际超短波(USW)数据集进行了实验，数据采集场景见图2。课题组采集了5部超短波FM电台不同说话人的语音通信数据。超短波电台信号数据采集时，使用手机播放3个不同的人说话声音作为发射端的输入，然后接收机作为非协作方经过采集获得零中频I/Q信号。背负式超短波FM电台中心频率分别设置为35 MHz、55 MHz和85 MHz，工作模式为“小功率”，并设立了3个采集场景：接收机与电台之间无高大建筑遮挡且距离分别为100 m和50 m，以及接收机与电台中间存在高大建筑物遮挡且距离为50 m，其余参数见表3。信号采集完之后，以2 048个点为单位进行分割，然后分别计算每段信号的直方图特征(特征的维度可以调整)，最后将特征放入算法中进行计算并识别各段信号。

图2 数据采集场景

表3 USW数据集采集接收机参数

3.2.2 特征维度对识别效果的影响

如表4所示，在不同直方图特征维度下进行实验，同其他方法相比，本文方法表现出优异的性能。此外，当直方图特征的维数从128增加到256时，所有方法的识别率都得到显着改善。可以推断出，不同的维度直方图特征包含的信息量不同。特征的维度越高，它们包含的能够区分不同电台信号的信息就越多。

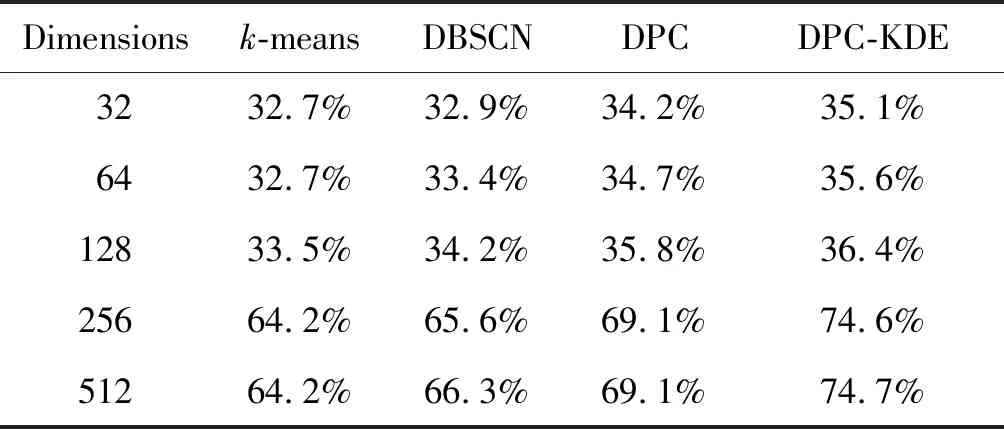
表4 不同特征维度各算法的识别率

3.2.3 信号信噪比(SNR)对识别效果的影响

表5是DPC-KDE，DPC，DBSCN和k-means算法在不同信噪比时的识别率。结果表明，在不同信噪比下，DPC-KDE在识别率方面优于其他聚类方法。它表明信号的信噪比越高，发射机反应在信号的差异越大。

表5 不同信噪比各算法识别率

4 结语

本文将密度峰值算法引入到通信辐射源个体识别中，解决以往全监督或半监督方法在缺乏足够带类别信息的信号样本表现不佳问题，在无监督条件下实现通信辐射源个体识别；针对DPC算法的性能受数据集特性的影响，提出利用核密度估计对数据的内核自适应建模，在不同的数据集上有不同的密度计算方式不同，使估算出的密度更逼近于数据的真实密度；针对DPC算法的参数dc的取值一般由主观经验决定，影响了算法的性能，提出利用热扩散方程中的时间参数t代替带宽h，然后采用ISE算法自适应获得参数的最佳值，进一步提升算法的性能。本文的提出DPC-KDE在实际电台数据集上得到了验证，具有较好的识别效果，在缺乏甚至没有带类别信息的信号样本时，能够发挥重要作用。但本文的方法与以往方法一样，都是在闭集上进行识别，影响其实用性，接下来要结合增量学习，解决通信辐射源个体识别模型的在线学习问题。