最短加法链的算法研究

张仕昌，陈 阳

（1.辽宁工业大学 电气工程学院，辽宁 锦州 121001；2.辽宁工业大学 理学院，辽宁 锦州 121001）

模指数的幂运算是公钥密码学中的核心运算之一，运行效率直接影响着公钥密码体制的执行速度，加法链则能应用到模指数的幂运算中[1]。同时，加法链也被应用到椭圆曲线密码中改进点乘运算的效率[2-4]。加法链相关问题的研究是密码学等相关研究领域中的热门问题[5-6]，下面讨论了计算加法链的2 种算法：二叉树加法链和基于贪心算法的逐步回溯法，并用2 种算法求解了竞赛中提出的第一类和第二类挑战参数的最短加法链。

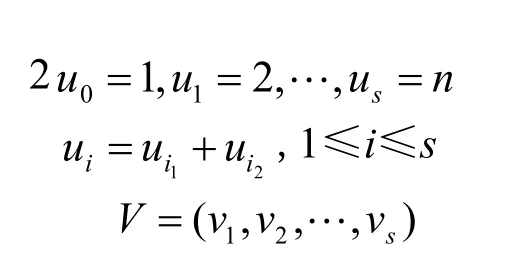
一个长为7的可计算34 的加法链为1-2-4-8-16-32-34。可计算254 的加法链有1-2-4-8-16-32-64-80-84-168-252-254，1-2-4-8-16-32-64-80-84-168-254，1-2-4-8-16-32-48-50-54-100-200-254 等。对于给定的一个数n，可以有几条加法链，找到的可计算n的加法链越短越好。

1 加法链问题

定义1(加法链)正整数n的长度为s的加法链(addition chain)U是一个严格递增的正整数序列满足：

其中：

2 二叉树加法链

定义2星型加法链是一个加法链，且满足。

定义3二叉树加法链，满足：

对于任意正整数n，二叉树加法链算法如下：

例如正整数34 的二叉树加法链(0,2,1,2,1,2)，对应为：

即加法链为1-2-3-4-7-9-16-18-34。

求解密码数学竞赛中第二类挑战问题参数：n=211108170305887，得到加法链长度为59，最短加法链为 1-2-3-4-8-16-32-64-128-256-512-1024-2048-4096-8192-16384-32768-65536-131072-262144-524288-1048576-2097152-4194304-8388608-16777 216-33554432-67108864-134217728-268435456-536 870912-1073741824-2147483648-4294967296-85899 34592-17179869184-34359738368-68719476736-137 438953472-274877906944-549755813888-10995116 27776-2199023255552-4398046511104-87960930222 08-17592186044416-35184372088832-70368744177 664-140737488355328-211106232532992-211107306 274816-211107843145728-211108111581184-211108 145135616-211108161912832-211108170301440-211 108170305536-211108170305792-211108170305856-211108170305888。

3 基于贪心算法的逐步回溯法

贪心算法(greedy algorithm)是一种算法技术，总是做出在当前来说是最好的选择，而并不从整体上加以考虑，所做出的每步选择只是当前步骤的局部最优选择。

对于最短加法链问题，目标是尽快找到正整数n，利用贪心算法，每一次都把当前值的2 倍作为下一个值，如果超过目标正整数n，则使用当前的最大值与次大值之和作为下一个值，具体操作如下。

从1 开始出发，将1 加入数组list中，当前下标为index、值为list[index]=k，每次生成新的值下标为index+1，值为k+k,即list[index+1]=k+k,当k+k＞目标正整数n时，则进行list的向前遍历，使得k+list[index-i]＜n(i=0,…,index)，并将新值添加到list中，直至得到目标正整数n。这样得到一个加法链的初始解。

深度优先搜索算法(DFS)是树的先根遍历的推广，每个节点仅访问1 次且对每一个可能的分支路径深入到不能再深入为止。把贪心算法得到加法链的初始解的深度设为全局上界GUB，利用深度优先搜索算法进一步优化这个可行解，若搜索深度1 超过贪心算法得到的深度，即1＞GUB，停止搜索，然后返回到上一个节点或继续返回上一个节点进行搜索。当前节点值为t，当前层次为l，通过贪心算法得到的层次为L，目标正整数为n，通过数学归纳法得＜n或L＜log2n/t+l，就对其进行剪枝[7]，使其减少空间和运行时间，能更快得到较好的解。

对于第二类挑战问题参数n=10445360463911，通过贪心算法得到一个可行解，得到加法链的长度为49，对其数据进行分析，再使用深度优先搜索算法时，对前40 层的节点值进行确定，并使用剪枝函数，得到加法链长度为46。