关于有毒气体扩散问题的预估模型

金雪莲

（辽宁工业大学 理学院，辽宁 锦州 121001）

1 问题的提出

当发生有毒气体突发性泄露事故时，有关部门需要快速对泄漏源进行定位和识别，并科学预测有毒气体的蔓延及影响范围。其中，分析有毒气体在大气中的扩散是泄露事故后果分析的重要内容，其目的在于定量地描述泄漏事故对人员和环境造成伤害的程度，并预测危害后果。2010年，一辆装载环氧乙烷的运输车辆在某国道上侧翻，造成有毒气体外泄。虽经消防人员紧急处置，在等待救援和处置过程中，仍有大约1 000 个单位质量的环氧乙烷气体扩散到周边区域。为了分析泄露事故可能引发的后果，在以事发点为中心东西南北各3 km、高度150 m 范围的空间区域中，监测部门对毒物的浓度进行了抽样测量(见表1)。由于公路北侧是农田而南侧是绿化林带，可能导致公路南北两侧的污染程度有一定差异，因此抽样测量分为2 个部分进行，其中前3 列为取样点的坐标，第4 列为取样点处毒物的浓度。

表1 2 个地区毒气浓度的抽样结果

2 基本假设

假设1有毒气体释放瞬间是向各个方向等强度释放的。

假设2气体在整个扩散过程中不考虑温度、风速、风向、热传递、热辐射的因素。

假设3气体在整个扩散过程中遵守理想气体状态方程。

假设4气体的扩散服从扩散定律。

假设5遵守质量守恒定律。

3 模型建立

3.1 有毒气体浓度的变化规律

建立空间直角坐标系，将毒气泄漏瞬间记作t=0，泄漏点选为坐标原点，根据假设4，每秒通过法向面积为1 m2的流量为：

其中：grad 表示梯度；σ表示气体的扩散系数；q表示毒气的流量；负号表示气体的扩散方向是从浓度高的地方向浓度低的方向扩散。

图1 为模型的理想化图形。

图1 模型的理想化图形

当时间间隔为Δt时，通过毒气域Ω的流量为：

其中：Q释放出有毒气体的总量；S表示包围毒气域所形成的空间曲面；n包围毒气域所形成的空间曲面的法向量。

时间间隔为Δt时，毒气域Ω内气体的增量为：

其中：C(x,y,z,t)表示t时刻气体在任意一点处的浓度。

由假设5 可知：

由高斯公式可以得到：

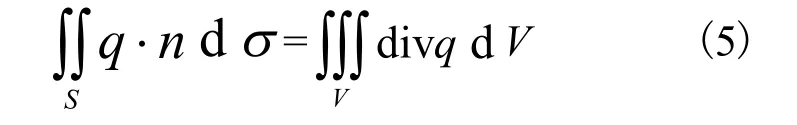
其中：div 为散度。

由积分中值定理得：

根据假设1，在t=0 时刻气体泄漏点处的气体浓度为：

其中δ(x,y,z)表示点源函数，由(7)可以解得偏微分方程(6)的解为：

这样就计算出气体在任意时刻、任意点的浓度，从结果中可以看出有毒气体浓度C的等值面是以泄漏点为球心的球面上，并且球的半径越大，浓度值越小。

4 模型的求解

对上节建立的模型使用MATLAB 程序进行求解，对于数据1，由于该组数据是在某一时刻对不同数据点测量的浓度值，因此时间t可以取为常数1。毒气总量为1 000 个单位，利用该组数据可对扩散系数进行拟合，得到区域1 的扩散系数为1.6。对于第二组数据，利用同样的方法可得其扩散系数为0.75。将其分别带入到模型当中得到：

农田毒气扩散模型

绿化带毒气扩散模型

下面分别对这2 种扩散模型进行MATLAB 仿真，并对仿真结果进行分析。

4.1 农田毒气浓度图形分析

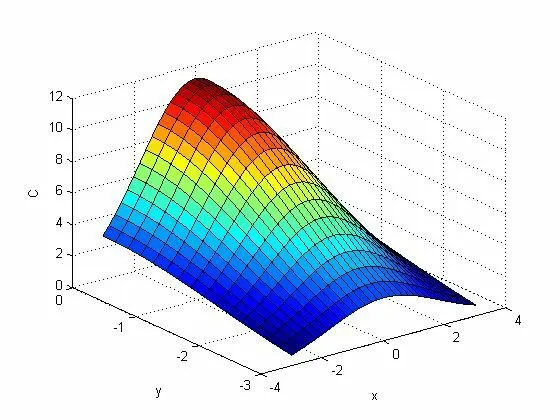
图2 第1 h 农田高度为0 m 即地表毒气浓度扩散图

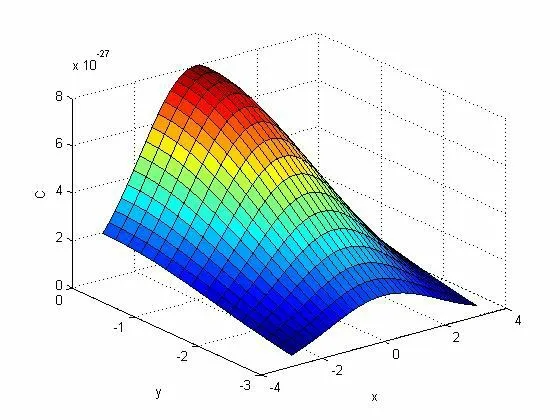
图3 第1 h 农田高度为20 m 毒气浓度扩散图

图4 第12 h 农田高度为0 m 即地表毒气浓度扩散图

图5 第12 h 农田高度为20 m 毒气浓度扩散图

从图2～图5 分析来看：(1)在固定时间内随着高度的增加毒气浓度降低，从整个区域看，周边区域的毒气浓度是呈现降低趋势的。(2)12 h 后，地表毒气浓度明显降低，同一高度的浓度虽然有所增加，但是总体浓度已经明显降低小于0.28。(3)12 h后，毒气范围缩小。

4.2 绿化带毒气浓度图形分析

从图6～图9 分析看：(1)在固定时间内随着高度的增加毒气浓度降低，从整个区域看，周边区域的毒气浓度是呈现降低趋势的。(2)12 h 后，地表毒气浓度明显降低，同一高度的浓度虽然有所增加，但是总体浓度已经明显降低小于0.9。(3)12 h后，毒气范围缩小。

经比较分析发现，绿化带区域经过12 h 后与农田区域进行比较，农田区域的毒气浓度降低得更快。

5 结束语

图6 第1 h 绿化带高度为0 m 即地表毒气浓度扩散图

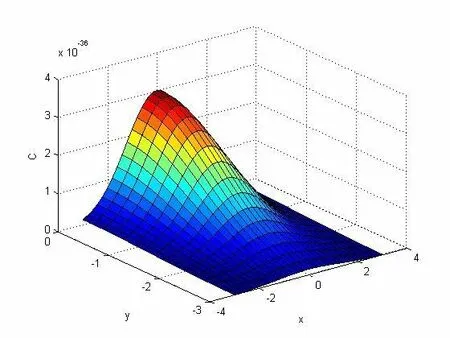
图7 第1 h 绿化带高度为20 m 毒气浓度扩散图

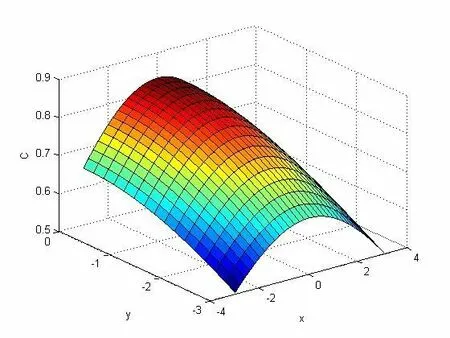
图8 第12 h 绿化带高度为0 m 即地表毒气浓度扩散图

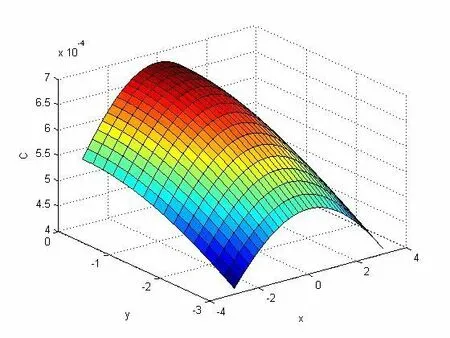
图9 第12 h 绿化带高度为20 m 毒气浓度扩散图

比较农田和绿化带2 种不同区域的毒气扩散程度可以看出，尽管2 种植被均有净化作用，但农田域毒气浓度降低得更快。尽管如此毒气扩散的程度和植被的空间体积也存在明显关系，与风速、风向等外界条件也有关系，所以本文还是有一定局限性，仍然需要进一步研究。